Three 20 resistors, A, B and C are connected as shown in figure.

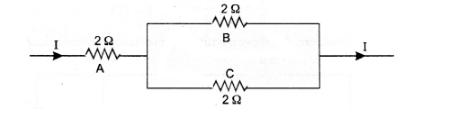
Here, $P=18 W$

Using, $P=I^{2} R$, we get

$I=\sqrt{\frac{\mathrm{P}}{\mathrm{R}}}=\sqrt{\frac{18}{2}}=\sqrt{9}=3 \mathrm{~A}$

$\therefore$ Maximum current that can flow through a resistor $A=3 A$

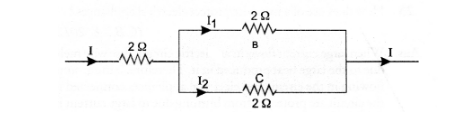
Since resistors B and C are connected in parallel, so potential difference across B and C is same. Let I1, be the current flowing through resistor.B

and I2 be the current flowing through resistor C

$\therefore$ $\mathrm{I}_{1} \mathrm{R}_{1}=\mathrm{I}_{2} \mathrm{R}_{2}$ or $\frac{\mathrm{I}_{1}}{\mathrm{I}_{2}}=\frac{\mathrm{R}_{2}}{\mathrm{R}_{1}}=\frac{2 \Omega}{2 \Omega}=1$

$\begin{array}{ll}\text { or } \mathrm{I}_{1} & =\mathrm{I}_{2}\end{array}$

But $\quad \mathrm{I}_{1}+\mathrm{I}_{2}=\mathrm{I}=3$

$\therefore \quad 2 \mathrm{I}_{1}=3$ or $\mathrm{I}_{1}=1.5 \mathrm{~A}$

and $\quad \mathrm{I}_{2}=\mathrm{I}_{1}=1.5 \mathrm{~A}$