Three circles are placed on a plane in such a way that each circle

Let there be 3 circles with centre A, B and C respectively such that each circle touches the other two. They all have radius of 10 cm.

We have to find the area enclosed between the circles.

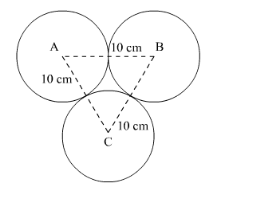
We have,

$\mathrm{AB}=10 \mathrm{~cm}$

$\mathrm{BC}=10 \mathrm{~cm}$

$\mathrm{CA}=10 \mathrm{~cm}$

$A B=10+10 \mathrm{~cm}=20 \mathrm{~cm}$

$B C=10+10 \mathrm{~cm}=20 \mathrm{~cm}$

$C A=10+10 \mathrm{~cm}=20 \mathrm{~cm}$

Hence $\triangle \mathrm{ABC}$ is an equilateral triangle.

So, $\angle \mathrm{ABC}=60^{\circ}, \angle \mathrm{BCA}=60^{\circ} \angle \mathrm{CAB}=60^{\circ}$

So, the area enclosed between the circles,

Required area $=\operatorname{ar}(\triangle \mathrm{ABC})-3($ Area of the sector formed $)$

So,

Required area $=\frac{\sqrt{3}}{4}(\mathrm{AB})^{2}-3\left(\frac{1}{2}(r)^{2} \frac{\theta}{180} \pi\right)$

Put the values to get,

Required area $=\frac{\sqrt{3}}{4}(20)^{2}-3\left(\frac{1}{2}(10)^{2} \frac{60}{180}\left(\frac{22}{7}\right)\right)$

$=173.2-3(52.38)$

$=(173.2-157.14) \mathrm{cm}^{2}$

$=16.05 \mathrm{~cm}^{2}$