Question:
Three letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the envelopes at random so that each envelope contains exactly one letter. Find the probability that at least one letter is in its proper envelope.
Solution:
Let $L_{1}, L_{2}, L_{3}$ be three letters and $E_{1}, E_{2}$, and $E_{3}$ be their corresponding envelops respectively.
There are 6 ways of inserting 3 letters in 3 envelops. These are as follows:
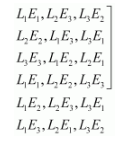
There are 4 ways in which at least one letter is inserted in a proper envelope.
Thus, the required probability is $\frac{4}{6}=\frac{2}{3}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
