To construct a triangle similar to $\triangle \mathrm{ABC}$ in which $\mathrm{BC}=4.5 \mathrm{~cm}, \angle \mathrm{B}=45^{\circ}$ and $\angle \mathrm{C}=60^{\circ}$, using a scale factor of $\frac{3}{7}, \mathrm{BC}$ will be divided in the ratio
(a) $3: 4$
(b) $4: 7$
(c) $3: 10$
(d) $3: 7$
To construct a triangle similar to $\triangle \mathrm{ABC}$ in which $\mathrm{BC}=4.5 \mathrm{~cm}, \angle \mathrm{B}=45^{\circ}$ and $\angle \mathrm{C}=60^{\circ}$, using a scale factor of $\frac{3}{7}, \mathrm{BC}$ will be divided in the ratio $3: 4$.
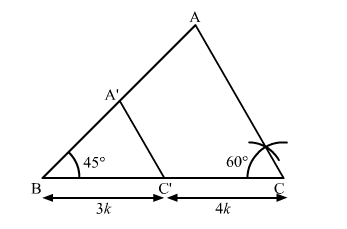
Here, ∆ABC ∼ ∆A'BC'
BC' : C'C = 3 : 4
or BC' : BC = 3 : 7
Hence, the correct answer is option A.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
