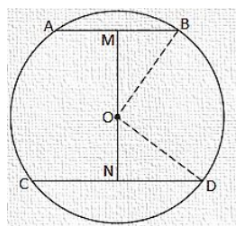
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are

Draw OM⊥AB and ON⊥CD.

Join OB and OD.

BM = AB/2 = 5/2 [Perpendicular from the centre bisects the chord]

ND = CD/2 = 11/2

Let ON be x, so OM will be 6 - x.

ΔMOB

$\mathrm{OM}^{2}+\mathrm{MB}^{2}=\mathrm{OB}^{2}$

$(6-x)^{2}+(5 / 2)^{2}=O B^{2}$

$36+x^{2}-12 x+25 / 4=O B^{2} \ldots$ (i)

In ΔNOD

$O N^{2}+N D^{2}=O D^{2}$

$x^{2}+(11 / 2)^{2}=0 D^{2}$

$x^{2}+121 / 2=O D^{2} \ldots \ldots$ (ii)

We have OB = OD. [Radii of same circle]

So, from equation (i) and (ii).

$36+x^{2}-12 x+25 / 4=x^{2}+121 / 2$

$\Rightarrow 12 x=36+25 / 4-121 / 4$

$=\frac{144+25-121}{4}$

$=\frac{48}{4}=12$

x = 1

From equation (ii)

$(1)^{2}+(121 / 4)=\mathrm{OD}^{2}$

$O D^{2}=1+121 / 4=125 / 4$

$O D=\frac{5 \sqrt{5}}{2}$

So, the radius of the circle is found to be $55 \sqrt{2} \mathrm{~cm}$