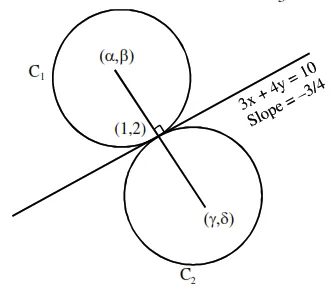
Two circles each of radius 5 units touch each other at the point $(1,2)$. If the equation of their common tangent is $4 \mathrm{x}+3 \mathrm{y}=10$, and $\mathrm{C}_{1}(\alpha, \beta)$ and $\mathrm{C}_{2}(\gamma, \delta)$, $\mathrm{C}_{1} \neq \mathrm{C}_{2}$ are their centres, then $|(\alpha+\beta)(\gamma+\delta)|$ is equal to
Slope of line joining centres of circles $=\frac{4}{3}=\tan \theta$
$\Rightarrow \cos \theta=\frac{3}{5}, \sin \theta=\frac{4}{5}$
Now using parametric form
$\frac{x-1}{\cos \theta}=\frac{y-2}{\sin \theta}=\pm 5$
$\oplus(\mathrm{x}, \mathrm{y})=(1+5 \cos \theta, 2+5 \sin \theta)$
$(\alpha, \beta)=(4,6)$
$\Theta \quad(x, y)=(\gamma, \delta)=(1-5 \cos \theta, 2-5 \sin \theta)$
$(\gamma, s)=(-2,-2)$
$\Rightarrow|(\alpha+\beta)(\gamma+\delta)|=|10 x-4|=40$
