Two circles with centres 0 and 0′ of radii 3 cm and 4 cm,

Here, two circles are of radii OP = 3 cm and PO’ = 4 cm

These two circles intersect at P and Q.

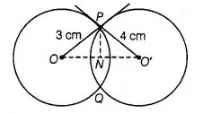
Here, $O P$ and $P O^{\prime}$ are two tangents drawn at point $P$.

$\angle O P O^{\prime}=90^{\circ}$

[tangent at any point of circle is perpendicular to radius through the point of contact]

Join $O O^{\prime}$ and $P N$.

In right angled $\triangle O P O^{\prime}$,

$\left(O O^{\prime}\right)^{2}=(O P)^{2}+\left(P O^{\prime}\right)^{2}$ [by Pythagoras theorem]

i.e., $\quad(\text { Hypotenuse })^{2}=(\text { Base })^{2}+(\text { Perpendicular })^{2}$

$=(3)^{2}+(4)^{2}=25$

$O O^{\prime}=5 \mathrm{~cm}$

Aso, $P N \perp O O^{\prime}$

Let $O N=x$, then $N O^{\prime}=5-x$

In right angled $\triangle O P N$,

$(O P)^{2}=(O N)^{2}+(N P)^{2} \quad$ [by Pythagoras theorem]

$\Rightarrow$ $(N P)^{2}=3^{2}-x^{2}=9-x^{2}$ $\ldots$ (i)

and in right angled $\triangle P N O^{\prime}$,

$\left(P O^{\prime}\right)^{2}=(P N)^{2}+\left(N O^{\prime}\right)^{2}$  [by Pythagoras theorem]

$\Rightarrow \quad(4)^{2}=(P N)^{2}+(5-x)^{2}$

$\Rightarrow \quad(P N)^{2}=16-(5-x)^{2}$ .....(ii)

From Eqs. (i) and (ii), 

$9-x^{2}=16-(5-x)^{2}$

$\Rightarrow \quad 7+x^{2}-\left(25+x^{2}-10 x\right)=0$

$\Rightarrow \quad 10 x=18$

$\therefore$$x=1.8$ 

Again, in right angled $\triangle O P N$,

$O P^{2}=(O N)^{2}+(N P)^{2}$ [by Pythagoras theorem]

$\Rightarrow \quad 3^{2}=(1.8)^{2}+(N P)^{2}$

$\Rightarrow \quad(N P)^{2}=9-3.24=5.76$

$\therefore$$(N P)=2.4$ 

$\therefore$ Length of common chord, $P Q=2 P N=2 \times 2.4=4.8 \mathrm{~cm}$