Two circles with centres O and O' intersect at two points A and B. A line PQ is drawn parallel to OO' through A or B, intersecting the circles at P and Q.

Given: Two circles with centres O and O' intersect at two points A and B.

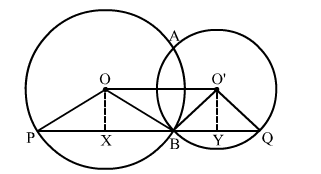
Draw a line PQ parallel to OO' through B, OX perpendicular to PQ, O'Y perpendicular to PQ, join all.

We know that perpendicular drawn from the centre to the chord, bisects the chord.

∴ PX = XB and YQ = BY

∴ PX + YQ = XB + BY

On adding XB + BY on both sides, we get

PX + YQ + XB + BY = 2(XB + BY)
⇒ PQ = 2(XY)
⇒ PQ = 2(OO')

Hence, PQ = 2OO'.