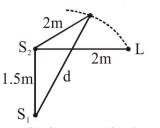
Two coherent sources of sound, $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$, produce sound waves of the same wavelength, $\lambda=1 \mathrm{~m}$, in phase. $S_{1}$ and $S_{2}$ are placed $1.5 \mathrm{~m}$ apart (see fig.) A listener, located at $\mathrm{L}$, directly in front of $\mathrm{S}_{2}$ finds that the intensity is at a minimum when he is $2 \mathrm{~m}$ away from $\mathrm{S}_{2}$. The listener moves away from $S_{1}$, keeping his distance from $S_{2}$ fixed. The adjacent maximum of intensity is observed when the listener is at a distance $d$ from $S_{1}$. Then, $d$ is :
Correct Option: 2,
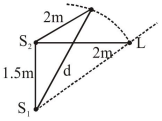
Initially $S_{2} L=2 m$
$S_{1} L=\sqrt{2^{2}+(3 / 2)^{2}}$
$\mathrm{S}_{1} \mathrm{~L}=\frac{5}{2}=2.5 \mathrm{~m}$
$\Delta \mathrm{x}=\mathrm{S}_{1} \mathrm{~L}-\mathrm{S}_{2} \mathrm{~L}=0.5 \mathrm{~m}$
So since $\lambda=1 \mathrm{~m} \quad \therefore \Delta x=\frac{\lambda}{2}$
So while listener moves away from $S_{1}$
Then, $\Delta x\left(=S_{1} L-S_{2} L\right)$ increases
and hence, at $\Delta x=\lambda$ first maxima will appear.
$\Delta x=\lambda=S_{1} L-S_{2} L$
$1=\mathrm{d}-2 \Rightarrow \mathrm{d}=3 \mathrm{~m}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
