Two cones with same base radius 8 cm

If two cones with same base and height are joined together along their bases, then the shape so formed is look like as figure shown.

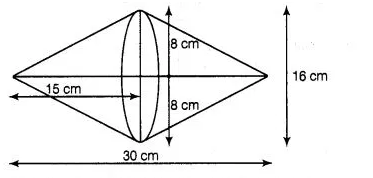
Given that, radius of cone, $r=8 \mathrm{~cm}$ and height of cone, $h=15 \mathrm{~cm}$

So, surface area of the shape so formed

$=$ Curved area of first cone + Curved surface area of second cone

$=2$. Surface area of cone

[since, both cones are identical]

$=2 \times \pi l=2 \times \pi \times r \times \sqrt{r^{2}+h^{2}}$

$=2 \times \frac{22}{7} \times 8 \times \sqrt{(8)^{2}+(15)^{2}}$

$=\frac{2 \times 22 \times 8 \times \sqrt{64+225}}{7}$

$=\frac{44 \times 8 \times \sqrt{289}}{7}$

$=\frac{44 \times 8 \times 17}{7}$

$=\frac{5984}{7}=854.85 \mathrm{~cm}^{2}$

$=855 \mathrm{~cm}^{2}$ (approx)

Hence, the surface area of shape so formed is 855 cm²