Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'.
Question:
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle '' with the vertical ?
Correct Option: , 2
Solution:
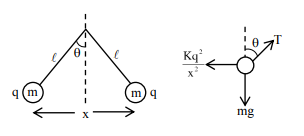
$\mathrm{T} \cos \theta=\mathrm{mg}$
$\mathrm{T} \sin \theta=\frac{\mathrm{kq}^{2}}{\mathrm{x}^{2}}$
$\tan \theta=\frac{k q^{2}}{x^{2} m g}$
as $\tan \theta \approx \sin \theta \approx \frac{x}{2 L}$
$\frac{\mathrm{x}}{2 \mathrm{~L}}=\frac{\mathrm{Kq}^{2}}{\mathrm{x}^{2} \mathrm{mg}}$
$x=\left(\frac{q^{2} L}{2 \pi \varepsilon_{0} m g}\right)^{1 / 3}$