Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
(a) 4 : 5
(b) 5 : 4
(c) 3 : 2
(d) 5 : 7
Given: Two isosceles triangles have equal vertical angles and their areas are in the ratio of 16:25.
To find: Ratio of their corresponding heights.
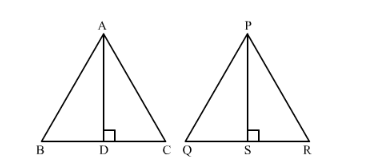
Let ∆ABC and ∆PQR be two isosceles triangles such that ∠A=∠P. Suppose AD ⊥ BC and PS ⊥ QR .
In ∆ABC and ∆PQR,
ABPQ=ACPR∠A=∠P∴∆ABC~∆PQR SAS similarity
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Hence,
Ar∆ABCAr∆PQR=ADPS2⇒1625=ADPS2⇒ADPS=45
Hence we got the result as $(a)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
