Two line segments AB and AC

Solution:

Given that, AB = 5 cm and AC = 7 cm

Also, $A P=\frac{3}{4} A B$ and $A Q=\frac{1}{4} A C$ ...(i)

From Eq. (i), $A P=\frac{3}{4} \cdot A B=\frac{3}{4} \times 5=\frac{15}{4} \mathrm{~cm}$

Than, $P B=A B-A P=5-\frac{15}{4}=\frac{20-15}{4}=\frac{5}{4} \mathrm{~cm}$ $[\because P$ is any point on the $A B]$

$\therefore$ $A P: P E=\frac{15}{4}: \frac{5}{4} \Rightarrow A P: P B=3: 1$

i.e., scale factor of line segment $A B$ is $\frac{3}{1}$,

Again from Eq. (i), $\quad A Q=\frac{1}{4} A C=\frac{1}{4} \times 7=\frac{7}{4} \mathrm{~cm}$

Then, $Q C=A C-A Q=7-\frac{7}{4}$

$=\frac{28-7}{4}=\frac{21}{4} \mathrm{~cm}$ $[\because Q$ is any point on the $A C]$

$\therefore \quad A Q: Q C=\frac{7}{4}: \frac{21}{4}=1: 3$ 

$\Rightarrow \quad A Q: Q C=1: 3$

i.e., scale factor of line segment $A Q$ is $\frac{1}{3}$.

Steps of construction

1. Draw a line segment AB = 5 cm.
2. Now draw a ray AZ making an acute ∠BAZ = 60°.
3. With A as centre and radius equal to 7 cm draw an arc cutting the line AZ at C.
4. Draw a ray AX, making an acute ∠BAX
5. Along AX, mark 1+3 = 4 points A1, A2, A3, and A4 Such that AA1 = A1A2 = A2A3 = A3A4
6. Join A4B
7. From A3 draw A3P || A4B meeting AB at  P                   [by making an angle equal to ∠AA4B]
   Then, Pis the point on AB which divides it in the ratio 3:1.
   So,                                        AP: PB = 3:1
8. Draw a ray AY, making an acute  ∠CAY

9. Along AY, mark $3+1=4$ points $B_{1}, B_{2}, B_{3}$ and $B_{4}$.

Such that $\mathrm{AB}_{1}=\mathrm{B}_{1} \mathrm{~B}_{2}=\mathrm{B}_{2} \mathrm{~B}_{3}=\mathrm{B}_{3} \mathrm{~B}_{4}$

10. Join $\mathrm{B}_{4} \mathrm{C}$

11. From $B_{1}$ draw $B_{1} Q \| B_{4} C$ meeting $A C$ atQ. [by making an angle equal to $\angle A B_{4} C$ ]

Then, $Q$ is the point on $A C$ which divides it in the ratio $1: 3$.

So $\mathrm{AQ}: \mathrm{OC}=1: 3$

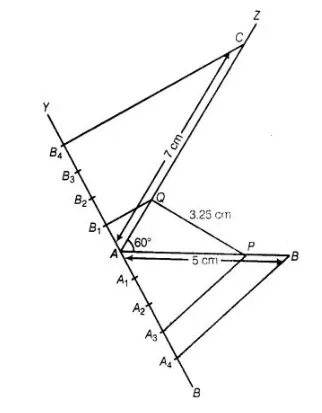
12. Finally, join PQ and its measurment is $3.25 \mathrm{~cm}$.