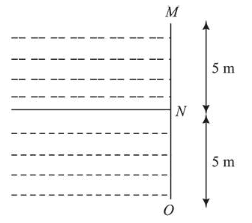
Two liquids of densities $\rho_{1}$ and $\rho_{2}\left(\rho_{2}=2 \rho_{1}\right)$ are filled up behind a square wall of side $10 \mathrm{~m}$ as shown in figure. Each liquid has a height of $5 \mathrm{~m}$. The ratio of the forces due to these liquids exerted on upper part $M N$ to that at the lower part $N O$ is (Assume that the liquids are not mixing):
Correct Option: , 4
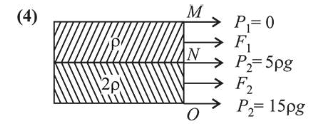
Let $P_{1}, P_{2}$ and $P_{3}$ be the pressure at points $M, N$ and
$O$ respectively.
Pressure is given by $P=\rho g h$ Now, $P_{1}=0(\because h=0)$
Now, $P_{1}=0(\because h=0)$
$P_{2}=\rho g(5)$
$P_{3}=\rho g(15)$
$\quad=15 \rho g$
Force on upper part, $F_{1}=\frac{\left(P_{1}+P_{2}\right)}{2} A$
Force on lower part, $F_{2}=\frac{\left(P_{2}+P_{3}\right)}{2} A$
$\therefore \frac{F_{1}}{F_{2}}=\frac{5 \rho g}{20 \rho g}=\frac{5}{20}=\frac{1}{4}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.