Two men are on opposite sides of a tower. they measure the angles of elevation of the top of the tower as 30° and 45° respectively.

Let $C D$ be the tower and $A$ and $B$ be the positions of the two men standing on the opposite sides. Thus, we have:

$\angle D A C=30^{\circ}, \angle D B C=45^{\circ}$ and $C D=50 \mathrm{~m}$

Let $A B=x \mathrm{~m}$ and $B C=y \mathrm{~m}$ such that $A C=(x-y) \mathrm{m}$.

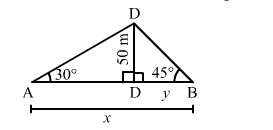
In the right $\Delta D B C$. we have:

$\frac{C D}{B C}=\tan 45^{\circ}=1$

$\Rightarrow \frac{50}{y}=1$

$\Rightarrow y=50 \mathrm{~m}$

In the right $\triangle A C D$, we have:

$\frac{C D}{A C}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}$

$\Rightarrow \frac{50}{(x-y)}=\frac{1}{\sqrt{3}}$

$\Rightarrow x-y=50 \sqrt{3}$

On putting $y=50$ in the above equation, we get:

$x-50=50 \sqrt{3}$

$\Rightarrow x=50+50 \sqrt{3}=50(\sqrt{3}+1)=136.6 \mathrm{~m}$

$\therefore$ Distance between the two men $=A B=x=136.6 \mathrm{~m}$