Two numbers are selected at random (without replacement) from the first six positive integers.

The two positive integers can be selected from the first six positive integers without replacement in 6 × 5 = 30 ways

X represents the larger of the two numbers obtained. Therefore, X can take the value of 2, 3, 4, 5, or 6.

For X = 2, the possible observations are (1, 2) and (2, 1).

$\therefore \mathrm{P}(\mathrm{X}=2)=\frac{2}{30}=\frac{1}{15}$\

For X = 3, the possible observations are (1, 3), (2, 3), (3, 1), and (3, 2).

$\therefore \mathrm{P}(\mathrm{X}=3)=\frac{4}{30}=\frac{2}{15}$

For $X=4$, the possible observations are $(1,4),(2,4),(3,4),(4,3),(4,2)$, and $(4,1)$.

$\therefore \mathrm{P}(\mathrm{X}=4)=\frac{6}{30}=\frac{1}{5}$

For $X=5$, the possible observations are $(1,5),(2,5),(3,5),(4,5),(5,4),(5,3),(5,2)$, and $(5,1)$.

$\therefore \mathrm{P}(\mathrm{X}=5)=\frac{8}{30}=\frac{4}{15}$

For $X=6$, the possible observations are $(1,6),(2,6),(3,6),(4,6),(5,6),(6,5),(6,4),(6,3),(6,2)$, and $(6,1)$.

$\therefore \mathrm{P}(\mathrm{X}=6)=\frac{10}{30}=\frac{1}{3}$

Therefore, the required probability distribution is as follows.

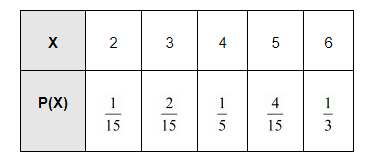
Then, $\mathrm{E}(\mathrm{X})=\sum \mathrm{X}_{i} \mathrm{P}\left(\mathrm{X}_{i}\right)$

$=2 \cdot \frac{1}{15}+3 \cdot \frac{2}{15}+4 \cdot \frac{1}{5}+5 \cdot \frac{4}{15}+6 \cdot \frac{1}{3}$

$=\frac{2}{15}+\frac{2}{5}+\frac{4}{5}+\frac{4}{3}+2$

$=\frac{70}{15}$

$=\frac{14}{3}$