Two parallel sides of a trapezium are 60 m and 77 m and the other sides are 25 m and 26 m. Find the area of the trapezium?

Given,

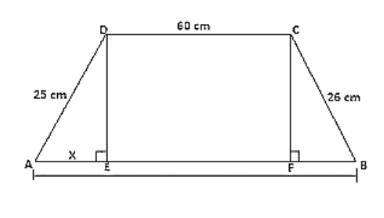
Two parallel sides of trapezium are AB = 77 m and CD = 60 m

The other two parallel sides of trapezium are BC = 26 m, AD = 25m

Join AE and CF

DE is perpendicular to AB and also, CF is perpendicular to AB

Therefore, DC = EF = 60 m

Let AE = x

So, BF = 77 - 60 - x

BF = 17 - x

In triangle ADE,

By using Pythagoras theorem,

$\mathrm{DE}^{2}=\mathrm{AD}^{2}-\mathrm{AE}^{2}$

$\mathrm{DE}^{2}=25^{2}-\mathrm{x}^{2}$

In triangle BCF,

By using Pythagoras theorem,

$C F^{2}=B C^{2}-B F^{2}$

$C F^{2}=26^{2}-(17-x)^{2}$

Here, DE = CF

So. $D E^{2}=C F^{2}$

$25^{2}-x^{2}=26^{2}-(17-x)^{2}$

$25^{2}-x^{2}=26^{2}-\left(17^{2}-34 x+x^{2}\right)$

$25^{2}-x^{2}=26^{2}-17^{2}+34 x+x^{2}$

$25^{2}=26^{2}-17^{2}+34 x$

$x=7$

$\mathrm{DE}^{2}=25^{2}-\mathrm{x}^{2}$

$\mathrm{DE}=\sqrt{625-49}$

DE = 24 m

Area of trapezium = 1/2 × (60 + 77) × 24

Area of trapezium $=1644 \mathrm{~m}^{2}$