Two poles are 'a' metres apart and the height of one is double of the other.

Let AB and CD be the two posts such that AB < CD.

Then, let AB = h so that CD = 2h

Now, the given information can be represented as,

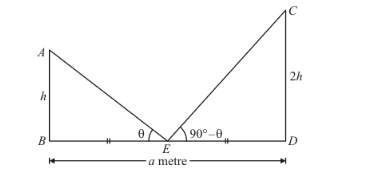
Here, E is the midpoint of BD.

We have to find height of the shorter post.

So we use trigonometric ratios.

In triangle ECD,

$\tan \angle C E D=\frac{C D}{E D}$

$\Rightarrow \tan \left(90^{\circ}-\theta\right)=\frac{2 h}{\left(\frac{a}{2}\right)}$

$\Rightarrow \cot \theta=\frac{4 h}{a}$ ........(1)

Again in triangle ABE,

$\Rightarrow \tan \angle A E B=\frac{A B}{B E}$

$\Rightarrow \tan \theta=\frac{h}{\left(\frac{a}{2}\right)}$

$\Rightarrow \frac{1}{\cot \theta}=\frac{2 h}{a}$

$\Rightarrow \frac{a}{4 h}=\frac{2 h}{a}$

$\Rightarrow a^{2}=8 h^{2}$

$\Rightarrow h=\frac{a}{2 \sqrt{2}}$

Hence the correct option is $b$.