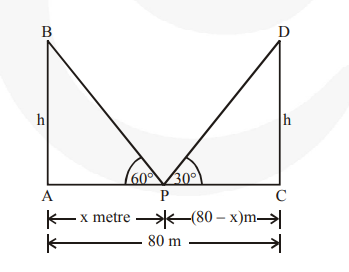
Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide.

Let AB and CD be the towels & P is the point between them. 

AB = h metres

CD = h metres

AP = x m

CP = (80 – x) m 

Now, in right $\triangle \mathrm{APB}$, We have

$\frac{\mathbf{A B}}{\mathbf{A P}}=\tan 60^{\circ}$

$\frac{\mathbf{h}}{\mathbf{x}}=\sqrt{\mathbf{3}}$

$\Rightarrow \mathrm{h}=\mathrm{x} \sqrt{\mathbf{3}}$  ..(1)

Again in right $\Delta \mathrm{CPD}$, we have

$\frac{\text { CD }}{\text { CP }}=\tan 30^{\circ}$

$\Rightarrow \frac{h}{(80-x)}=\frac{1}{\sqrt{3}}$

$\Rightarrow \mathrm{h}=\frac{\mathbf{8 0}-\mathbf{x}}{\sqrt{\mathbf{3}}}$  ...(2)

From (1) and (2), we get

$\sqrt{3} x=\frac{80-x}{\sqrt{3}}$

$\Rightarrow \sqrt{\mathbf{3}} \times \sqrt{\mathbf{3}} \times x=80-x$

$\Rightarrow 3 x=80-x$

$\Rightarrow 3 x+x=80=$

$4 x=80$

$x=\frac{80}{4}=20$

$\therefore \quad C P=80-x=80-20=60 \mathrm{~m}$

Now, from (1), we have

$h=\sqrt{\mathbf{3}} \times 20=1.732 \times 20=34.64$

Thus, the required point is 20 m away from the first pole and 60 m away from the second pole.

Height of each pole = 34.64 m.