Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is

Given: Two poles of heights 6m and 11m stand vertically upright on a plane ground. Distance between their foot is 12 m.

To find: Distance between their tops.

Let CD be the pole with height 6m.

AB is the pole with height 11m, distance between their foot i.e. DB is 12 m.

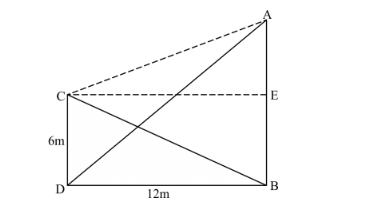
Let us assume a point E on the pole AB which is 6m from the base of AB.

Hence

AE = AB − 6 = 11 − 6 = 5 m

Now in right triangle AEC, Applying Pythagoras theorem

$\mathrm{AC}^{2}=\mathrm{AE}^{2}+\mathrm{EC}^{2}$

$\mathrm{AC}^{2}=5^{2}+12^{2}$ (since CDEB forms a rectangle and opposite sides of rectangle are equal)

$\mathrm{AC}^{2}=25+144$

$\mathrm{AC}^{2}=169$

$\mathrm{AC}=13 \mathrm{~m}$

Thus, the distance between their tops is 13m.

Hence correct answer is $(c)$.