Question:
Two tangents PQ and PR are drawn from an external point to a circle with centre 0. Prove that QORP is a cyclic quadrilateral.
Solution:
Given Two tangents PQ and PR are drawn from an external point to a circle with centre 0.
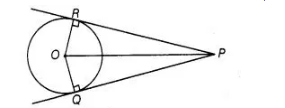
To prove QORP is a cyclic quadrilateral. proof Since, $P R$ and $P Q$ are tangents.
So, $O R \perp P R$ and $O Q \perp P Q$
[since, if we drawn a line from centre of a circle to its tangent line. Then, the line always perpendicular to the tangent line]
$\therefore$ $\angle O R P=\angle O Q P=90^{\circ}$
Hence. $\angle O R P+\angle O Q P=180^{\circ}$
So, $Q O P R$ is cyclic quadrilateral.
[If sum of opposite angles is quadriateral in $180^{\circ}$, then the quadrilateral is cyclic]
Hence proved.