Using Euler's formula find the unknown:

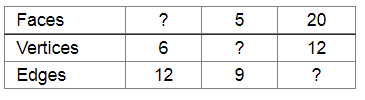
We know that the Euler's formula is: $\mathrm{F}+\mathrm{V}=\mathrm{E}+2$

(i)

The number of vertices $\mathrm{V}$ is 6 and the number of edges $\mathrm{E}$ is 12 .

Using Euler's formula:

$\mathrm{F}+6=12+2$

$\mathrm{~F}+6=14$

$\mathrm{~F}=14-6$

$\mathrm{~F}=8$

So, the number of faces in this polyhedron is 8 .

(ii)

Faces, $F=5$

Edges, $\mathrm{E}=9$.

We have to find the number of vertices.

Putting these values in Euler's formula:

$5+\mathrm{V}=9+2$

$5+\mathrm{V}=11$

$\mathrm{~V}=11-5$

$\mathrm{~V}=6$

So, the number of vertices in this polyhedron is 6 .

(iii)

Number of faces $F=20$

Number of vertices $\mathrm{V}=12$

Using Euler's formula:

$20+12=\mathrm{E}+2$

$32=\mathrm{E}+2$

$\mathrm{E}+2=32$

$\mathrm{E}=32-2$

$\mathrm{E}=30$

So, the number of edges in this polyhedron is 30 .