Using prime factorisation,

(a) Prime factors of $484=(2 \times 2) \times(11 \times 11)$

As grouping, there is no unpaired factor left over.

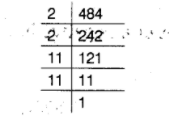
So, 484 is a perfect square.

(b) 11250

First we have to find out the factors by using prime factorisation method.

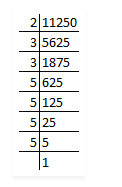
So, prime factors of 11250 = 2 × 3 × 3 × 5 × 5 × 5 × 5

Now, grouping the prime factors = 2 × (3 × 3) × (5 × 5) × (5 × 5)

= 2 × 32 × 52 × 52

Factor 2 has no pair.

∴11250 is not a perfect square.

(c) 841

First we have to find out the factors by using prime factorisation method.

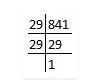
So, prime factors of 841 = 29 × 29

Now, grouping the prime factors = (29 × 29)

= 292

There is no unpaired factor remains here.

∴841 is a perfect square.

(d) 729

First we have to find out the factors by using prime factorisation method.

So, prime factors of 729 = 3 × 3 × 3 × 3 × 3 × 3

Now, grouping the prime factors = (3 × 3) × (3 × 3) × (3 × 3)

= 32 × 32 × 32

There is no unpaired factor remains here.

∴729 is a perfect square.