Using Pythagoras theorem determine the length of AD in terms of b and c shown in the given figure.

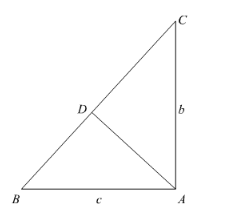
In $\triangle A B C$ and $\triangle D B A$,

$\angle A=\angle D \quad\left(90^{\circ}\right.$ each $)$

$\angle B=\angle B \quad$ (Common)

Therefore, by AA-criterion for similarity, we have $\triangle A B C \sim \triangle D B A$.

$\therefore \frac{A B}{B D}=\frac{B C}{B A}=\frac{A C}{A D}$

Now we will substitute the values of AC and AB

$\therefore \frac{c}{B D}=\frac{B C}{c}=\frac{b}{A D}$

We are finding the value of AD therefore; we will use the following ratios,

$\frac{B C}{c}=\frac{b}{A D}$

Now we will multiple both sides of the equation by $\frac{1}{b}$.

$\frac{B C}{c} \times \frac{1}{b}=\frac{b}{A D} \times \frac{1}{b}$

We will simplify the above equation as below,

$A D=\frac{b c}{B C}$...(1)

But we know that $B C=\sqrt{b^{2}+c^{2}}$ substituting the value of $\mathrm{BC}$ in equation (1) we get,

$A D=\frac{b c}{\sqrt{b^{2}+c^{2}}}$