Question:
Using the method of integration find the area bounded by the curve $|x|+|y|=1$
[Hint: the required region is bounded by lines $x+y=1, x-y=1,-x+y=1$ and $-x-y=11$ ]
Solution:
The area bounded by the curve, $|x|+|y|=1$, is represented by the shaded region ADCB as
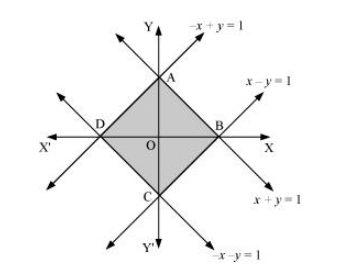
The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0).
It can be observed that the given curve is symmetrical about x-axis and y-axis.
∴ Area ADCB = 4 × Area OBAO
$=4 \int_{0}^{1}(1-x) d x$
$=4\left(x-\frac{x^{2}}{2}\right)_{0}^{1}$
$=4\left[1-\frac{1}{2}\right]$
$=4\left(\frac{1}{2}\right)$
$=2$ units
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
