Using the standard electrode potentials given in the Table 8.1, predict if the reaction between the following is feasible:
(a) $\mathrm{Fe}^{3+}(\mathrm{aq})$ and $\mathrm{I}^{-}(\mathrm{aq})$
(b) $\mathrm{Ag}^{+}(\mathrm{aq})$ and $\mathrm{Cu}(\mathrm{s})$
(c) $\mathrm{Fe}^{3+}$ (aq) and $\mathrm{Cu}$ (s)
(d) $\mathrm{Ag}(\mathrm{s})$ and $\mathrm{Fe}^{3+}(\mathrm{aq})$
(e) $\mathrm{Br}_{2}$ (aq) and $\mathrm{Fe}^{2+}$ (aq)
(a) The possible reaction between $\mathrm{Fe}_{(a q)}^{3+}+\mathrm{I}_{(a q)}^{-}$is given by,
$2 \mathrm{Fe}_{(\text {aq })}^{3+}+2 \mathrm{I}_{(\text {aq })}^{-} \longrightarrow 2 \mathrm{Fe}_{(\text {aq })}^{2+}+\mathrm{I}_{2(s)}$

$\mathrm{E}^{\circ}$ for the overall reaction is positive. Thus, the reaction between $\mathrm{Fe}_{(a q)}^{3+}$ and $\mathrm{I}_{(a q)}^{-}$is feasible.
(b) The possible reaction between $\mathrm{Ag}_{(a q)}^{+}+\mathrm{Cu}_{(s)}$ is given by,
$2 \mathrm{Ag}_{(a q)}^{+}+\mathrm{Cu}_{(s)} \longrightarrow 2 \mathrm{Ag}_{(s)}+\mathrm{Cu}_{(a q)}^{2+}$
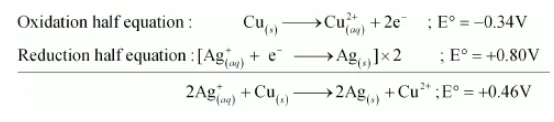
$\mathrm{E}^{\circ}$ positive for the overall reaction is positive. Hence, the reaction between $\mathrm{Ag}_{(a q)}^{+}$and $\mathrm{Cu}_{(x)}$ is feasible.
(d) The possible reaction between $\mathrm{Ag}_{(s)}$ and $\mathrm{Fe}_{(a q)}^{3+}$ is given by,
$\mathrm{Ag}_{(s)}+2 \mathrm{Fe}_{(a q)}^{3+} \longrightarrow \mathrm{Ag}_{(a q)}^{+}+\mathrm{Fe}_{(a q)}^{2+}$

Here, $\mathrm{E}^{\circ}$ for the overall reaction is negative. Hence, the reaction between $\mathrm{Ag}_{(s)}$ and $\mathrm{Fe}_{(a q)}^{3+}$ is not feasible
(e) The possible reaction between $\mathrm{Br}_{2(a q)}$ and $\mathrm{Fe}_{(a q)}^{2+}$ is given by,

Here, $\mathrm{E}^{\circ}$ for the overall reaction is positive. Hence, the reaction between $\mathrm{Br}_{2(a q)}$ and $\mathrm{Fe}_{(a q)}^{2+}$ is feasible.
