Question.
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Solution:
In $\triangle \mathrm{ABC}, \mathrm{D}$ is mid point of $\mathrm{AB}$ (see figure)
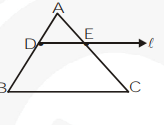
i.e., $\frac{A D}{D B}=1$
Straight line $\ell \| \mathrm{BC}$.
Line $\ell$ is drawn through $\mathrm{D}$ and it meets $\mathrm{AC}$ at $\mathrm{E}$.
By Basic Proportionality Theorem
$\frac{A D}{D B}=\frac{A E}{E C} \Rightarrow \frac{A E}{E C}=1[F r o m(1)]$
$\Rightarrow \mathrm{AE}=\mathrm{EC} \Rightarrow \mathrm{E}$ is mid point of $\mathrm{AC}$.
In $\triangle \mathrm{ABC}, \mathrm{D}$ is mid point of $\mathrm{AB}$ (see figure)

i.e., $\frac{A D}{D B}=1$
Straight line $\ell \| \mathrm{BC}$.
Line $\ell$ is drawn through $\mathrm{D}$ and it meets $\mathrm{AC}$ at $\mathrm{E}$.
By Basic Proportionality Theorem
$\frac{A D}{D B}=\frac{A E}{E C} \Rightarrow \frac{A E}{E C}=1[F r o m(1)]$
$\Rightarrow \mathrm{AE}=\mathrm{EC} \Rightarrow \mathrm{E}$ is mid point of $\mathrm{AC}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
