Verify the Gauss’s law for magnetic field

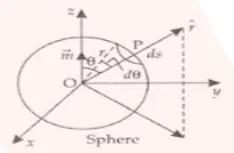
P is the point at a distance r from O and OP, then the magnetic field is given as:

$B=\frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{r^{3}} \hat{r}$

dS is the elementary area of the surface P, then

dS = r2 (r2 sin θ d θr)

$\oint B . d S=\oint \frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{r^{3}} \hat{r}\left(r^{2} \sin \theta d \theta \hat{r}\right)$

Solving the above we get,

$\oint B \cdot d S=-\frac{\mu_{0}}{4 \pi} \frac{M}{2 r}[1-1]=0$