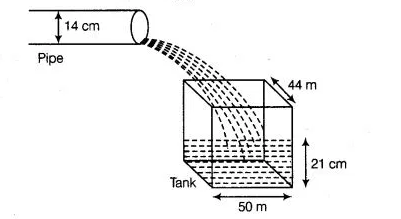
Water is flowing at the rate of 15 kmh-1 through

Given, length of the pond= 50 m and width of the pond = 44 m

Depth required of water $=21 \mathrm{~cm}=\frac{21}{100} \mathrm{~m}$

$\therefore \quad$ Volume of water in the pond $=\left(50 \times 44 \times \frac{21}{100}\right)^{3}=462 \mathrm{~m}^{3}$

Also, given radius of the pipe $=7 \mathrm{~cm}=\frac{7}{100} \mathrm{~m}$

and speed of water flowing through the pipe $=(15 \times 1000)=15000 \mathrm{mh}^{-1}$ Now, volume of water flow in $1 \mathrm{~h}=\pi R^{2} \mathrm{H}$

$=\left(\frac{22}{7} \times \frac{7}{100} \times \frac{7}{100} \times 15000\right)$

$=231 \mathrm{~m}^{3}$

Since, $231 \mathrm{~m}^{3}$ of water falls in the pond in $1 \mathrm{~h}$.

So, $1 \mathrm{~m}^{3}$ water falls in the pond in $\frac{1}{231} \mathrm{~h}$.

Also, $462 \mathrm{~m}^{3}$ of water falls in the pond in $\left(\frac{1}{231} \times 462\right) \mathrm{h}=2 \mathrm{~h}$

Hence, the required time is 2 h.