Question:
Weekly income of 600 families is tabulated below
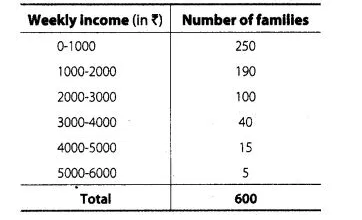
Compute the median income.
Solution:
First we construct a cumulative frequency table
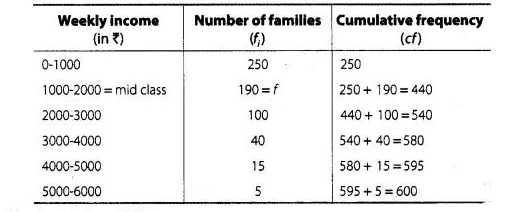
It is given that, $n=600$
$\therefore$ $\frac{n}{2}=\frac{600}{2}=300$
Since, cumulative frequency 440 lies in the interval $1000-2000$.
Here, (lower median class) $l=1000$,
$f=190, c f=250$, (class width) $h=1000$
and (total observation) $n=600$
$\therefore$ Median $=l+\frac{\left\{\frac{n}{2}-c f\right\}}{f} \times n$
$=1000+\frac{(300-250)}{190} \times 1000$
$=1000+\frac{50}{190} \times 1000$
$=1000+\frac{5000}{19}$
$=1000+263.15=1263.15$
Hence, the median income is ₹ 1263.15.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
