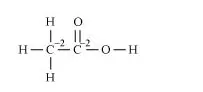What are the oxidation numbers of the underlined elements in each of the following and how do you rationalise your results?

(a) KI3

In $\mathrm{KI}_{3}$, the oxidation number ( $\mathrm{O} . \mathrm{N}$.) of $\mathrm{K}$ is $+1$. Hence, the average oxidation number of $\mathrm{I}$ is $-\frac{1}{3}$. However, $\mathrm{O} . \mathrm{N}$. cannot be fractional. Therefore, we will have to consider the structure of $\mathrm{Kl}_{3}$ to find the oxidation states.

In a $\mathrm{Kl}_{3}$ molecule, an atom of iodine forms a coordinate covalent bond with an iodine molecule.

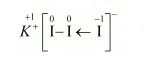
Hence, in a KI3molecule, the O.N. of the two I atoms forming the I2molecule is 0, whereas the O.N. of the I atom forming the coordinate bond is –1.

(b) $\mathrm{H}_{2} \mathrm{~S}_{4} \mathrm{O}_{6}$

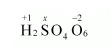
Now, $2(+1)+4(x)+6(-2)=0$

$\Rightarrow 2+4 x-12=0$

$\Rightarrow 4 x=10$

$\Rightarrow x=+2 \frac{1}{2}$

However, O.N. cannot be fractional. Hence, S must be present in different oxidation states in the molecule.

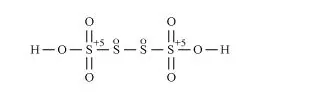
The O.N. of two of the four $S$ atoms is $+5$ and the $O . N$. of the other two $S$ atoms is 0 .

(c) $\mathrm{Fe}_{3} \mathrm{O}_{4}$

On taking the O.N. of $\mathrm{O}$ as $-2$, the O.N. of Fe is found to be $+2 \frac{2}{3}$. However, O.N. cannot be fractional.

Here, one of the three Fe atoms exhibits the O.N. of $+2$ and the other two Fe atoms exhibit the O.N. of $+3$.

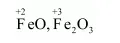
(d) $\mathrm{CH}_{3} \underline{\mathrm{CH}}_{2} \mathrm{OH}$

$2(x)+6(+1)+1(-2)=0$

or, $2 x+4=0$

or, $x=-2$

Hence, the $O \cdot N$. of $C$ is $-2$.

(e) $\underline{\mathrm{CH}}_{3} \underline{\mathrm{COOH}}$

$2(x)+4(+1)+2(-2)=0$

or, $2 x=0$

or, $x=0$

However, 0 is average O.N. of C. The two carbon atoms present in this molecule are present in different environments. Hence, they cannot have the same oxidation number. Thus, $\mathrm{C}$ exhibits the oxidation states of $+2$ and $-2$ in $\mathrm{CH}_{3} \mathrm{COOH}$.