What is an adsorption isotherm?

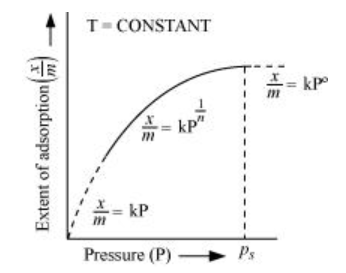
The plot between the extent of adsorption $\left(\frac{x}{m}\right)$ against the pressure of gas $(P)$ at constant temperature $(T)$ is called the adsorption isotherm.

Freundlich adsorption isotherm:

Freundlich adsorption isotherm gives an empirical relationship between the quantity of gas adsorbed by the unit mass of solid adsorbent and pressure at a specific temperature.

From the given plot it is clear that at pressure $P_{S}, \frac{x}{m}$ reaches the maximum valve. $P_{S}$ is called the saturation pressure.

Three cases arise from the graph now.

Case I- At low pressure:

The plot is straight and sloping, indicating that the pressure in directly proportional to $\frac{x}{m}$ i.e., $\frac{x}{m} \alpha P$.

$\frac{x}{m}=k P$      ( $k$ is a constant)

Case II- At high pressure:

When pressure exceeds the saturated pressure, $\frac{x}{m}$ becomes independent of $P$ values.

$\frac{x}{m} \alpha P^{\circ}$

$\frac{x}{m}=k P^{\circ}$

Case III- At intermediate pressure:

At intermediate pressure, $\frac{x}{m}$ depends on $P$ raised to the powers between 0 and $1 .$ This relationship is known as the Freundlich adsorption isotherm.

$\frac{x}{m} \alpha P^{\frac{1}{n}}$

$\frac{x}{m}=k P^{\frac{1}{n}} \quad n>1$

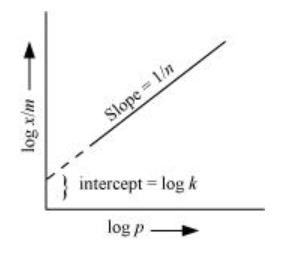
Now, taking log:

$\log \frac{x}{m}=\log k+\frac{1}{n} \log P$

On plotting the graph between $\log \left(\frac{x}{m}\right)$ and $\log P$, a straight line is obtained with the slope equal to $\frac{1}{n}$ and the intercept equal to log $\mathrm{k}$.