What type of quadrilateral do the points A (2, -2),

To find the type of quadrilateral, we find the length of all four sides as well as two diagonals and see whatever condition of quadrilateral is satisfy by

these sides as well as diagonals. Now, using distance formula between two points,

sides, $A B=\sqrt{(7-2)^{2}+(3+2)^{2}}$

$=\sqrt{(5)^{2}+(5)^{2}}=\sqrt{25+25}$

$=\sqrt{50}=5 \sqrt{2}$

$\left[\right.$ since, distance between two points $\left(x_{1}, y_{1}\right)$ and $\left.\left(x_{2}, y_{2}\right)=\sqrt{\left(x_{2}-x_{1}\right)+\left(y_{2}-y_{1}\right)^{2}}\right]$

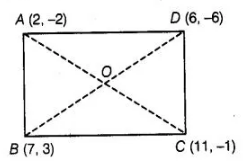
$B C=\sqrt{(11-7)^{2}+(-1-3)^{2}}=\sqrt{(4)^{2}+(-4)^{2}}$

$C D=\sqrt{(6-11)^{2}+(-6+1)^{2}}$

$=\sqrt{(-5)^{2}+(-5)^{2}}$

$=\sqrt{25+25}=\sqrt{50}=5 \sqrt{2}$

and $D A=\sqrt{(2-6)^{2}+(-2+6)^{2}}$

$=\sqrt{(-4)^{2}+(4)^{2}}=\sqrt{16+16}$

$=\sqrt{32}=4 \sqrt{2}$

Diagonals, $A C=\sqrt{(11-2)^{2}+(-1+2)^{2}}$

$=\sqrt{(9)^{2}+(1)^{2}}=\sqrt{81+1}=\sqrt{82}$

and $B D=\sqrt{(6-7)^{2}+(-6-3)^{2}}$

$=\sqrt{(-1)^{2}+(-9)^{2}}$

$=\sqrt{1+81}=\sqrt{82}$

Here, we see that the sides AB = CD and BC = DA

Also, diagonals are equal i.e., AC = BD

which shows the quadrilateral is a rectangle.