When a car is at rest, its driver sees rain drops falling on it vertically. When driving the car with speed $\mathrm{v}$, he sees that rain drops are coming at an angle $60^{\circ}$ from the horizontal. On further increasing the speed of the car to $(1+\beta) \mathrm{v}$, this angle changes to $45^{\circ}$. The value of $\beta$ is close to:
Correct Option: , 4
Rain is falling vertically downwards.
$\overrightarrow{\mathrm{V}}_{\mathrm{r} / \mathrm{m}}=\overrightarrow{\mathrm{V}}_{\mathrm{r}}-\overrightarrow{\mathrm{v}}_{\mathrm{m}}$
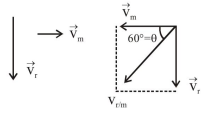
$\tan 60^{\circ}=\frac{v_{r}}{v_{m}}=\sqrt{3}$
$v_{r}=v_{m} \sqrt{3}=v \sqrt{3}$
Now, $v_{m}=(1+B) v$
and $\theta=45^{\circ}$
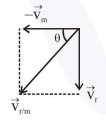
$\tan 45=\frac{v_{r}}{v_{m}}=1$
$\mathrm{V}_{\mathrm{r}}=\mathrm{V}_{\mathrm{m}}$
$\mathrm{v} \sqrt{3}=(1+\beta) \mathrm{v}$
$\sqrt{3}=1+\beta$
$\Rightarrow \beta=\sqrt{3}-1=0.73$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
