When a car si at rest, its driver sees raindrops falling on it vertically. When driving the car with speed $v$, he sees that raindrops are coming at an angle $60^{\circ}$ from the horizontal. On furter increasing the speed of the car to $(1+\beta) v$, this angle changes to $45^{\circ}$. The value of $\beta$ is close to:
Correct Option: , 4
(4) The given situation is shown in the diagram. Here $v_{r}$ be the velocity of rain drop.
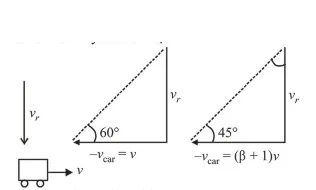
When car is moving with speed $v$,
$\tan 60^{\circ}=\frac{v_{r}}{v}$ ...(i)
When car is moving with speed $(1+\beta) v$,
$\tan 45^{\circ}=\frac{v_{r}}{(\beta+1) v}$ ....(ii)
Dividing (i) by (ii) we get,
$\sqrt{3} v=(\beta+1) v \Rightarrow \beta=\sqrt{3}-1=0.732$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.