Question:
When a particle of mass $m$ is attached to a vertical spring of spring constant $\mathrm{k}$ and released, its motion is described by $y(t)=y_{0} \sin ^{2} \omega t$, where ' $y$ ' is measured from the lower end of unstretched spring. Then $\omega$ is :
Correct Option: , 2
Solution:
$\mathrm{y}=\mathrm{y}_{0} \sin ^{2} \omega \mathrm{t}$
$y=\frac{y_{0}}{2}(1-\cos 2 \omega t)$
$y-\frac{y_{0}}{2}=-\frac{y_{0}}{2} \cos 2 \omega t$
Amplitude : $\frac{\mathrm{y}_{0}}{2}$
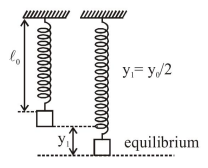
$\frac{y_{0}}{2}=\frac{m g}{K}$
$2 \omega=\sqrt{\frac{K}{m}}=\sqrt{\frac{2 g}{y_{0}}}$
$\omega=\sqrt{\frac{g}{2 y_{0}}}$
Ans.(2)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.