Write the number of ways in which 7 men and 7 women can sit on a round table such that no two women sit together.
Question:
Write the number of ways in which 7 men and 7 women can sit on a round table such that no two women sit together.
Solution:
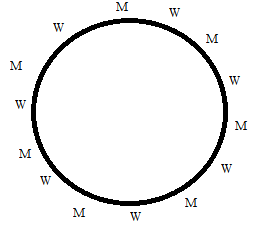
Each of the seven men can be arranged amongst themselves in 7! ways.
The women can be arranged amongst themselves in seven places, in 6! ways (i.e. n things can be arranged in (n-1)! ways around a round table).
By fundamental principle of counting, total number of ways $=7 ! \times 6 !$