XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and E respectively

Solution:



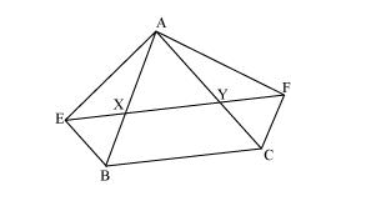
It is given that

$X Y\|B C \Rightarrow E Y\| B C$

$B E\|A C \Rightarrow B E\| C Y$

Therefore, $\mathrm{EBCY}$ is a parallelogram.

It is given that

$X Y\|B C \Rightarrow X F\| B C$

$\mathrm{FC}\|\mathrm{AB} \Rightarrow \mathrm{FC}\| \mathrm{XB}$

Therefore, BCFX is a parallelogram.

Parallelograms EBCY and BCFX are on the same base BC and between the same parallels BC and EF.

$\therefore$ Area $(\mathrm{EBCY})=$ Area $(\mathrm{BCFX}) \ldots(1)$

Consider parallelogram EBCY and $\triangle A E B$

These lie on the same base $B E$ and are between the same parallels $B E$ and $A C$.

$\therefore$ Area $(\triangle \mathrm{ABE})=\frac{1}{2}$ Area $(\mathrm{EBCY})$..(2)

Also, parallelogram $B C F X$ and $\triangle A C F$ are on the same base $C F$ and between the same parallels $C F$ and $A B$.

$\therefore$ Area $(\triangle \mathrm{ACF})=\frac{1}{2}$ Area $(\mathrm{BCFX}) \ldots$(3)

From equations $(1),(2)$, and $(3)$, we obtain

Area $(\triangle \mathrm{ABE})=$ Area $(\triangle \mathrm{ACF})$