XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =

Given: XY is drawn parallel to the base BC of a ΔABC cutting AB at X and AC at Y. AB = 4BX and YC = 2 cm.

To find: AY

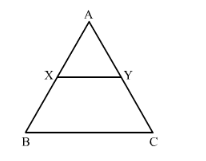
In ΔAXY and ΔABC,

∠AXY=∠B                   Corresponding angles∠A=∠A                        Common∴∆AXY~∆ABC          AA similarity
 

We know that if two triangles are similar, then their sides are proportional.

It is given that AB = 4BX.

Let AB = 4x and BX = x.

Then, AX = 3x

$\frac{\mathrm{AX}}{\mathrm{BX}}=\frac{\mathrm{AY}}{\mathrm{YC}}$

$\frac{3 x}{1 x}=\frac{\mathrm{AY}}{2}$

$\mathrm{AY}=\frac{3 x \times 2}{1 x}$

$\mathrm{AY}=6 \mathrm{~cm}$

Hence the correct answer is C