RD Sharma Solutions for Class 9 Maths Chapter 16 Circles

Hey, are you a class 9 student and looking for ways to download RD Sharma Solutions for Class 9 Maths Chapter 16 "Circles "? If yes. Then read this post till the end.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 16 in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to learn and understand class 9 Maths Chapter 16 "Circles " in an easy way then you can use these solutions PDF.

Chapter 16 of RD Sharma Class 9 deals with Circles , their different types and formulas. If you want to improve your basic in Circles , then you can use this.

RD Sharma Solutions helps students to Practice important concepts of subjects easily. RD Sharma class 9 solutions provide detailed explanations of all the  exercise questions that students can use to clear their doubts instantly.

If you want to become good at Math then it is very important for you to have a good knowledge of all the important topics of class 9 math, so to learn and practice those topics you can use eSaral RD Sharma Solutions.

In this article, we have listed RD Sharma Solutions for Class 9 Maths Chapter 16 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

RD Sharma Solutions for Class 9 Maths Chapter 16 Circles - Free PDF Download

Question 1: In the given figure, $\triangle A B C$ is an equilateral triangle. Find $m \angle B E C$.



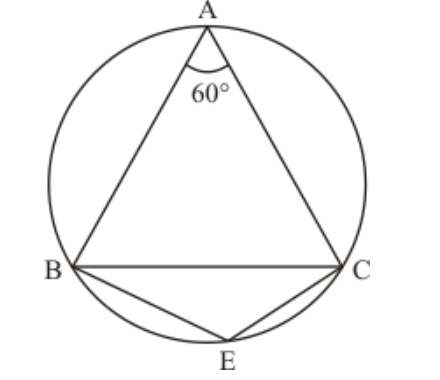
Solution. It is given that, $\triangle A B C$ is an equilateral triangle



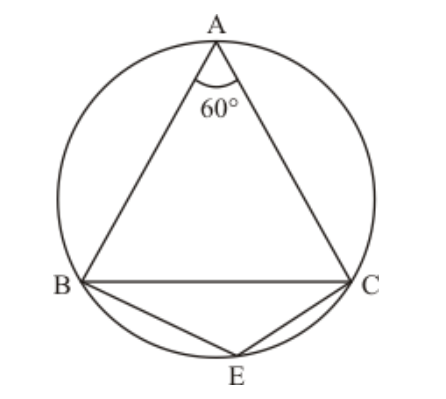
We have to find $\mathrm{m} \angle B E C$

Since $\triangle A B C$ is an equilateral triangle.

So $\angle A+\angle B+\angle C=180^{\circ}$

And

$\angle A=\angle B=\angle C=60^{\circ} \ldots$(1)

Since, quadrilateral $B A C E$ is a cyclic qualdrilateral

So, $\angle A+\angle E=180^{\circ}$(Sum of opposite angles of cyclic quadrilateral is $180^{\circ}$.)

$60^{\circ}+\angle E=180^{\circ}$

$\angle E=120^{\circ}$

Hence

$\mathrm{m} \angle B E C=120^{\circ}$

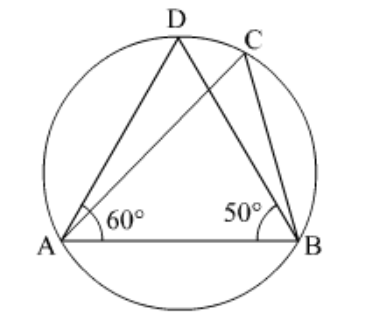
Question 2: In the given figure, $\triangle P Q R$ is an isosceles triangle with $P Q=P R$ and $m \angle P Q R=35^{\circ}$. Find $m \angle Q S R$ and $m \angle Q T R$.



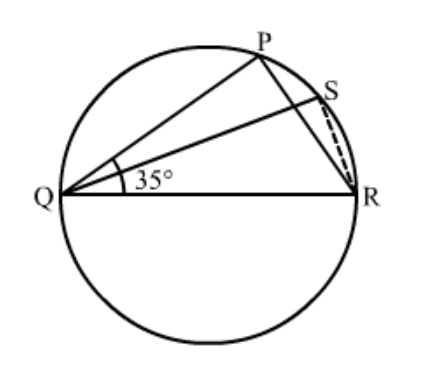
Solution. Disclaimer: Figure given in the book was showing $m \angle P Q R$ as $m \angle S Q R$.

It is given that $\Delta P Q R$ is an isosceles triangle with $P Q=P R$ and $m \angle P Q R=35^{\circ}$



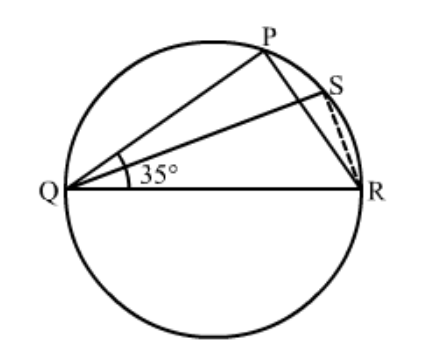
We have to find the $\mathrm{m} \angle Q S R$ and $\mathrm{m} \angle Q T R$

Since $\triangle P Q R$ is an isosceles triangle

So $\angle P Q R=\angle P R Q=35^{\circ}$

Then

$\angle Q P R=180^{\circ}-(\angle P Q R+\angle P R Q)$

$=180^{\circ}-\left(35^{\circ}+35^{\circ}\right)$

$=180^{\circ}-70^{\circ}$

$=110^{\circ}$

Since $P Q T R$ is a cyclic quadrilateral

So

$\angle P+\angle T=180^{\circ}$

$\angle T=180^{\circ}-110^{\circ}$

$=70^{\circ}$

In cyclic quadrilateral $Q S R T$ we have

$\angle S+\angle T=180^{\circ}$

$\angle S=180^{\circ}-70^{\circ}$

$=110^{\circ}$

Hence,

$\mathrm{m} \angle Q S R=110^{\circ}$ and $\angle Q T R=70^{\circ}$

Question 3: In the given figure, $O$ is the centre of the circle. If $\angle B O D=160^{\circ}$, find the values of $x$ and $y$.



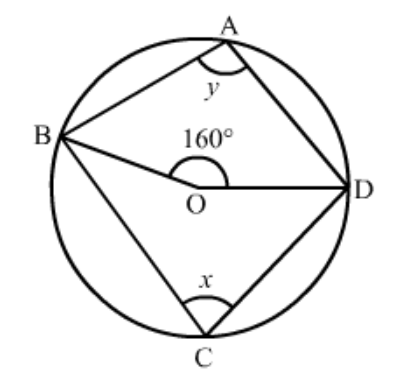
Solution. It is given that $O$ is centre of the circle and $\angle B O D=160^{\circ}$



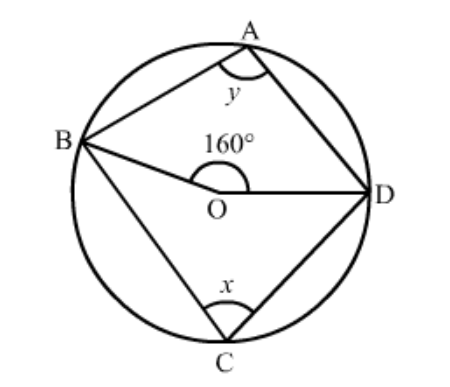
We have to find the values of $x$ and $y .$

As we know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

Therefore,

$x=\frac{1}{2}\left(160^{0}\right)$

$=80^{\circ}$

Since, quadrilateral $A B C D$ is a cyclic quadrilateral.

So,

$x+y=180^{\circ}$

(Sum of opposite angles of a cyclic quadrilateral is $180^{\circ}$.)

$y=180^{\circ}-x$

$=180^{\circ}-80^{\circ}$

$=100^{\circ}$

Hence $\angle y=100^{\circ}$ and $\angle x=80^{\circ}$

Question 4: In the given figure, $A B C D$ is a cyclic quadrilateral. If $\angle B C D=100^{\circ}$ and $\angle A B D=70^{\circ}$, find $\angle A D B$.



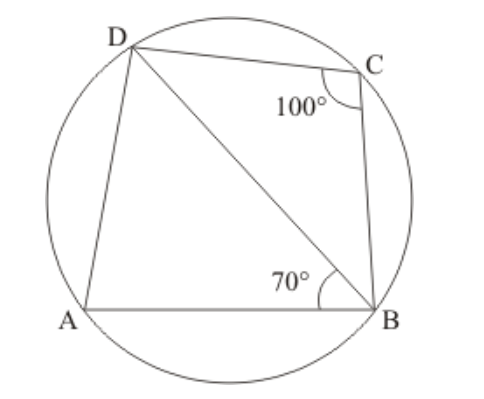
Solution. It is given that $\angle B C D=100^{\circ}$ and $\angle A B D=70^{\circ}$



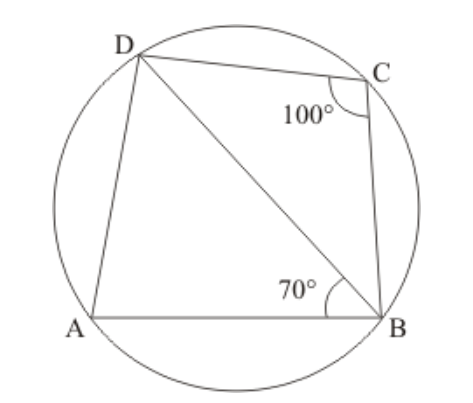
We have to find the $\angle A D B$

We have

$\angle A+\angle C=180^{\circ}$

(Opposite pair of angle of cyclic quadrilateral)

So,

$\angle A=180^{\circ}-100^{\circ}$

$=80^{\circ}$

Now in $\triangle A D B$ is $\angle A=80^{\circ}$ and $\angle A B D=70^{\circ}$

Therefore,

$\angle A+\angle A D B+\angle A B D=180^{\circ}$

$80^{\circ}+\angle A D B+70^{\circ}=180^{\circ}$b

$\angle A D B=180^{\circ}-150^{\circ}$

$=30^{\circ}$

Hence, $\angle A D B=30^{\circ}$

Question 5: If $A B C D$ is a cyclic quadrilateral in which $A D \| B C$ (In the given figure). Prove that $\angle B=\angle C$.



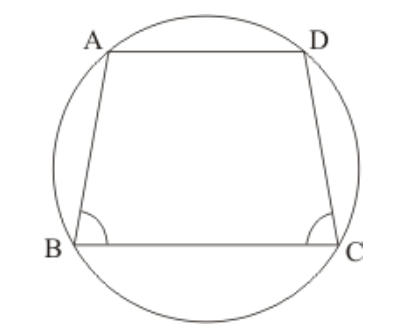
Solution. It is given that, $A B C D$ is cyclic quadrilateral in which $A D \| B C$



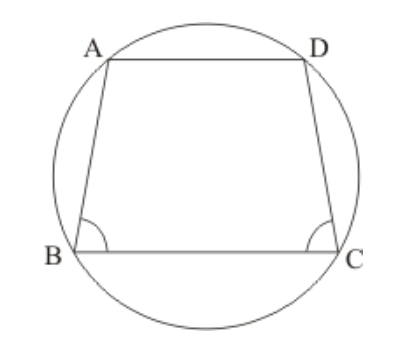
We have to prove $\angle B=\angle C$

Since, $A B C D$ is a cyclic quadrilateral

So,

$\angle B+\angle D=180^{\circ}$ and $\angle A+\angle C=180^{\circ} \cdots$(1)

$\Rightarrow \angle B+\angle A=180^{\circ}$ and $\angle C+\angle D=180^{\circ}$

(Sum of pair of consecutive interior angles is $\left.180^{\circ}\right) \ldots \ldots$(2)

From equation (1) and (2) we have

$\angle B+\angle D+\angle B+\angle A=360^{\circ} \ldots$(3)

$\angle A+\angle C+\angle C+\angle D=360^{\circ} \ldots$(3)

$\angle A+\angle C+\angle C+\angle D=360^{\circ} \ldots$(4)

$2 \angle B+\angle D+\angle A=2 \angle C+\angle A+\angle D$

$2 \angle B=2 \angle C$

$\angle B=\angle C$

Hence Proved

Question 6: In the given figure, $O$ is the centre of the circle. Find $\angle C B D$.



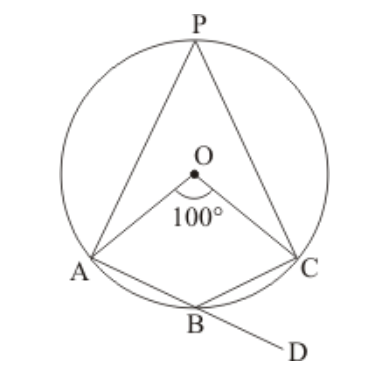
Solution. It is given that, $\angle A O C=100^{\circ}$



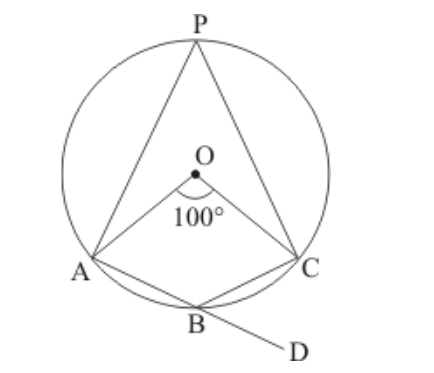
We have to find $\angle C B D$

Since, $\angle A O C=100^{\circ}$ (Given)

So,

$\angle A P C=\frac{1}{2} \angle A O C$

(The angle subtended by an arc of a circle at the centre is double theangle subtended by it at any point on the remaining part of the circle.)

$\Rightarrow \angle A P C=\frac{1}{2} \times 100$

$=50^{\circ}$

Now,

$\angle A P C+\angle A B C=180^{\circ}$

(Opposite pair of angle of cyclic quadrilateral)

So,

$50^{\circ}+\angle A B C=180^{\circ}$

$\angle A B C=180^{\circ}-50^{\circ}$

$=130^{\circ}$

$\Rightarrow \angle A B C=130^{\circ} \ldots \ldots$(1)

$\angle A B C+\angle C B D=180^{\circ}$ (Linear pair)

$130^{\circ}+\angle C B D=180^{\circ} \quad\left(\angle A B C=130^{\circ}\right)$

$\angle C B D=180^{\circ}-130^{\circ}$

$=50^{\circ}$

Hence $\angle C B D=50^{\circ}$

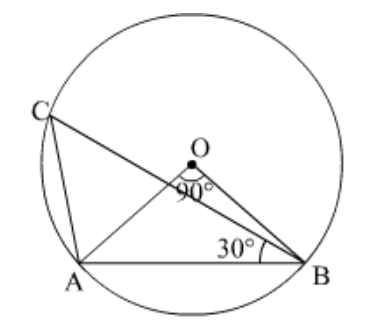
Question 7: In the given figure, $A B$ and $C D$ are diameters of a circle with centre $O$. If $\angle O B D=50^{\circ}$, find $\angle A O C$.



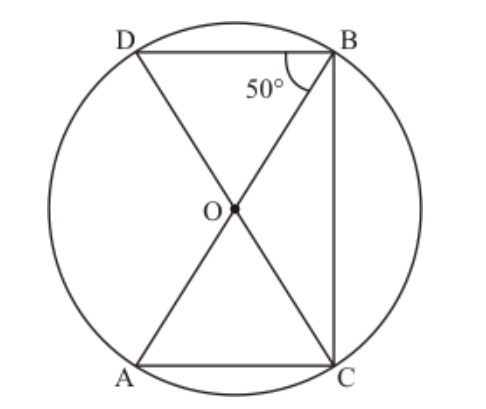
Solution. It is given that, $A B$ and $C D$ are diameter with center $O$ and $\angle O B D=50^{\circ}$



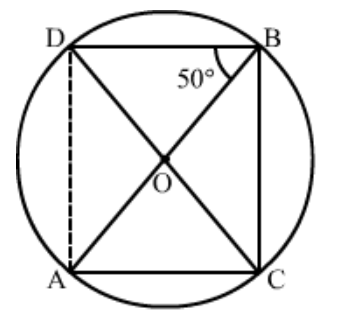
We have to find $\angle A O C$

Construction: Join the point $A$ and $D$ to form line $A D$

Clearly arc $A D$ subtends $\angle A B D=50^{\circ}$ at $B$ and $\angle A O D$ at the centre

Therefore, $\angle A O D=2 \angle A B D=100^{\circ} \ldots \ldots$ (1)

Since $C D$ is a straight line then

$\angle D O A+\angle A O C=180^{\circ}$ (Linear pair)

$\angle A O C=180^{\circ}-100^{\circ}$

$=80^{\circ}$

Hence $\angle A O C=80^{\circ}$

Question 8: On a semi-circle with $A B$ as diameter, a point $C$ is taken, so that $m(\angle C A B)=30^{\circ}$. Find $m(\angle A C B)$ and $\mathrm{m}(\angle A B C)$.

Solution. It is given that, $A B$ as diameter, $O$ is centre and $\angle C A B=30^{\circ}$



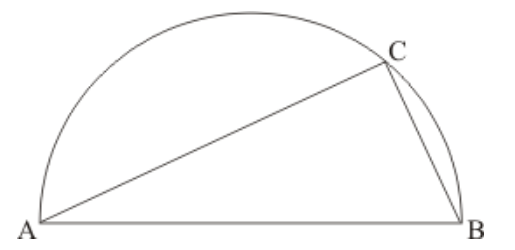
We have to find $\mathrm{m} \angle A C B$ and $\mathrm{m} \angle A B C$

Since angle in a semi-circle is a right angle therefore

$\angle A C B=90^{\circ}$

In $\triangle A C D$ we have

$\angle C A B=30^{\circ}$ (Given)

$\angle A C B=90^{\circ}$ (Angle in semi-circle is right angle)

Now in $\triangle A C B$ we have

$\angle C A B+\angle A C B+\angle A B C=180^{\circ}$

$\angle A B C=180^{\circ}-(\angle C A B+\angle C A B)$

$=180^{\circ}-\left(90^{\circ}+30^{\circ}\right)$

$=180^{\circ}-120^{\circ}$

$=60^{0}$

Hence $\angle A B C=60^{\circ}$ and $\angle A C B=90^{\circ}$

Question 9: In a cyclic quadrilateral $A B C D$ if $A B \| C D$ and $\angle B=70^{\circ}$, find the remaining angles.

Solution. It is given that, $A B C D$ is a cyclic quadrilateral such that $A B \| C D$ and $\angle B=70^{\circ}$



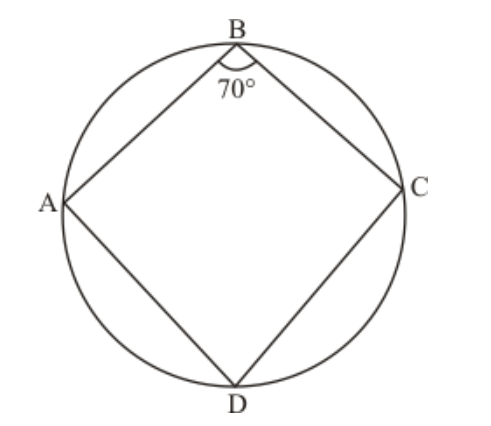
Sum of pair of opposite angles of cyclic quadrilateral is $180^{\circ}$.

$\angle B+\angle D=180^{\circ} \quad\left(\angle B=70^{\circ}\right.$ given $)$

So, $\angle D=110^{\circ}$

Also $A B \| C D$ and $B C$ transversal

So,

$\angle B+\angle C=180^{\circ}$

$\angle C=180^{\circ}-70^{\circ}$

$=110^{\circ}$

Now

$\angle A+\angle C=180^{\circ}$

$\angle A=180^{\circ}-\angle C$

$=180^{\circ}-110^{\circ}$

$=70^{\circ}$

$\angle D=180^{\circ}-70^{\circ}$

$\angle D=110^{\circ}$

Question 10: In a cyclic quadrilateral $A B C D$, if $m \angle A=3(m \angle C)$. Find $m \angle A$.

Solution. It is given that

$A B C D$ is cyclic quadrilateral and $\mathrm{m} \angle A=3(\mathrm{~m} \angle C)$



We have to find $\mathrm{m} \angle A$

Since $A B C D$ is cyclic quadrilateral and sum of opposite pair of cyclic quadrilateral is $180^{\circ}$.

So $\angle A+\angle C=180^{\circ}$

And

$3 \angle C+\angle C=180^{\circ}$

$4 \angle C=180^{\circ}$

$\angle C=\frac{180^{\circ}}{4}$

$=45^{\circ}$

Therefore

$\angle A=3 \times 45^{0}$

$=135^{\circ}$

Hence $\angle A=135^{\circ}$

Question 11: In the given figure, $O$ is the centre of the circle and $\angle D A B=50^{\circ}$. Calculate the values of $x$ and $y$.



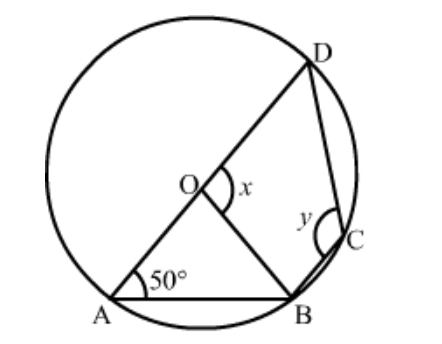
Solution. It is given that, $O$ is the centre of the circle and $\angle D A B=50^{\circ}$.



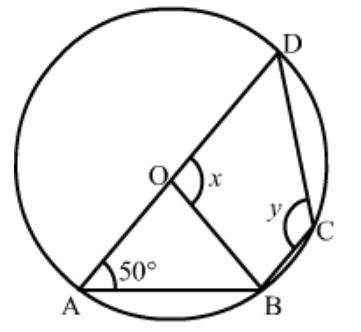
We have to find the values of $x$ and $y$.

$A B C D$ is a cyclic quadrilateral and $\angle A+\angle C=180^{\circ}$

So,

$50^{\circ}+y=180^{\circ}$

$y=180^{\circ}-50^{\circ}$

$y=130^{\circ}$

Clearly $\Delta O A B$ is an isosceles triangle with $O A=O B$ and $\angle O B A=\angle O A B$

Then, $\angle O B A+\angle O A B+\angle A O B=180^{\circ}$

$\angle A O B=180^{\circ}-\left(50^{\circ}+50^{\circ}\right)$

(Since $\left.\angle O B A=\angle O A B=50^{\circ}\right)$

So, $\angle A O B=80^{\circ}$

$x+\angle A O B=180^{\circ}$ (Linear pair)

Therefore, $x=180^{\circ}-80^{\circ}=100^{\circ}$

Hence,

$x=100^{\circ}$

And

$y=130^{\circ}$

Question 12: In the given figure, if $\angle B A C=60^{\circ}$ and $\angle B C A=20^{\circ}$, find $\angle A D C$.



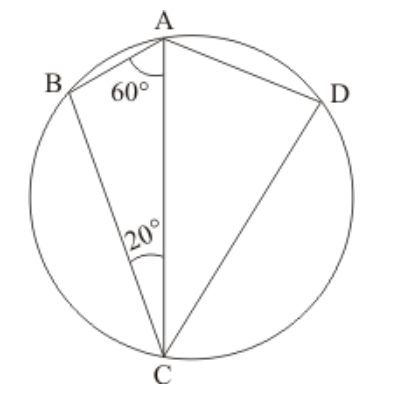
Solution. It is given that, $\angle B A C=60^{\circ}$ and $\angle B C A=20^{\circ}$



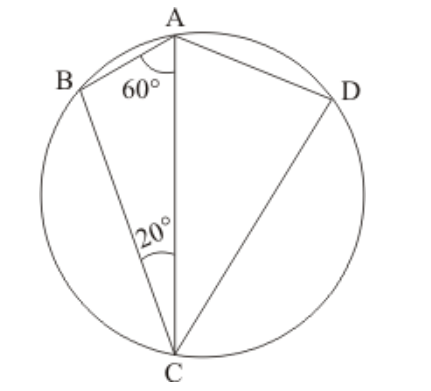
We have to find the $\angle A D C$

In given $\triangle A B C$ we have

$\angle A B C+\angle B C A+\angle B A C=180^{\circ}$ (Angle sum property)

$\Rightarrow \angle A B C=180^{\circ}-\left(60^{\circ}+20^{\circ}\right)=100^{\circ}$

In cyclic quadrilateral $A B C D$ we have

$\angle B+\angle D=180^{\circ}$

(Sum of pair of opposite angles of a cyclic quadilateral is $180^{\circ}$ )

Then,

$\angle D=180^{\circ}-100^{\circ}$

$\angle D=80^{\circ}$

Hence $\angle A D C=80^{\circ}$

Question 13: In the given figure, if $A B C$ is an equilateral triangle. Find $\angle B D C$ and $\angle B E C$.



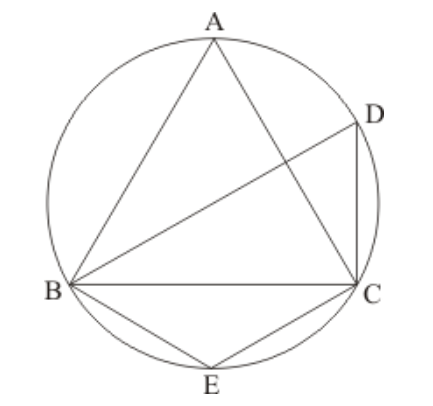
Solution. It is given that, $A B C$ is an equilateral triangle



We have to find $\angle B D C$ and $\angle B E C$

Since $\triangle A B C$ is an equilateral triangle

So, $\angle A=\angle B=\angle C=60^{\circ}$

And $A B E C$ is cyclic quadrilateral

So $\angle A+\angle E=180^{\circ}$

(Sum of opposite pair of angles of a cyclic quadrilateral is $180^{\circ}$.)

Then,

$\angle E=180^{\circ}-60^{\circ}$

$=120^{\circ}$

Similarly $B E C D$ is also cyclic quadrilateral

So,

$\angle E+\angle D=180^{\circ}$

$\angle D=180^{\circ}-120^{\circ}$

$=60^{\circ}$

Hence, $\angle B D C=60^{\circ}$ and $\angle B E C=120^{\circ}$.

Question 14: In the given figure, $O$ is the centre of the circle. If $\angle C E A=30^{\circ}$, Find the values of $x, y$ and $z$.



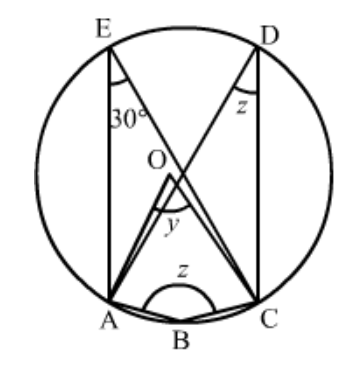
Solution. It is given that, $O$ is the centre of the circle and $\angle A E C=30^{\circ}$



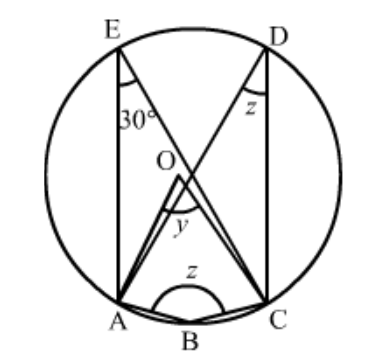
We have to find the value of $x, y$ and $z$.

Since, angle in the same segment are equal

So $\angle A E C=\angle A D C=30^{\circ}$

And $z=30^{\circ}$

As angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

Since $\angle A O C=2 \angle A D C$

Then,

$y=2 z$

$=2 \times 30^{\circ}$

$=60^{\circ}$

Since, the sum of opposite pair of angles of a cyclic quadrilateral is $180^{\circ}$.

$z+x=180^{\circ}$

$x=180^{\circ}-30^{\circ}$

$=150^{\circ}$

Hence,

$x=150^{\circ}, y=60^{\circ} \text { and } z=30^{\circ}$

Question 15: In the given figure, $\angle B A D=78^{\circ}, \angle D C F=x^{\circ}$ and $\angle D E F=y^{\circ} .$ Find the values of $x$ and $y$.



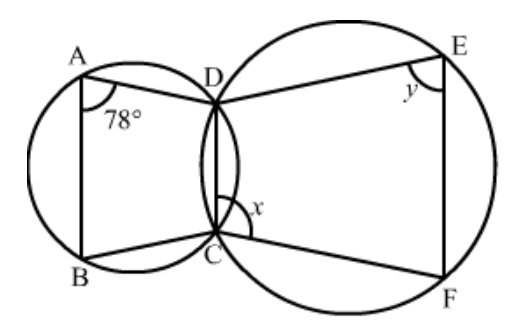
Solution. It is given that, $\angle A=78^{0}$ and $A B C D, D C F E$ are cyclic quadrilateral



We have to find the value of $x$ and $y$.

Since, $A B C D$ is a cyclic quadrilateral

So $\angle A+\angle B C D=180^{\circ}$

(Opposite angle of a cyclic quadrilateral are supplementary)

$\angle B C D=180^{\circ}-\angle A \quad\left(\angle A=78^{\circ}\right)$

$\angle B C D=180^{\circ}-78^{\circ}$

$\angle B C D=102^{\circ} \ldots \ldots$ (1)

$\angle B C D+\angle D C F=180^{\circ}$

$\angle D C F=180^{\circ}-\angle B C D$

$x=180^{\circ}-102^{\circ}$

$=78^{\circ}$

Now in cyclic quadrilateral $D C F E$

$x+y=180^{\circ} \quad$ (Opposite angles of a cyclic quadrilateral are supplementary)

$y=180^{\circ}-78^{\circ}$

$=102^{\circ}$

Hence, $x=78^{\circ}$ and $y=102^{\circ}$

Question 16: In a cyclic quadrilateral $A B C D$, if $\angle A-\angle C=60^{\circ}$, prove that the smaller of two is $60^{\circ}$

Solution. It is given that $\angle A-\angle C=60^{\circ}$ and $A B C D$ is a cyclic quadrilateral.



We have to prove that smaller of two is $60^{\circ}$

Since $A B C D$ is a cyclic quadrilateral

So $\angle A+\angle C=180^{\circ}$

(Sum of opposite pair of angles of cyclic quadrilateral is $180^{\circ}$ ) $\ldots \cdots$ (1)

And,

$\angle A-\angle C=60^{\circ}$ (Given) $\ldots .(2)$

Adding equation (1) and (2) we have

$2 \angle A=240^{\circ}$

$\angle A=\frac{240^{\circ}}{2}$

$=120^{\circ}$

So, $\angle C=60^{\circ}$

Hence, smaller of two is $60^{\circ}$.

Question 17: In the given figure, $A B C D$ is a cyclic quadrilateral. Find the value of $x$.



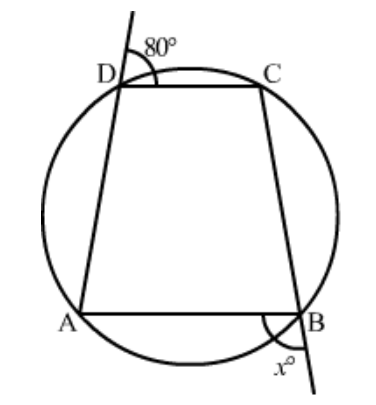
Solution. Here, $A B C D$ is a cyclic quadrilateral, we need to find $x$.



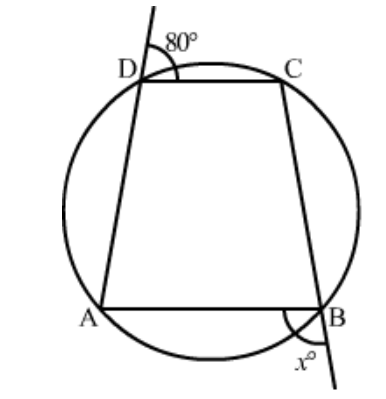
In cyclic quadrilateral the sum of opposite angles is equal to $180^{\circ}$.

Therefore,

$\angle A D C+\angle A B C=180^{\circ}$

$\Rightarrow 180^{\circ}-80^{\circ}+180^{\circ}-x=180^{\circ}$

$\Rightarrow x=100^{\circ}$

Hence, the value of $x$ is $100^{\circ}$.

Question 18: $A B C D$ is a cyclic quadrilateral in which:

(i) $B C \| A D, \angle A D C=110^{\circ}$ and $\angle B A C=50^{\circ} .$ Find $\angle D A C$.

(ii) $\angle D B C=80^{\circ}$ and $\angle B A C=40^{\circ} .$ Find $\angle B C D$.

(iii) $\angle B C D=100^{\circ}$ and $\angle A B D=70^{\circ}$ find $\angle A D B$.

Solution. (i) It is given that $B C \| A D, \angle A D C=110^{\circ}$ and $\angle B A C=50^{\circ}$



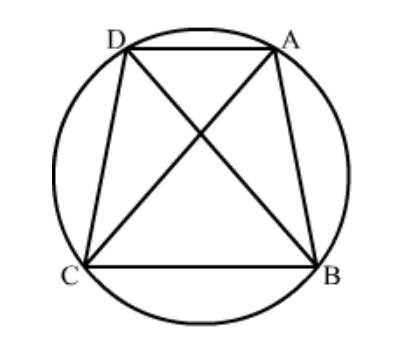
We have to find $\angle D A C$

In cyclic quadrilateral $A B C D$

$\angle A+\angle C=180^{\circ} \ldots . .(1)$

$\angle B+\angle D=180^{\circ} \ldots$(2)

Since, $\angle A D C=110^{\circ}$

So,

$\angle B=180^{\circ}-\angle D$

$=180^{\circ}-110^{\circ}$

$=70^{\circ}$

Therefore in $\triangle A B C, 50^{\circ}+70^{\circ}+\angle B C A=180^{\circ}$

So, $\angle B C A=60^{\circ} \ldots \ldots$ (3)

Now, $\angle B C A=\angle C A D$

( $B C \| A D$ and $A C$ is transversal)

$\Rightarrow \angle B C A=\angle C A D=60^{\circ}$

(ii) It is given that $B C \| A D, \angle D B C=80^{\circ}$ and $\angle B A C=40^{\circ}$

We have to find $\angle B C D$

$\angle B A C=\angle B D C=40^{\circ}$

(Angle in the same segment are equal)

$\angle D C B=180^{\circ}-\left(80^{\circ}+40^{\circ}\right)$

$=180^{\circ}-120^{\circ}$

$=60^{\circ}$

Hence, $\angle B C D=60^{\circ}$

(iii) It is given that, $\angle B C D=100^{\circ}$ and $\angle A B D=70^{\circ}$

As we know that sum of the opposite pair of angles of cyclic quadrilateral is $180^{\circ}$.

$\angle D A B+\angle B C D=180^{\circ}$

$\Rightarrow \angle D A B=180^{\circ}-100^{\circ}$

$=80^{\circ}$

In $\triangle A B D$ we have,

$\angle D A B+\angle A B D+\angle B D A=180^{\circ}$

$\Rightarrow \angle B D A=180^{\circ}-150^{\circ}=30^{\circ}$

Hence, $\angle A B D=30^{\circ}$

Question 19: Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.

Solution. Here, $A B C D$ is a rhombus; we have to prove the four circles described on the four sides of any rhombus $A B C D$ pass through the point of intersection of its diagonals $A C$ and $B D$.



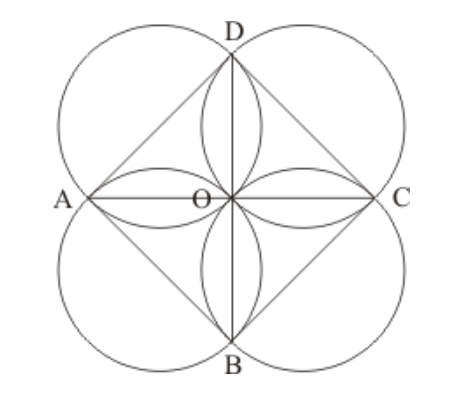
Let the diagonals $A C$ and $B D$ intersect at $O$.

We know that the diagonals of a rhombus intersect at right angle.

Therefore,

$\angle A O B=90^{\circ}$

$\angle B O C=90^{\circ}$

$\angle C O D=90^{\circ}$

$\angle A O D=90^{\circ}$

Now, $\angle A O B=90$ means that circle described on $A B$ as diameter passes through $O$.

Similarly the remaining three circles with $B C, C D$ and $A D$ as their diameter will also pass through $O$.

Hence, all the circles with described on the four sides of any rhombus $A B C D$ pass through the point of intersection of its diagonals $A C$ and $B D$.

Question 20: If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.

Solution.



To prove: $A C=B D$

Proof: We know that equal chords subtend equal at the centre of circle and the angle subtended by a chord at the centre is twice the angle subtended by it at remaining part of the circle.

$\angle A O D=\angle B O C$

$(O$ is the centre of the circle)

$\angle A O D=2 \angle A C D$

and $\angle B O C=2 \angle B D C$

Since, $\angle A O D=\angle B O C$

$\Rightarrow \angle A C D=\angle B D C \quad \ldots$(1)

$\angle A C B=\angle A D B$ $\ldots$(2)

(Angle in the same segment are equal)

Adding $(1)$ and $(2)$

$\angle B C D=\angle A D C$ $\ldots \ldots(3)$

In $\triangle A C D$ and $\triangle B D C$

$C D=C D \quad$ (common)

$\angle B C D=\angle A D C \quad[\mathrm{Using}(3)]$

$A D=B C \quad$ (given)

Hence, $\triangle A C D \cong B D C \quad$ (SAS congruency criterion)

$\therefore A C=B D \quad(\mathrm{cpct})$

Hence Proved

Question 21: Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).

Solution.



$\angle A D B=90^{\circ}$

(Angle in a semicircle)

$\angle A D C=90^{\circ}$

(Angle in a semicircle)

So, $\angle A D B+\angle A D C=90^{\circ}+90^{\circ}=180^{\circ}$

Therefore, $B D C$ is a line.

Hence, the point of intersection of two circles lie on the third side.



Question 22: $A B C D$ is a cyclic trapezium with $A D \| B C$. If $\angle B=70^{\circ}$, determine other three angles of the trapezium.

Solution. If in cyclic quadrilateral $\angle B=70^{\circ}$, then we have to find the other three angles.



Since, $A D$ is parallel to $B C$, So,

$\angle B+\angle A=180$

(Alternate interior angles)

$70+\angle A=180$

$\Rightarrow \angle A=180-70=110^{\circ}$

Now, since $A B C D$ is cyclic quadrilateral, so

$\angle A+\angle C=180$

$\Rightarrow 110+\angle C=180$

$\Rightarrow \angle C=180-110=70^{\circ}$

And,

$\angle B+\angle D=180$

$\Rightarrow 70+\angle D=180$

$\Rightarrow \angle D=180-70=110^{\circ}$

Hence, $\angle A=110^{\circ}, \angle C=70^{\circ}$ and $\angle D=110^{\circ}$.

Question 23: In the given figure, $A B C D$ is a cyclic quadrilateral in which $A C$ and $B D$ are its diagonals. If $\angle D B C=$ $55^{\circ}$ and $\angle B A C=45^{\circ}$, find $\angle B C D$.



Solution. It is given that $A B C D$ is a cyclic quadrilateral with $A C$ and $D B$ as its diagonals.



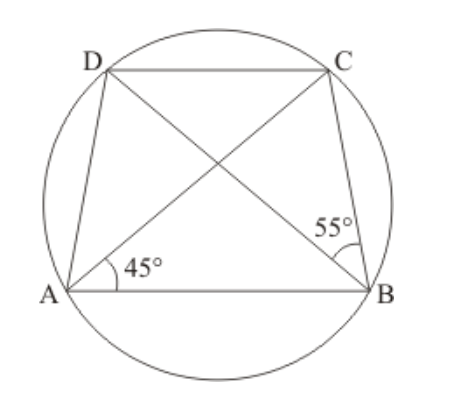
We have to find $\angle B C D$

Since angles in the same segment of a circle are equal

So $\angle C A D=\angle D B C=55^{\circ}$

$\angle D A B=\angle C A D+\angle B A C$

$=55^{\circ}+45^{\circ}$

$=100^{\circ}$

Since $\angle D A B+\angle B C D=180^{\circ}$ (Opposite angle of cyclic quadrilateral)

$\angle B C D=180^{\circ}-100^{\circ}$

$=80^{\circ}$

Hence $\angle B C D=80^{\circ}$

Question 24: Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.

Solution.



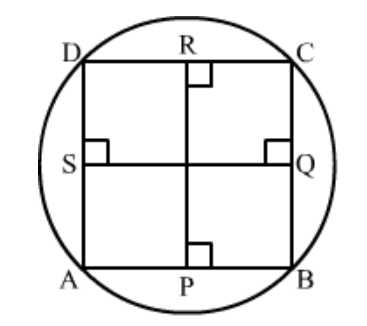
To prove: Perpendicular bisector of side $A B, B C, C D$ and $D A$ are concurrent i.e, passes through the same point.

Proof:

We know that the perpendicular bisector of every chord of a circle always passes through the centre.

Therefore, Perpendicular bisectors of chord $A B, B C, C D$ and $D A$ pass through the centre which means they all passes through the same point.

Hence, the perpendicular bisector of $A B, B C, C D$ and $D A$ are concurrent.

Question $25:$ Prove that the centre of the circle circumscribing the cyclic rectangle $A B C D$ is the point of intersection of its diagonals.

Solution. Here, $A B C D$ is a cyclic rectangle; we have to prove that the centre of the corresponding circle is the intersection of its diagonals.



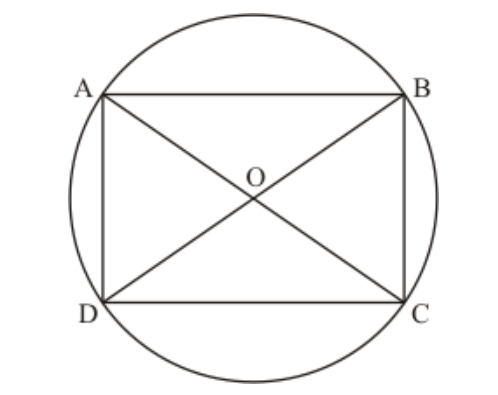
Let $O$ be the centre of the circle.

We know that the angle formed in the semicircle is $90^{\circ}$.

Since, $A B C D$ is a rectangle, So

$\angle A D C=\angle D C B=\angle A B C=\angle B A D=90^{\circ}$

Therefore, $A C$ and $B D$ are diameter of the circle.

We also know that the intersection of any two diameter is the centre of the circle.

Hence, the centre of the circle circumscribing the cyclic rectangle $A B C D$ is the point of intersection of its diagonals.

Question 26: $A B C D$ is a cyclic quadrilateral in which $B A$ and $C D$ when produced meet in $E$ and $E A=E D$. Prove that:

(i) $A D \| B C$

(ii) $E B=E C$

Solution. (i) If $A B C D$ is a cyclic quadrilateral in which $A B$ and $C D$ when produced meet in $E$ such that $E A=E D$, then we have to prove the following, $A D \| B C$

(ii) $E B=E C$



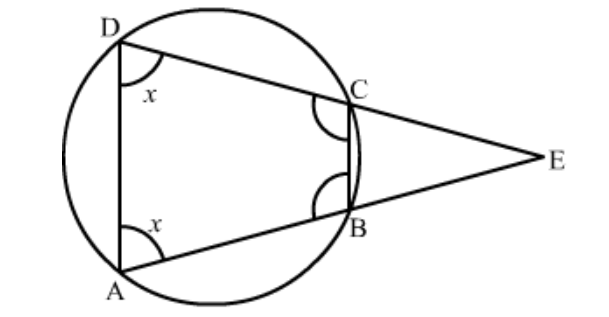
(i) It is given that $E A=E D$, so

$\angle E A D=\angle E D A=x$

Since, $A B C D$ is cyclic quadrilateral

$x+\angle A B C=180 \Rightarrow \angle D A B=180-x$

And; $x+\angle B C D=180 \Rightarrow \angle B C D=180-x$

Now,

$\angle D A B+\angle A B C=x+180-x=180$

Therefore, the adjacent angles $\angle D A B$ and $\angle A B C$ are supplementary

Hence, $A D \| B C$

(ii) Since, $A D$ and $B C$ are parallel to each other, so,

$\angle E C B=\angle E D A \quad$ (Corresponding angles)

$\angle E B C=\angle E A D \quad$ (Corresponding angles)

But, $\angle E D A=\angle E A D$

Therefore, $\angle E C B=\angle E B C$

$\Rightarrow E C=E B$

Therefore, $\triangle E C B$ is an isosceles triangle.

Question $27:$Prove that the angle in a segment shorter than a semicircle is greater than a right angle.

Solution.



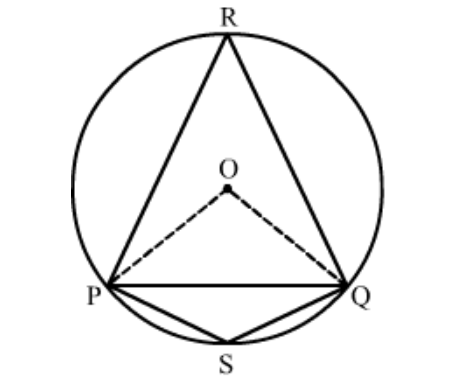
$\overbrace{Q P}$ is a major arc and $\angle P S Q$ is the angle formed by it in the alternate segment.

We know that the angle subtended by an arc at the centre is twice the

angle subtended by it at any point of the alternate segment of the circle.

$\therefore 2 \angle P S Q=m(\overbrace{Q P})$

$\Rightarrow 2 \angle P S Q=360^{\circ}-m(\overbrace{P Q})$

$\Rightarrow 2 \angle P S Q=360^{\circ}-\angle P O Q$

$\Rightarrow 2 \angle P S Q=360^{\circ}-180^{\circ} \quad\left(\because \angle P O Q<180^{\circ}\right)$

$\Rightarrow 2 \angle P S Q>180^{\circ}$

$\Rightarrow \angle P S Q>90^{\circ}$

Thus, the angle in a segment shorter than a semi-circle is greater than a right angle.

Question 28: Prove that the angle in a segment greater than a semi-circle is less than a right angle.

Solution.



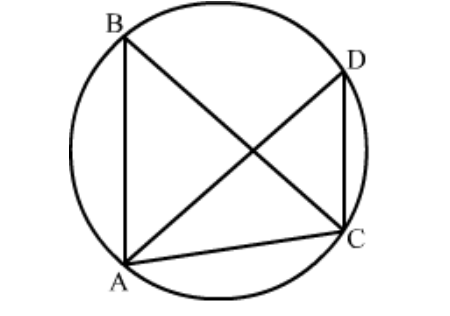
To prove : $\angle A B C$ is an acute angle

Proof:

$A D$ being the diameter of the given circle

$\Rightarrow \angle A C D=90^{\circ} \quad[$ Angle in a semicircle is a right angle $]$

Now, in $\triangle A C D, \angle A C D=90^{\circ}$ which means that $\angle A D C$ is an acute angle. $\ldots \ldots(1)$

Again, $\angle A B C=\angle A D C \quad[$ Angle in a same segment are always equal]

$\Rightarrow \angle A B C$ is also an acute angle. $[\mathrm{Using}(1)]$

Hence proved

Question 29: Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.

Solution. We have to prove that $B P=\frac{1}{2} A C$



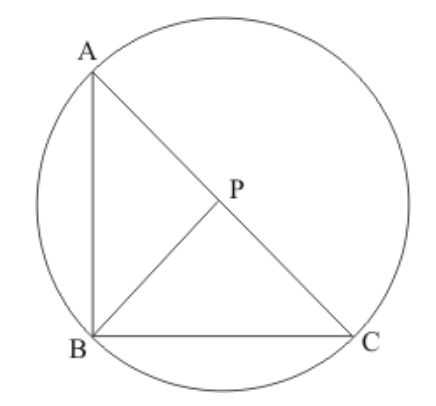
Let $\Delta A B C$ be a right angle at $\mathrm{B}$ and $P$ be midpoint of $A C$

Draw a circle with center at $P$ and $A C$ diameter

Since $\angle A B C=90^{\circ}$ therefore circle passing through $B$

So $B P=C P=$ radius

$\Rightarrow A P=B P=C P$

Hence

$B P=\frac{1}{2} A C$ Proved.

Question 1: If the length of a chord of a circle is $16 \mathrm{~cm}$ and is at a distance of $15 \mathrm{~cm}$ from the centre of the circle, then the radius of the circle is

(a) $15 \mathrm{~cm}$

(b) $16 \mathrm{~cm}$

(c) $17 \mathrm{~cm}$

(d) $34 \mathrm{~cm}$

Solution. (c) $17 \mathrm{~cm}$

We will represent the given data in the figure



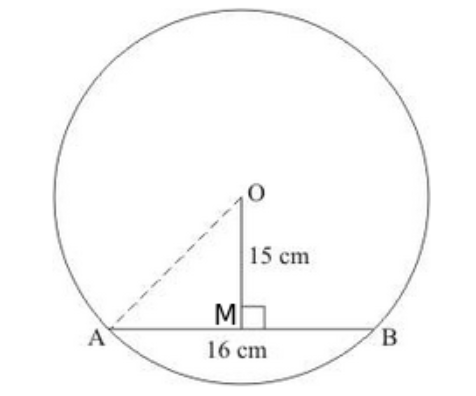
In the diagram $A B$ is the given chord of $16 \mathrm{~cm}$ length and $O M$ is the perpendicular distance from the centre to $A B$.

We know that perpendicular from the centre to any chord divides it into two equal parts.

So, $A M=M B=\frac{16}{2}=8 \mathrm{~cm}$

Now consider right triangle $O M A$ and by using Pythagoras theorem

$A O^{2}=A M^{2}+O M^{2}$

$=8^{2}+15^{2}$

$=64+225$

$=289$

$=\sqrt{289}$

$=17 \mathrm{~cm}$

Hence, correct answer is option (c).

Question 2: The radius of a circle is $6 \mathrm{~cm}$. The perpendicular distance from the centre of the circle to the chord which is $8 \mathrm{~cm}$ in length, is

(a) $\sqrt{5} \mathrm{~cm}$

(b) $2 \sqrt{5} \mathrm{~cm}$

(c) $2 \sqrt{7} \mathrm{~cm}$

(d) $\sqrt{7} \mathrm{~cm}$

Solution. (b) $2 \sqrt{5} \mathrm{~cm}$

We will represent the given data in the figure



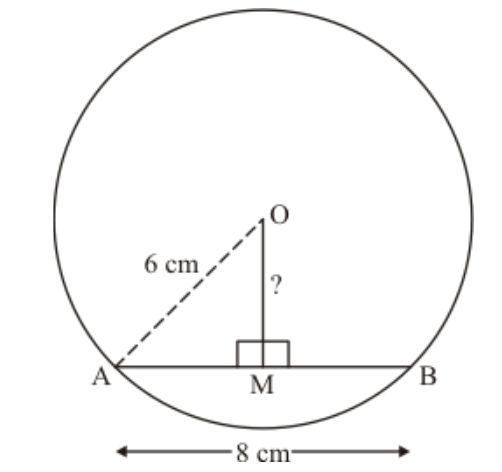
We know that perpendicular drawn from the centre to the chord divides the chord into two equal parts.

So,$A M=M B=\frac{A B}{2}=\frac{8}{2}=4 \mathrm{~cm}$

Using Pythagoras theorem in the $\triangle A M O$,

$O M^{2}=A O^{2}-A M^{2}$

$=6^{2}-4^{2}$

$=36-16$

$=\sqrt{20}$

$=2 \sqrt{5} \mathrm{~cm}$

Hence, the correct answer is option (b).

Question 3: If $\mathrm{O}$ is the centre of a circle of radius $\mathrm{r}$ and $\mathrm{AB}$ is a chord of the circle at a distance $\mathrm{r} / 2$ from $\mathrm{O}$, then $\angle \mathrm{BAO}=$

(a) $60^{\circ}$

(b) $45^{\circ}$

(c) $30^{\circ}$

(d) $15^{\circ}$

Solution. We will associate the given information in the following figure.



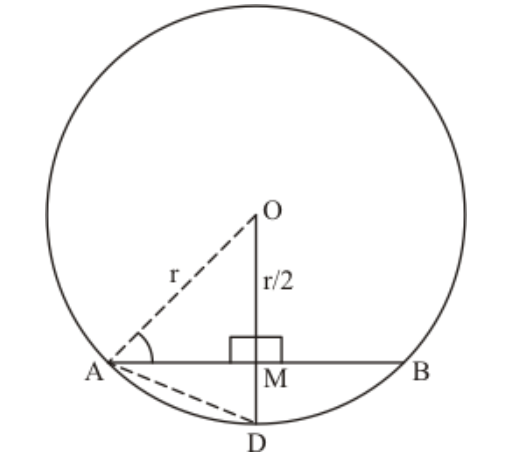
Since $A O=r$ (radius of circle)

$A M=\frac{r}{2}($ given $)$

Extended $O M$ to $D$ where $M D=\frac{r}{2}$

Consider the triangles $A O M$ and triangle $A M D$

$O M=M D$

$\angle A M O=\angle A M D=90^{\circ}$

$A M=A M$

(Common Sides)

So by SSS property

$\Delta A M O \cong \Delta A D M$

So $A D=A O=r$ and $O D=O M+M D=r$

Hence $\triangle A O D$ is equilateral triangle

So $\angle O A D=60^{\circ}$

We know that in equilateral triangle altitudes divide the vertex angles

Therefore

$\angle O A M=\frac{\angle O A D}{2}$

$=\frac{60}{2}$

$=30^{\circ}$

Hence option $(c)$ is correct.

Question 4: $A B C D$ is a cyclic quadrilateral such that $\angle A D B=30^{\circ}$ and $\angle D C A=80^{\circ}$, then $\angle D A B=$

(a) $30^{\circ}$

(b) $60^{\circ}$

(c) $90^{\circ}$

(d) $120^{\circ}$

Solution. (d) $120^{\circ}$

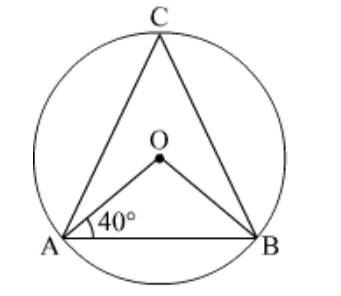
We are given that an equilateral $\triangle A B C$ is inscribed in a circle with centre $O$. We need to find $\angle B O C$

We have the following corresponding figure:



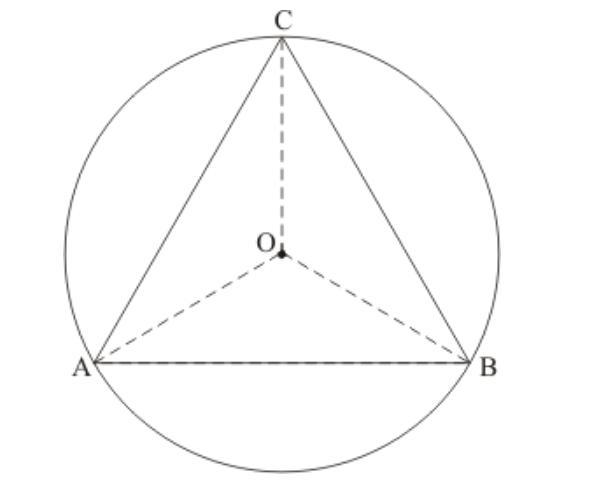
We are given $A B=B C=A C$

Since the sides $A B, B C$, and $A C$ are these equal chords of the circle.

So, the angle subtended by these chords at the centre will be equal.

Hence

$\angle A O B+\angle B O C+\angle A O C=360$

$\angle B O C+\angle B O C+\angle B O C=360$

$3 \angle B O C=360$

$\angle B O C=\frac{360}{3}$

$\angle B O C=120^{\circ}$

Hence, the correct answer is option (d).

Question 13: If two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a

(a) rhombus

(b) rectangle

(c) parallelogram

(d) square

Solution. (d) square

The given information in the form of the following figure is as follows:



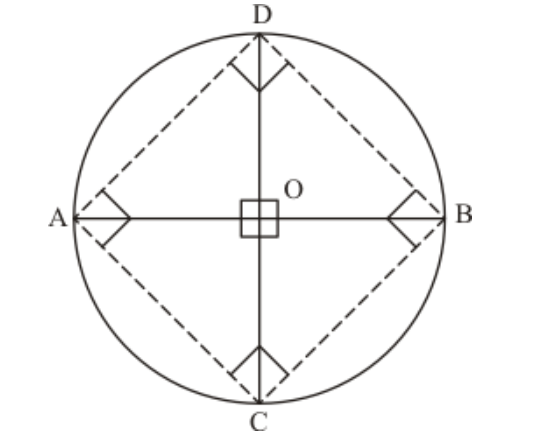
Since, four sides of the quadrilateral $A C B D$ are four chords which subtend equal angles at the centre. Therefore,

$\angle A O C=\angle C O B=\angle B O D=\angle D O A=90^{\circ}$

(Since $A B$ and $C D$ are perpendicular diameters)

So sides $A C, B C, B D$ and $A D$ are equal, as equal chords subtend equal angle at the centre.

So,$A C=C B=B D=D A$ $\ldots \ldots$ (1)$

We know that diameters subtend an angle of measure $90^{\circ}$ on the circle.

So, $\angle A C B=\angle C B D=\angle B D A=\angle D A C=90^{\circ} \ldots$(2)

From (1) and (2) we can say that $\square$ ACBD is a square.

Hence, the correct answer is option (d).

Question 14: If $A B C$ is an arc of a circle and $\angle A B C=135^{\circ}$, then the ratio of arc $\overbrace{A B C}$ to the circumference is

(a) $1: 4$

(b) $3: 4$

(c) $3: 8$

(d) $1: 2$

Solution. (c) $3: 8$

The length of an arc subtending an angle ' $\theta^{\prime}$ in a circle of radius ${ }^{‘} r$ ' is given by the formula.

Length of the $\operatorname{arc}=\frac{\theta}{360^{\circ}} 2 \pi r$

Here, it is given that the arc subtends an angle of $135^{\circ}$ with its centre. So the length of the given arc in a circle with radius ' $r$ ' is given as

Length of the $\operatorname{arc}=\frac{135^{\circ}}{360^{\circ}} 2 \pi r$

The circumference of the same circle with radius ' $r$ ' is given as $2 \pi r$.

The ratio between the lengths of the arc and the circumference of the circle will be,

$\frac{\text { Length of the arc }}{\text { Circumference of the circle }}=\frac{135^{\circ}(2 \pi r)}{360^{\circ}(2 \pi r)}$

$=\frac{135^{\circ}}{360^{\circ}}$

$=\frac{3}{8}$

Hence, the correct answer is option (c).

Question 15: The chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is

(a) $60^{\circ}$

(b) $75^{\circ}$

(c) $120^{\circ}$

(d) $150^{\circ}$

Solution. (d) $150^{\circ}$

We are given that the chord is equal to its radius.

We have to find the angle subtended by this chord at the minor arc.

We have the corresponding figure as follows:



We are given that

$A O=O B=A B$

So , $\triangle A O B$ is an equilateral triangle.

Therefore, we have

$\angle A O B=60^{\circ}$

Since, the angle subtended by any chord at the centre is twice of the angle subtended at any point on the circle.

So $\quad \angle A Q B=\frac{\angle A O B}{2}$

$=\frac{60}{2}=30^{\circ}$

Take a point $P$ on the minor arc.

Since $\square A P B Q$ is a cyclic quadrilateral

So, opposite angles are supplementary. That is

$\angle A P B+\angle A Q B=180^{\circ}$

$\angle A P B+30^{\circ}=180^{\circ}$

$\angle A P B=180^{\circ}-30^{\circ}$

$=150^{\circ}$

Hence, the correct answer is option (d).

Question 16: $P Q R S$ is a cyclic quadrilateral such that $P R$ is a diameter of the circle. If $\angle Q P R=67^{\circ}$ and $\angle S P R=$ $72^{\circ}$, then $\angle Q R S=$

(a) $41^{\circ}$

(b) $23^{\circ}$

(c) $67^{\circ}$

(d) $18^{\circ}$

Solution. Here we have a cyclic quadrilateral $P Q R S$ with $P R$ being a diameter of the circle. Let the centre of this circle be ' $O$ '.

We are given that $\angle Q P R=67^{\circ}$ and $\angle S P R=72^{\circ}$. This is shown in fig $(2)$.



So we see that,

$\angle Q P S=\angle Q P R+\angle R P S$

$=67^{\circ}+72^{\circ}$

$-139^{\circ}$

(a) $41^{\circ}$

In a cyclic quadrilateral it is known that the opposite angles are supplementary.

$\angle Q P S+\angle Q R S=180^{\circ}$

$\angle Q R S=180^{\circ}-\angle Q P S$

$=180^{\circ}-139$

$=41^{\circ}$

Hence the correct answer is option (a).

Question 17: If $A, B, C$ are three points on a circle with centre $O$ such that $\angle A O B=90^{\circ}$ and $\angle B O C=120^{\circ}$, then $\angle A B C=$

(a) $60^{\circ}$

(b) $75^{\circ}$

(c) $90^{\circ}$

(d) $135^{\circ}$

Solution. (b) $75^{\circ}$

To solve this problem we need to know that the angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.



Here we are given that ' $A$ ', ' $B$ ', ' $C$ ' are three points on a circle with centre ' $O$ ' such that $\angle A O B=90^{\circ}$ and $\angle B O C=120^{\circ}$.

From the figure we see that,

$\angle A O C=360^{\circ}-\angle A O B-\angle B O C$

$=360^{\circ}-90^{\circ}-120^{\circ}$

$=360^{\circ}-210^{\circ}$

$=150^{\circ}$

Now, as seen earlier, the angle made by the arc ' $A C$ ' with the centre of the circle will be twice the angle it makes in any point in the remaining part of the circle.

Since the point ' $C$ ' lies on the remaining part of the circle, the angle the arc ' $A C$ makes with this point has to be half of the angle ' $A C$ ' makes with the centre. Therefore we have,

$\angle A B C=\frac{\angle A O C}{2}$

$=\frac{150^{\circ}}{2}$

$=75^{\circ}$

Hence the correct answer is option (b).

Question 18:The greatest chord of a circle is called its

(a) radius

(b) secant

(c) diameter

(d) none of these

Solution. (c) diameter

The greatest chord in a circle is the diameter of the circle.

Hence the correct answer is option (c).

Question 19: Angle formed in minor segment of a circle is

(a) acute

(b) obtuse

(c) right angle

(d) none of these

Solution. (b) obtuse

Whenever a chord is drawn in a circle two segments are formed. One is called the minor segment while the other is called the major segment.

The angle formed by the chord in the minor segment will always be obtuse.

Hence the correct answer is option (b).

Question 20: Number of circles that can be drawn through three non-collinear points is

(a) 1

(b) 0

(c) 2

(d) 3

Solution. (a) 1

Suppose we are given three non-collinear points as $A, B$ and $C$



1. Join A and B.

2. Join B and C.

3. Draw perpendicular bisector of $A B$ and $B C$ which meet at $O$ as centre of the circle.

So basically we can only draw one circle passing through three non-collinear points $A, B$ and $C$.

Hence, the correct answer is option (a).

Question 21: In the given figure, if chords $A B$ and $C D$ of the circle intersect each other at right angles, then $x+y=$

(a) $45^{\circ}$

(b) $60^{\circ}$

(c) $75^{\circ}$

(d) $90^{\circ}$



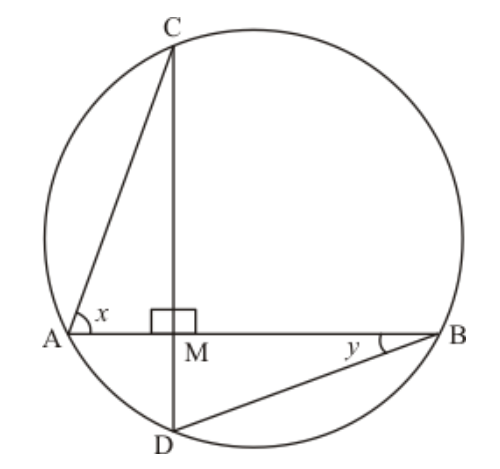
Solution. (d) $90^{\circ}$

We are given the following figure



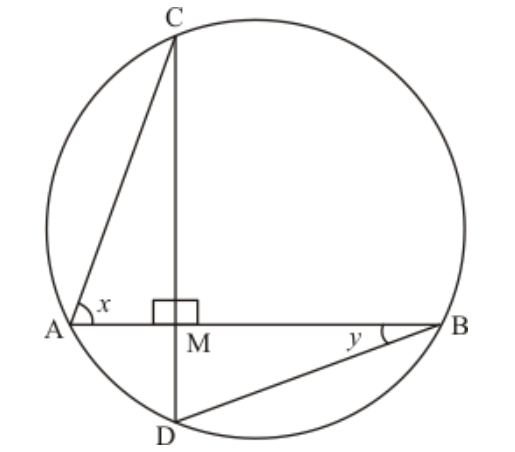
$\angle A C D=\angle A B D$(Angle in the same segment are equal)

$\Rightarrow \angle A C D=y$

Consider the $\triangle A C M$ in which

$\angle A C M+x+90^{\circ}=180^{\circ}$

$y+x+90^{\circ}=180^{\circ}$

$x+y=90^{\circ}$

Hence, the correct answer is option (d).

Question 22: In the given figure, if $\angle A B C=45^{\circ}$, then $\angle A O C=$

(a) $45^{\circ}$

(b) $60^{\circ}$

(c) $75^{\circ}$

(d) $90^{\circ}$



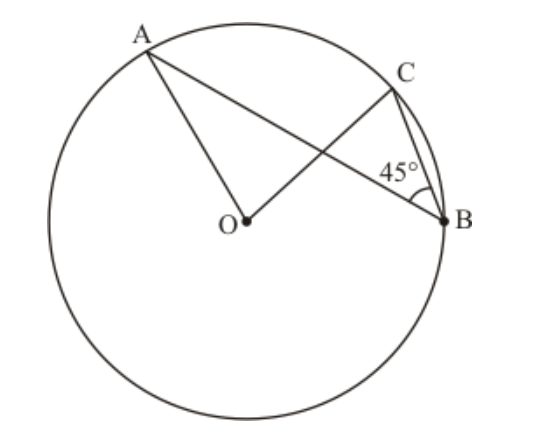
Solution. (d) $90^{\circ}$

We have to find $\angle A O C$.



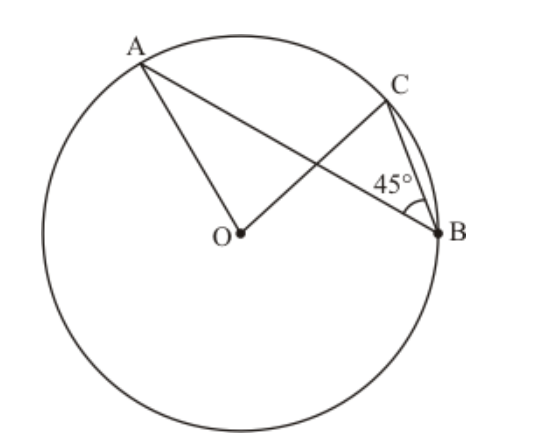
As we know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

$\angle A O C=2 \angle A B C$

$=2 \times 45$

$=90^{\circ}$

Hence, the correct answer is option (d).

Question 23: In the given figure, chords $A D$ and $B C$ intersect each other at right angles at a point $P$. If $\angle D A B=$ $35^{\circ}$, then

$\angle A D C=$

(a) $35^{\circ}$

(b) $45^{\circ}$

(c) $55^{\circ}$

(d) $65^{\circ}$



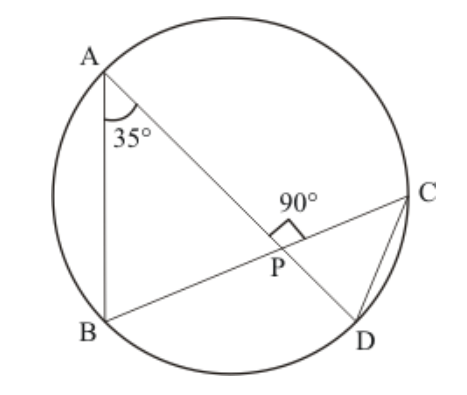
Solution. (c) $55^{\circ}$



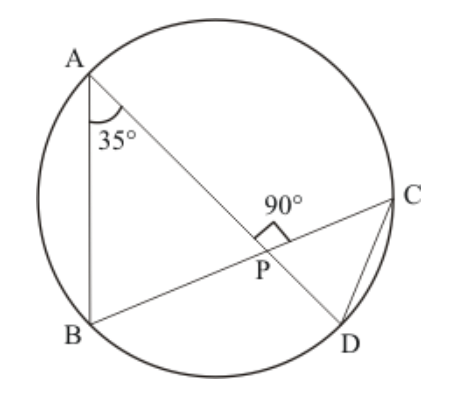
$\angle B A D=\angle B C D=35^{\circ} \quad$ (Angle in the same segment are equal.)

Also, since the chords ' $A D$ ' and ' $B C$ ' intersect perpendicularly we have,

$\angle C P D=90^{\circ}$

Consider the triangle $\Delta C P D$,

$\angle C P D+\angle P D C+\angle P C D=180^{\circ}$

$\angle P D C=180^{\circ}-\angle P C D-\angle C P D$

$=180^{\circ}-35^{\circ}-90^{\circ}$

$=55^{\circ}$

$\angle P D C=\angle A D C=55^{\circ}$

Hence, the correct answer is option (c).

Question 24: In the given figure, $O$ is the centre of the circle and $\angle B D C=42^{\circ}$. The measure of $\angle A C B$ is

(a) $42^{\circ}$

(b) $48^{\circ}$

(c) $58^{\circ}$

(d) $52^{\circ}$



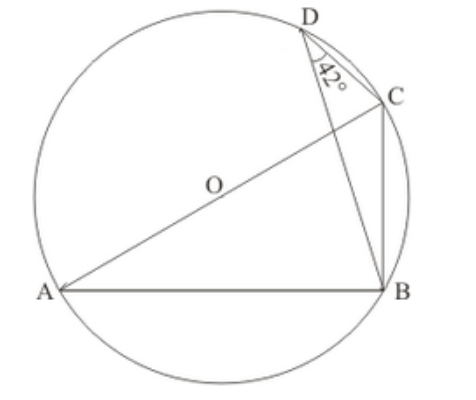
Solution. (b) $48^{\circ}$

Construction: Join A and D.



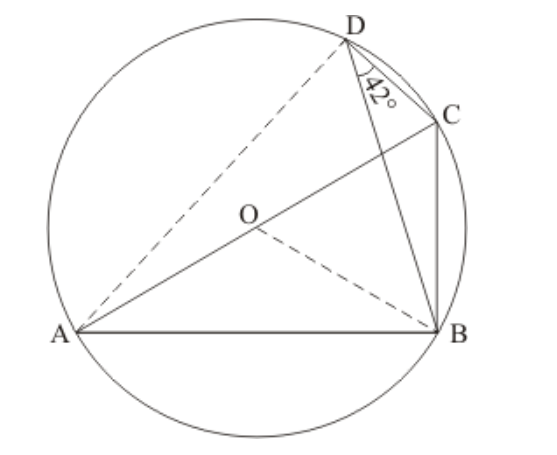
Since $A C$ is the diameter. So $\angle A D C$ will be $90^{\circ}$.

Therefore,

$\angle A D B=90-\angle B D C$

$=90-42$

$\angle A D B=48^{\circ}$

$\angle A C B=\angle A D B=48^{\circ}$

(Angle in the same segment are equal.)

Hence, the correct answer is option (b).

Question 25: In a circle with centre $\mathrm{O}, A B$ and $C D$ are two diameters perpendicular to each other. The length of chord $A C$ is

(a) $2 A B$

(b) $\sqrt{2}$

(c) $\frac{1}{2} A B$

(d) $\frac{1}{\sqrt{2}} A B$

Solution. (d) $\frac{1}{\sqrt{2}} A B$

We are given a circle with centre at $O$ and two perpendicular diameters $A B$ and $C D$.

We need to find the length of $A C$.

We have the following corresponding figure:



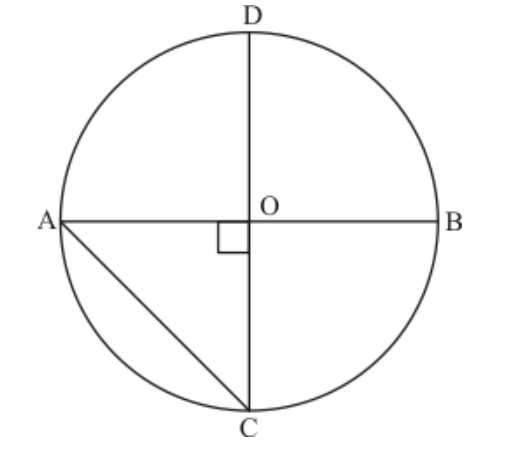
Since, $A B=C D$ (Diameter of the same circle)

Also, $\angle A O C=90^{\circ}$

And, $A O=\frac{A B}{2}$

Here, $A O=O C$ (radius)

In $\triangle A O C$

$A C^{2}=A O^{2}+O C^{2}=A O^{2}+A O^{2}$

$=\left(\frac{A B}{2}\right)^{2}+\left(\frac{A B}{2}\right)^{2}$

$A C^{2}=\frac{A B^{2}}{2}$

$A C=\frac{A B}{\sqrt{2}}$

Hence, the correct answer is option (d).

Question 26: Two equal circles of radius $r$ intersect such that each passes through the centre of the other. The length of the common chord of the circle is

(a) $\sqrt{r}$

(b) $\sqrt{2} r A B$

(c) $\sqrt{3} r$

(d) $\frac{\sqrt{3}}{2}$

Solution. (c) $\sqrt{3} r$

We are given two circles of equal radius intersect each other such that each passes through the centre of the other.

We need to find the common chord.

We have the corresponding figure as follows:



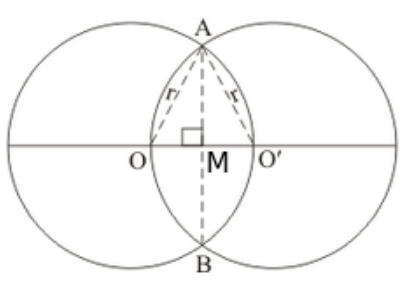
$A O=A O^{\prime}=r$ (radius)

And $O O^{\prime}=r$

So, $\triangle O A O^{\prime}$ is an equilateral triangle.

We know that the attitude of an equilateral triangle with side $r$ is given by $\frac{\sqrt{3} r}{2}$

That is $A M=\frac{\sqrt{3}}{2} r$

We know that the line joining centre of the circles divides the common chord into two equal parts.

So we have

$A B=2 A M$

$=2 \cdot \frac{\sqrt{3}}{2} r$

$A B=\sqrt{3} r$

Hence, the correct answer is option (c).

Question 27: If $A B$ is a chord of a circle, $P$ and $Q$ are the two points on the circle different from $A$ and $B$, then

(a) $\angle A P B=\angle A Q B$

(b) $\angle A P B+\angle A Q B=180^{\circ}$ or $\angle A P B=\angle A Q B$

(c) $\angle A P B+\angle A Q B=90^{\circ}$

(d) $\angle A P B+\angle A Q B=180^{\circ}$

Solution. (b) $\angle A P B+\angle A Q B=180^{\circ}$ or $\angle A P B=\angle A Q B$

We are given $A B$ is a chord of the circle; $P$ and $Q$ are two points on the circle different from $A$ and $B$.

We have following figure.

Case 1: Consider $P$ and $Q$ are on the same side of $A B$



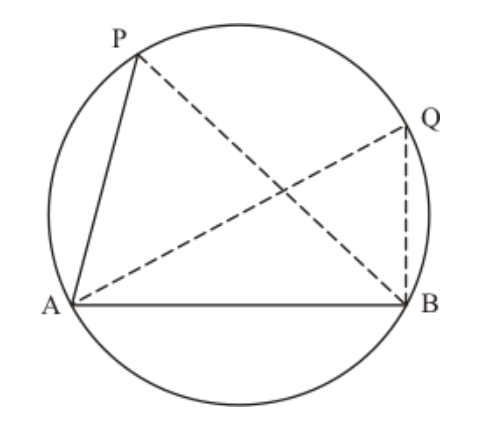
We know that angle in the same segment are equal.

Hence, $\angle A P B=\angle A Q B$

Case 2: Now consider $P$ and $Q$ are on the opposite sides of $A B$

In this case we have the following figure:



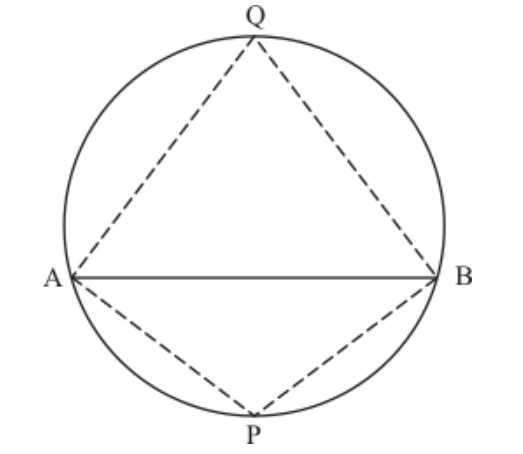
Since quadrilateral $A P B Q$ is a cyclic quadrilateral.

Therefore,

$\angle A P B+\angle A Q B=180^{\circ}$

(Sum of the pair of opposite angles of cyclic quadrilateral is $180^{\circ}$.)

Therefore, $\angle A P B=\angle A Q B$ or $\angle A P B+\angle A Q B=180^{\circ}$

Hence, the correct answer is option (b).

Question 28: $A B$ and $C D$ are two parallel chords of a circle with centre $O$ such that $A B=6 \mathrm{~cm}$ and $C D=12 \mathrm{~cm}$. The chords are on the same side of the centre and the distance between them is $3 \mathrm{~cm}$. The radius of the circle is

(a) $6 \mathrm{~cm}$

(b) $5 \sqrt{2} \mathrm{~cm}$

(c) $7 \mathrm{~cm}$

(d) $3 \sqrt{5} \mathrm{~cm}$

Solution. (d) $3 \sqrt{5} \mathrm{~cm}$

Let distance between the centre and the chord $\mathrm{CD}$ be $x \mathrm{~cm}$ and the radius of the circle is $r \mathrm{~cm}$.

We have to find the radius of the following circle:



In triangle OND.

$x^{2}+36=r^{2} \ldots \cdots$(1)

Now, in triangle AOM,

$r^{2}=9+(x+3)^{2} \ldots \cdots$(2)

From (1) and (2), we have,

$r^{2}=9+\left(\sqrt{r^{2}-36}+3\right)^{2}$

$\Rightarrow r^{2}=9+r^{2}-36+9+6 \sqrt{r^{2}-36}$

$\Rightarrow 3=\sqrt{r^{2}-36}$

$\Rightarrow 9=r^{2}-36$

$\Rightarrow r^{2}=45 \Rightarrow r=3 \sqrt{5}$

Hence, the correct answer is option (d).

Question 29: In a circle of radius $17 \mathrm{~cm}$, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is $23 \mathrm{~cm}$. If the length of one chord is $16 \mathrm{~cm}$, then the length of the other is

(a) $34 \mathrm{~cm}$

(b) $15 \mathrm{~cm}$

(c) $23 \mathrm{~cm}$

(d) $30 \mathrm{~cm}$

Solution. (d) $30 \mathrm{~cm}$

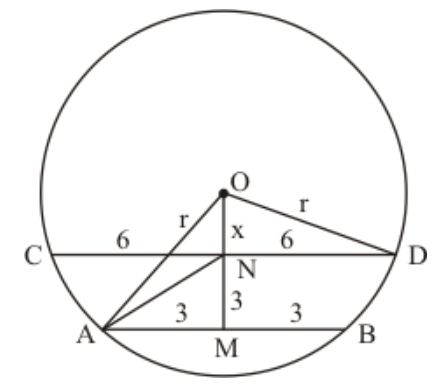
Given that: Radius of the circle is $17 \mathrm{~cm}$, distance between two parallel chords $A B$ and $C D$ is $23 \mathrm{~cm}$, where $A B=16 \mathrm{~cm}$. We have to find the length of $C D$.



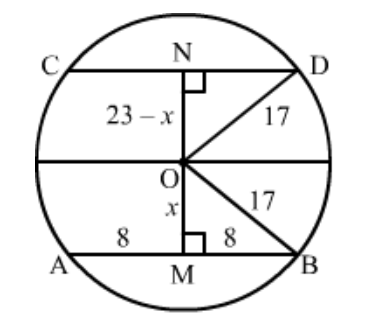
We know that the perpendicular drawn from the centre of the circle to any chord divides it into two equal parts.

So, $A M=M B=8 \mathrm{~cm}$

Let $O M=x \mathrm{~cm}$

In triangle OMB,

$x=\sqrt{17^{2}-8^{2}}=15$

Now, in triangle $\mathrm{OND}, O N=(23-x) \mathrm{cm}=(23-15) \mathrm{cm}=8 \mathrm{~cm}$

$N D=\sqrt{O D^{2}-O N^{2}}$

$\Rightarrow N D=\sqrt{17^{2}-8^{2}}=15$

Therefore, the length of the other chord is

$C D=2 \times 15=30 \mathrm{~cm}$

Hence, the correct answer is option (d).

Question 30: In the given figure, $O$ is the centre of the circle such that $\angle A O C=130^{\circ}$, then $\angle A B C=$

(a) $130^{\circ}$

(b) $115^{\circ}$

(c) $65^{\circ}$

(d) $165^{\circ}$



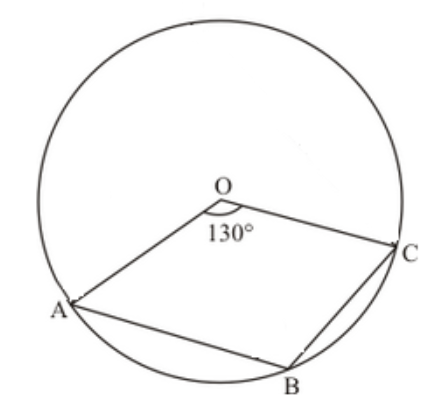
Solution. (b) $115^{\circ}$

We have the following information in the following figure. Take a point $P$ on the circle in the given figure and join $A P$ and $C P$.



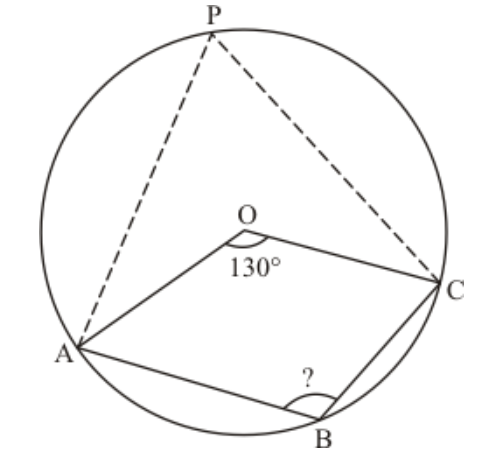
Since, the angle subtended by a chord at the centre is twice that of subtended atany part of the circle.

So, $\angle A P C=\frac{\angle A O C}{2}=\frac{130}{2}=65^{\circ}$

Since $\square A P B P$ is a cyclic quadrilateral and we known that opposite angles are supplementary.

Therefore,

$\angle A B C+\angle A P C=180^{\circ}$

$\Rightarrow \angle A B C+65^{\circ}=180^{\circ}$

$\Rightarrow \angle A B C=180^{\circ}-65^{\circ}$

$\Rightarrow \angle A B C=115^{\circ}$

Hence, the correct answer is optoon (b).

Question 1: Fill In The Blanks

$A D$ is a diameter, of circle and $A B$ is chord. If $A D=34 \mathrm{~cm}, A B=30 \mathrm{~cm}$, then $B D=$_____________.

Solution. Given:

$A D$ is a diameter

$A B$ is chord

$A D=34 \mathrm{~cm}$

$A B=30 \mathrm{~cm}$

Let $O$ be the centre of the circle.

$A O=O D=17 \mathrm{~cm}\ldots(1)$

Let $O L$ is a line perpendicular to $A B$, where $L$ is the point on $A B$.

Then, $A L=L B=15 \mathrm{~cm}\ldots(2)$

( : a perpendicular from the centre of the circle to the chord, bisects the chord)

In $\Delta A L O$

Using pythagoras theorem,

$A L^{2}+\angle O^{2}=A O^{2}$

$\Rightarrow 15^{2}+L O^{2}=17^{2}$

$($ From $(1)$ and $(2))$

$\Rightarrow 225+\angle O^{2}=289$

$\Rightarrow \angle O^{2}=289-225$

$\Rightarrow \angle O^{2}=64$

$\Rightarrow \angle O=8 \mathrm{~cm}$

Now, In $\triangle A B D$

Using mid-point theorem: The line segment joining the mid-points of two sides of a triangle is parallel to the third side and is equal to the half of it.

Therefore, $L O=\frac{1}{2} B D$

$\Rightarrow B D=2 \angle O$

$\Rightarrow B D=2(8)$

$\Rightarrow B D=16 \mathrm{~cm}$

Hence, $B D=16 \mathrm{~cm}$.

Question 2: Fill In The Blanks

$A D$ is a diameter of a circle and $A B$ is a chord. If $A D=34 \mathrm{~cm}, A B=30 \mathrm{~cm}$, then the distance of $A B$ from the centre of the circle is___________.

Solution. Given:

$A D$ is a diameter

$A B$ is chord

$A D=34 \mathrm{~cm}$

$A B=30 \mathrm{~cm}$

Let $O$ be the centre of the circle.

$A O=O D=17 \mathrm{~cm}\ldots(1)$

Let $O L$ is a line perpendicular to $A B$, where $L$ is the point on $A B$.

Then, $A L=L B=15 \mathrm{~cm}\ldots(2)$

(:: a perpendicular from the centre of the circle to the chord, bisects the chord)

In $\Delta A L O$

Using pythagoras theorem,

$A L^{2}+\angle O^{2}=A O^{2}$

$\Rightarrow 15^{2}+L O^{2}=17^{2} \quad($ From $(1)$ and $(2))$

$\Rightarrow 225+\angle O^{2}=289$

$\Rightarrow \angle O^{2}=289-225$

$\Rightarrow L O^{2}=64$

$\Rightarrow \angle O=8 \mathrm{~cm}$

Thus, the distance of the chord from the centre is $8 \mathrm{~cm}$.

Hence, the distance of $A B$ from the centre of the circle is $8 \mathrm{~cm}$.

Question 3: Fill In The Blanks

If $A B=12 \mathrm{~cm}, B C=16 \mathrm{~cm}$, and $A B$ is perpendicular to $B C$, then the radius of the circle passing through the points $A, B$ and $C$ is________.

Solution. Given:

$A B=12 \mathrm{~cm}$

$B C=16 \mathrm{~cm}$

$A B$ is perpendicular to $B C$

Since, $A B$ is perpendicular to $B C$

Therefore, the circle formed by joining $A, B$ and $C$ is a circle with diameter $A C$.

In $\Delta A B C$

Using pythagoras theorem,

$A B^{2}+B C^{2}=A C^{2}$

$\Rightarrow 12^{2}+16^{2}=A C^{2}$ (given)

$\Rightarrow 144+256=A C^{2}$

$\Rightarrow A C^{2}=400$

$\Rightarrow A C=20$

Thus, the diameter of the circle is $20 \mathrm{~cm}$.

Therefore, the radius of the circle is half of the diameter of the circle.

Radius $=\frac{1}{2}(20)=10 \mathrm{~cm}$

Hence, the radius of the circle passing through the points $A, B$ and $C$ is $10 \mathrm{~cm}$.

Question 4: Fill In The Blanks

$A B C D$ is a cyclic quadrilateral such that $A B$ is a diameter of the circle circumscibing it and $\angle A D C=$ $140^{\circ}$, then $\angle B A C=$__________.

Solution. Given:

$A B C D$ is a cyclic quadrilateral

$A B$ is a diameter of the circle circumscribing $A B C D$

$\angle A D C=140^{\circ}$

In a cyclic quadrilateral, the sum of opposite angles is $180^{\circ}$.

Thus, $\angle A D C+\angle A B C=180^{\circ}$

$\Rightarrow 140^{\circ}+\angle A B C=180^{\circ}$

$\Rightarrow \angle A B C=180^{\circ}-140^{\circ}$

$\Rightarrow \angle A B C=40^{\circ}$$\ldots(1)$

Since $A B$ is the diameter of the circle

Therefore, $\angle A C B=90^{\circ}$ (angle in the semi circle) $\ldots(2)$

In $\Delta A B C$

$\angle B A C+\angle A C B+\angle A B C=180^{\circ}$ (angle sum property)

$\Rightarrow \angle B A C+90^{\circ}+40^{\circ}=180^{\circ}($ From $(1)$ and $(2))$

$\Rightarrow \angle B A C+130^{\circ}=180^{\circ}$

$\Rightarrow \angle B A C=180^{\circ}-130^{\circ}$

$\Rightarrow \angle B A C=50^{\circ}$

Hence, $\angle B A C=\underline{50}^{\circ}$

Question 5: Fill In The Blanks

Two chords $A B$ and $C D$ of a circle are each at a distance of $6 \mathrm{~cm}$ from the centre. the ratio of their lengths is________.

Solution. Given:

Two chords $A B$ and $C D$ of a circle are each at a distance of $6 \mathrm{~cm}$ from the centre.

The chords which are equidistant from the centre of the circle are of equal length.

Hence, the ratio of their length is $1: 1$.

Question 6: Fill In The Blanks

If two equals chords $A B$ and $A C$ of a circle with centre $O$ are on the opposite sides of $O A$, then $\angle O A B$ $=$__________.

Solution. Given:

$A B=A C$

$A B$ and $A C$ lies on the opposite sides of $O A$

The chords of equal length, are equidistant from the centre of the circle.

In $\Delta O A B$ and $\triangle O A C$,

$A B=A C$ (given)

$O A=O A$ (common)

$O B=O C$ (radius of the circle)

By SSS property,

$\Delta O A B \cong \Delta O A C$

Therefore, $\angle O A B=\angle O A C$ (by C.P.C.T.)

Hence, $\angle O A B=\angle O A C$.

Question 7: Fill In The Blanks

Two congruent circle with centres $\mathrm{O}$ and $\mathrm{O}$ ' intesect at two points $P$ and $Q$. then then, $\angle P O Q: \angle P O^{\prime} Q=$_________.

Solution. Given:

Two congruent circle with centres $O$ and $O$ ' intersect at two points $P$ and $Q$.

In $\triangle O P Q$ and $\triangle O^{\prime} P Q$,

$O P=O^{\prime} P$ (radius)

$P Q=P Q$ (common)

$\mathrm{OQ}=\mathrm{O}^{\prime} \mathrm{Q}$ (radius)

By SSS property,

$\Delta O P Q \cong \Delta O^{\prime} P Q$

Therefore, $\angle P O Q=\angle P O^{\prime} Q$ (by C.P.C.T.)

Hence, $\angle P O Q: \angle P O^{\prime} Q=1: 1$ Question 8: Fill In The Blanks

If $A O B$ is a diameter of a circle and $C$ is a point on the circle, then the $A C^{2}+B C^{2}=$___________.

Solution. Given:

$A O B$ is a diameter of a circle

$C$ is a point on the circle

Since, $A O B$ is the diameter of the circle

Therefore, $\angle A C B=90^{\circ}$ (angle in the semi circle) $\cdots$(2)$

In right angled $\triangle A B C$,

Using pythagoras theorem.

$A C^{2}+B C^{2}=A B^{2}$

Hence, $A C^{2}+B C^{2}=\underline{A B}^{2}$

Question 9: Fill In The Blanks

If $O$ is the circumcentre of $\triangle A B C$ and $D$ is the mid-point of the base $B C$, then $\angle B O D=$_____________.

Solution. Given:

$\mathrm{O}$ is the circumcentre of $\triangle A B C$

$D$ is the mid-point of the base $B C$

In $\triangle B O D$ and $\triangle C O D$,

$O B=O C$ (radius)

$B D=C D(D$ is the mid-point of the base $B C)$

$O D=O D($ common $)$

By SSS property,

$\Delta B O D \cong \Delta C O D$

Therefore, $\angle B O D=\angle C O D$ (by C.P.C.T.)

$\Rightarrow \angle B O C=\angle B O D+\angle C O D$

$\Rightarrow \angle B O C=2 \angle B O D$.(1)

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle B O C=2 \angle B A C$

$\Rightarrow 2 \angle B O D=2 \angle B A C$

$\Rightarrow \angle B O D=\angle B A C$

Hence, $\angle B O D=\angle B A C$.

Question 10: Fill In The Blanks

If $O$ is the circumcentre of $\triangle A B C$, then $\angle O B C+\angle B A C=$____________.

Solution. Given:

$O$ is the circumcentre of $\triangle A B C$

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle B O C=2 \angle B A C \ldots(1)$

In $\triangle O B C$,

$O B=O C$ (radius)

Thus, $\angle O B C=\angle O C B$. .(2)

Also, $\angle O B C+\angle O C B+\angle B O C=180^{\circ}$ (angle sum property)

$\Rightarrow 2 \angle O B C+2 \angle B A C=180^{\circ} \quad$ (from $(1)$ and $\left.(2)\right)$

$\Rightarrow \angle O B C+\angle B A C=90^{\circ}$

Hence, $\angle O B C+\angle B A C=\underline{90}^{\circ}$.

Question 11: Fill In The Blanks

A chord of a circle is equal to its radius. The angle subtended by this chord at a point in major segment is________.

Solution. Given: A chord of a circle is equal to its radius

Let $A B$ is a chord and $O$ is the centre of the circle.

$A B=O A=O B(\because$ Chord is equal to the radius)

$\Rightarrow \Delta A B O$ is equilateral triangle

Thus, $\angle A O B=60^{\circ}\ldots(1)$

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle A O B=2 \angle A D B$, where $D$ is any point on the major segment of the circle

$\Rightarrow 2 \angle A D B=60^{\circ} \quad($ from $(1)$ and $(2))$

$\Rightarrow \angle A D B=30^{\circ}$

Hence, the angle subtended by the chord at a point in major segment is $\underline{30^{\circ}}$.

Question 12: Fill In The Blanks

If a pair of opposite sides of a quadrilateral are equal, then its diagonals are____________.

Solution. Given:

A pair of opposite sides of a quadrilateral $A B C D$ are equal.

i.e., $A B=C D$ and $A D=B D$

Then, the quadrilateral can be a parallelogram, a rectangle, rhombus or a square. In all the cases the diagonals bisects each other.

Hence, its diagonals are bisecting.

Question 13: Fill In The Blanks

If $\operatorname{arcs} A X B$ and $C Y D$ of a circle are congruent, then $A B: C D=$___________.

Solution. Given:

Arcs $A X B$ and $C Y D$ of a circle are congruent

We know, if any two arcs are congruent, then their corresponding chords are equal.

Thus, Chord $A B=$ Chord $C D$

Hence, $A B: C D=1: 1$

Question 14: $A, B$ and $C$ are three points on a circle, then the perpendicular bisector of $A B, B C$ and $C A$ are________.

Solution. Given:

$A, B$ and $C$ are three points on a circle

Let $A B C$ be a triangle.

We know, a circumcentre is the point of intersection of the perpendicular bisectors of the triangle.

Thus, the perpendicular bisector of $A B, B C$ and $C A$ intersect at a point known as circumcentre.

Hence, the perpendicular bisector of $A B, B C$ and $C A$ are concurrent.

Question 15: Fill In The Blanks

If $A B$ and $A C$ are equal chords of a circle, then the biesector of $\angle B A C$ passes through the____________.

Solution. Given:

$A B$ and $A C$ are equal chords of a circle

Let $O$ be the centre of the circle.

In $\Delta O A B$ and $\Delta O A C$

$A B=A C$ (given)

$O A=O A($ common $)$

$O B=O C$ (radius of the circle)

By SSS property,

$\triangle O A B \cong \Delta O A C$

Therefore, $\angle O A B=\angle O A C$ (by C.P.C.T.)

Thus, $\angle B A C=2 \angle O A B$.

Hence, the bisector of $\angle B A C$ passes through the centre

Question 16: Fill In The Blanks

$A B C D$ is such a quadrilateral that $A$ is the centre of the circle passing through $B, C$ and $D$. If $\angle C B D$ $+\angle C D B=k \angle B A D$, then $k=$____________.

Solution. Given:

$A B C D$ is such a quadrilateral such that $A$ is the centre of the circle passing through $B, C$ and $D$ $\angle C B D+\angle C D B=k \angle B A D$

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle C A D=2 \angle C B D\ldots(1)$

Also, $\angle C A B=2 \angle C D B\ldots(2)$



Adding (1) and (2), we get

$\angle C A D+\angle C A B=2 \angle C B D+2 \angle C D B$

$\Rightarrow \angle B A D=2 \angle C B D+2 \angle C D B$

$\Rightarrow \angle B A D=2(\angle C B D+\angle C D B)$

$\Rightarrow \angle C B D+\angle C D B=\frac{1}{2} \angle B A D$

Hence, $k=\frac{1}{2} .$

Question 17: Fill In The Blanks

Two chords $A B$ and $A C$ of a circle are on the opposite sides of the centre. If $A B$ and $A C$ subtend angles equal to $90^{\circ}$ and $150^{\circ}$ respectively at the centre, then $\angle B A C=$____________.

Solution. Given:

$A B$ and $A C$ subtend angles equal to $90^{\circ}$ and $150^{\circ}$ respectively at the centre

i.e., $\angle A O B=90^{\circ}$ and $\angle A O C=150^{\circ}\ldots(1)$

In $\Delta A O B$

$O A=O B$ (radius)

$\therefore \angle O B A=\angle O A B$ (angles opposite to equal sides are equal) $\ldots(2)$

Now, $\angle O B A+\angle O A B+\angle A O B=180^{\circ}$ (angle sum property)

$\Rightarrow 2 \angle O A B+90^{\circ}=180^{\circ} \quad($ From $(1)$ and $(2))$

$\Rightarrow 2 \angle O A B=180^{\circ}-90^{\circ}$

$\Rightarrow 2 \angle O A B=90^{\circ}$

$\Rightarrow \angle O A B=45^{\circ}\ldots(3)$

In $\Delta A O C$

$O A=O C$ (radius)

$\therefore \angle O C A=\angle O A C$ (angles opposite to equal sides are equal) $\ldots(4)$

Now, $\angle O C A+\angle O A C+\angle A O C=180^{\circ}$ (angle sum property)

$\Rightarrow 2 \angle O A C+150^{\circ}=180^{\circ}$

(From (1) and (4))

$\Rightarrow 2 \angle O A C=180^{\circ}-150^{\circ}$

$\Rightarrow 2 \angle O A C=30^{\circ}$

$\Rightarrow \angle O A C=15^{\circ}\ldots(5)$

Thus,

$\angle B A C=\angle O A C+\angle O A B$

$\Rightarrow \angle B A C=15^{\circ}+45^{\circ}$

(From (3) and (5))

Hence, $\angle B A C=\underline{60}^{\circ}$.

Question 18: Fill In The Blanks

Two congruent circles have centres at $\mathrm{O}$ and $O^{\prime}$. Arc $A X b$ of circle centred at $O$, subtends an angle of $75^{\circ}$ at the centre $O$ and arc $P Y Q$ ( or circle centred at $\left.O^{\prime}\right)$ subtends an angle $25^{\circ}$ at the centre $O^{\prime}$. The ratio of the $\operatorname{arcs} A X B$ and $P Y Q$ is__________.

Solution. Given:

$\mathrm{O}$ and $\mathrm{O}^{\prime}$ are the centres of two congruent circles

$A X B$ of circle centred at $O$, subtends an angle of $75^{\circ}$ at the centre $O$

arc $P Y Q$ of circle centred at $O^{\prime}$,subtends an angle $25^{\circ}$ at the centre $O^{\prime}$

Since, the circles are congruent

Therefore, they have same radius of measure $r \mathrm{~cm}$.$\ldots(1)$

We know, Length of $\operatorname{arc}=\frac{\theta}{360^{\circ}} \times 2 \pi r$

Thus,

Length of arc $A X B=\frac{75^{\circ}}{360^{\circ}} \times 2 \pi r \quad .$ $\ldots(2)$

Length of arc $P Y Q=\frac{25^{\circ}}{360^{\circ}} \times 2 \pi r \quad \ldots$(3)

$\frac{\text { Length of } \operatorname{arc} A X B}{\text { Length of } \operatorname{arc} P Y Q}=\frac{\frac{75^{\circ}}{360^{\circ}} \times 2 \pi r}{\frac{25^{\circ}}{360^{\circ}} \times 2 \pi r}$

$=\frac{75^{\circ}}{25^{\circ}}$

$=\frac{3}{1}$

Hence, the ratio of the $\operatorname{arcs} A X B$ and $P Y Q$ is $3: 1 .$

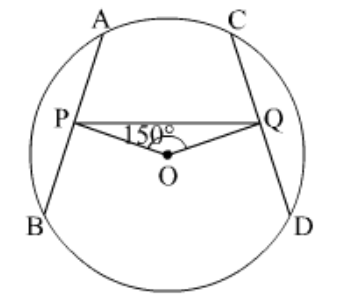
Question 19: In the given figure, $A B$ and $C D$ are two equal chords of a circle with centre O. OP and $O Q$ are perpendicular on chords $A B$ and $C D$, respectively. If $\angle P O Q=150^{\circ}$, then $\angle A P Q=$____________.



Solution. Given:

$A B=C D$

$O P \perp A B$ and $O Q \perp C D$

$\angle P O Q=150^{\circ}\ldots(1)$

In $\triangle P O Q$

$O P=O Q$ (equal chords are equidistant from the centre)

$\therefore \angle O P Q=\angle O Q P($ angles opposite to equal sides are equal) $\ldots(2)$

Now, $\angle O P Q+\angle O Q P+\angle P O Q=180^{\circ}$ (angle sum property)

$\Rightarrow 2 \angle O P Q+150^{\circ}=180^{\circ}$

(From (1) and (2))

$\Rightarrow 2 \angle O P Q=180^{\circ}-150^{\circ}$

$\Rightarrow 2 \angle O P Q=30^{\circ}$

$\Rightarrow \angle O P Q=15^{\circ}\ldots(3)$

Since, $O P \perp A B$

Thus, $\angle O P A=90^{\circ}\ldots(4)$

Now, $\angle O P A=\angle O P Q+\angle A P Q$

$\Rightarrow 90^{\circ}=15^{\circ}+\angle A P Q$

$($ From $(3)$ and $(4))$

$\Rightarrow \angle A P Q=90^{\circ}-15^{\circ}$

$\Rightarrow \angle A P Q=75^{\circ}$

Hence, $\angle A P Q=\underline{75}^{\circ}$.

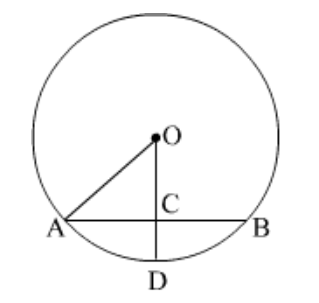
Question 20: In the given figure, if $O A=5 \mathrm{~cm}, A B=8 \mathrm{~cm}$ and $O D$ is perpendicular to $A B$, then $C D$ is equal to____________.



Solution. Given:

$O A=5 \mathrm{~cm}\ldots(1)$

$A B=8 \mathrm{~cm}$

$O D$ is perpendicular to $A B$

We know, perpendicular from the centre to the chord bisects the chord.

Therefore, $A C=C B=\frac{1}{2} A B$

$\Rightarrow A C=4 \mathrm{~cm}\ldots(2)$

In right angled $\Delta O A C$,

Using pythagoras theorem

$O A^{2}=A C^{2}+O C^{2}$

$\Rightarrow 5^{2}=4^{2}+O C^{2} \quad($ From $(1)$ and $(2))$

$\Rightarrow 25=16+O C^{2}$

$\Rightarrow O C^{2}=25-16$

$\Rightarrow O C^{2}=9$

$\Rightarrow O C=3 \mathrm{~cm}$

$O D=5 \mathrm{~cm}$ (radius)

$\therefore C D=O D-O C$

$\Rightarrow C D=5-3$

$\Rightarrow C D=2 \mathrm{~cm}$

Hence, $C D$ is equal to $2 \mathrm{~cm}$.

Question 21: In the given figure, if $\angle \mathrm{ABC}=20$ o , then $\angle \mathrm{AOC}$ is equal to______.



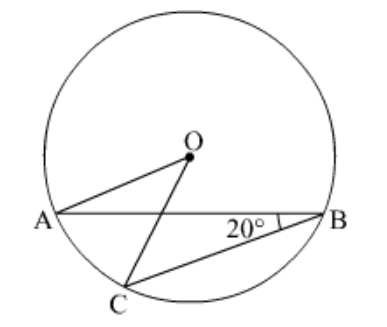
Solution. Given:

$\angle A B C=20^{\circ}\ldots(1)$

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle A O C=2 \angle A B C$

$\Rightarrow \angle A O C=2\left(20^{\circ}\right) \quad$ (From (1))

$\Rightarrow \angle A O C=40^{\circ}$

Hence, $\angle A O C$ is equal to $\underline{40}^{\circ}$.

Question 22: In the given figure, if $A O B$ is a diameter of the circle and $A C=B C$, then $\angle C A B$ is equal to________.



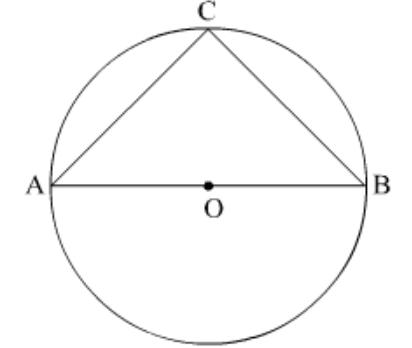
Solution. Given:

$A O B$ is a diameter of the circle

$A C=B C$

We know, the diameter subtends a right angle to any point on the circle.

$\therefore \angle A C B=90^{\circ}\ldots(1)$

In $\Delta A C B$

$A C=B C$ (given)

$\therefore \angle C A B=\angle C B A$ (angles opposite to equal sides are equal) $\ldots(2)$

Now,

$\angle C A B+\angle C B A+\angle A C B=180^{\circ}$ (angle sum property)

$\Rightarrow 2 \angle C A B+90^{\circ}=180^{\circ} \quad$ (From (1) and (2))

$\Rightarrow 2 \angle C A B=180^{\circ}-90^{\circ}$

$\Rightarrow 2 \angle C A B=90^{\circ}$

$\Rightarrow \angle C A B=45^{\circ}$

Hence, $\angle C A B$ is equal to $\underline{45}^{\circ}$

Question 23: In the given figure, $\angle A O B=90^{\circ}$ and $\angle A B C=30^{\circ}$, then $\angle C A O$ is equal to_________.



Solution. Given:

$\angle A O B=90^{\circ}\ldots(1)$

$\angle A B C=30^{\circ}\ldots(2)$

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle A O B=2 \angle A C B$

$\Rightarrow 90^{\circ}=2 \angle A C B$

$\Rightarrow \angle A C B=45^{\circ}\ldots(3)$

In $\Delta A C B$

$\angle C A B+\angle C B A+\angle A C B=180^{\circ}$ (angle sum property)

$\Rightarrow \angle C A B+30^{\circ}+45^{\circ}=180^{\circ} \quad($ From $(2)$ and $(3))$

$\Rightarrow \angle C A B+75^{\circ}=180^{\circ}$

$\Rightarrow \angle C A B=180^{\circ}-75^{\circ}$

$\Rightarrow \angle C A B=105^{\circ}\ldots(4)$

Also, in $\Delta O A B$,

$O A=O B$

$\therefore \angle O A B=\angle O B A$ (angles opposite to equal sides are equal) $\ldots(5)$

Now,

$\angle O A B+\angle O B A+\angle A O B=180^{\circ}$ (angle sum property)

$\Rightarrow 2 \angle O A B+90^{\circ}=180^{\circ} \quad($ From $(1)$ and $(5))$

$\Rightarrow 2 \angle O A B=180^{\circ}-90^{\circ}$

$\Rightarrow 2 \angle O A B=90^{\circ}$

$\Rightarrow \angle O A B=45^{\circ}\ldots(6)$

$\angle C A O=\angle C A B-\angle O A B$

$=105^{\circ}-45^{\circ}$ (From (4) and (6))

$=60^{\circ}$

Hence, $\angle C A O$ is equal to $\underline{60}^{\circ}$

Question 24: In the given figure, if $\angle O A B=40$ o , then $\angle A C B=$_________.



Solution. Given:

$\angle O A B=40^{\circ}\ldots(1)$

In $\Delta O A B$

$O A=O B$

$\therefore \angle O A B=\angle O B A=40^{\circ}$ (angles opposite to equal sides are equal) $\ldots(2)$

Now,

$\angle O A B+\angle O B A+\angle A O B=180^{\circ}$ (angle sum property)

$\Rightarrow 40^{\circ}+40^{\circ}+\angle A O B=180^{\circ} \quad$ (From (1) and (2))

$\Rightarrow \angle A O B=180^{\circ}-80^{\circ}$

$\Rightarrow \angle A O B=100^{\circ}$.

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle A O B=2 \angle A C B$

$\Rightarrow 100^{\circ}=2 \angle A C B \quad($ From $(3))$

$\Rightarrow \angle A C B=50^{\circ}$

Hence, $\angle A C B=\underline{50}^{\circ} .$

Question 25: In the given figure,, if $\angle D A B=60 \circ, \angle A B D=50 \circ$, then $\angle A C B=$______.



Solution. Given:

$\angle D A B=60^{\circ}\ldots(1)$

$\angle A B D=50^{\circ}\ldots(2)$

In $\Delta A D B$

$\angle D A B+\angle D B A+\angle A D B=180^{\circ}$ (angle sum property)

$\Rightarrow 60^{\circ}+50^{\circ}+\angle A D B=180^{\circ} \quad$ (From (1) and (2))

$\Rightarrow \angle A D B=180^{\circ}-110^{\circ}$

$\Rightarrow \angle A D B=70^{\circ} \quad \ldots$

We know, angles in the same segment of the circle are equal.

Thus, $\angle A D B=\angle A C B$

$\Rightarrow 70^{\circ}=\angle A C B \quad($ From $(3))$

$\Rightarrow \angle A C B=70^{\circ}$

Hence, $\angle A C B=\underline{70^{\circ}}$.

Question 26: In the given figure, $\mathrm{BC}$ is a diameter of circle and $\angle \mathrm{BAO}=60 \mathrm{o}$. Then, $\angle \mathrm{ADC}=$___________.



Solution. Given:

$B C$ is a diameter of circle

$\angle B A O=60^{\circ}\ldots(1)$

In $\triangle O A B$

$O A=O B$

$\therefore \angle O A B=\angle O B A=60^{\circ}$ (angles opposite to equal sides are equal) $\ldots(2)$

Also,

$\angle A O C=\angle O A B+\angle O B A$ (exterior angle)

$\Rightarrow \angle A O C=60^{\circ}+60^{\circ}(\mathrm{From}(2))$

$\Rightarrow \angle A O C=120^{\circ}\ldots(3)$

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle A O C=2 \angle A D C$

$\Rightarrow 120^{\circ}=2 \angle A D C \quad($ From $(3))$

$\Rightarrow \angle A D C=60^{\circ}$

Hence, $\angle A D C=\underline{60}^{\circ}$.

Question 27: In the given figure, if $A O B$ is a diameter and $\angle A D C=120^{\circ}$, then $\angle C A B=$__________.



Solution. Given:

$A O B$ is a diameter of circle

$\angle A D C=120^{\circ}$

Quadrilateral $A D C B$ is a cyclic quadrilateral.

In a cyclic quadrilateral, the sum of opposite angles is $180^{\circ}$.

Thus, $\angle A D C+\angle C B A=180^{\circ}$

$\Rightarrow 120^{\circ}+\angle C B A=180^{\circ}$

$\Rightarrow \angle C B A=180^{\circ}-120^{\circ}$

$\Rightarrow \angle C B A=60^{\circ}\ldots(1)$

We know, the diameter subtends a right angle to any point on the circle.

$\therefore \angle A C B=90^{\circ}\ldots(2)$

In $\Delta A C B$

$\angle C A B+\angle C B A+\angle A C B=180^{\circ}$ (angle sum property)



$\Rightarrow \angle C A B+60^{\circ}+90^{\circ}=180^{\circ} \quad($ From $(1)$ and $(2))$

$\Rightarrow \angle C A B=180^{\circ}-150^{\circ}$

$\Rightarrow \angle C A B=30^{\circ}$-..(3)

Hence, $\angle C A B=\underline{30}^{\circ}$

Question 28: In the given figure, if $A O C$ is a diameter of the circle and $A X B=\frac{1}{2}$ are $B Y C$, then $\angle B O C=$_____________.



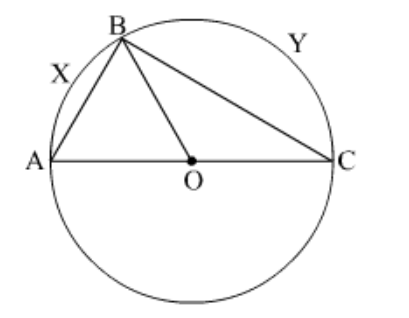
Solution. Given:

$A O C$ is a diameter of circle

$\operatorname{arc} A X B=\frac{1}{2} \operatorname{arc} B Y C$

$\Rightarrow \angle B O A=\frac{1}{2} \angle B O C$..(1)

Now, $\angle B O A+\angle B O C=180^{\circ}$

(Angles on a straight line)

$\Rightarrow \frac{1}{2} \angle B O C+\angle B O C=180^{\circ}$(From (1))

$\Rightarrow \frac{3}{2} \angle B O C=180^{\circ}$

$\Rightarrow \angle B O C=\frac{2}{3} \times 180^{\circ}$

$\Rightarrow \angle B O C=120^{\circ}$

Hence, $\angle B O C=120^{\circ}$

Question 29: In the given figure, $\angle A B C=45^{\circ}$, then $\angle A O C=$___________.



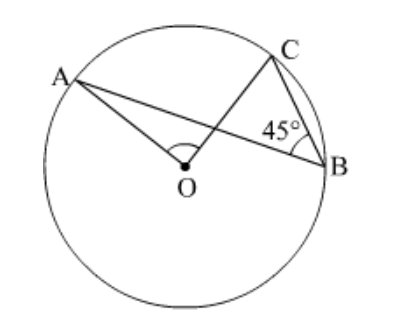
Solution. Given:

$\angle A B C=45^{\circ}$. .(1)

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle A O C=2 \angle A B C$

$\Rightarrow \angle A O C=2\left(45^{\circ}\right)$

$\Rightarrow \angle A O C=90^{\circ}$

Hence, $\angle A O C=\underline{90}^{\circ}$.

Question 30: In the given figure, if $\angle A D C=130^{\circ}$ and chord $B C=$ chord $B E$, then $\angle C B E=$_________.



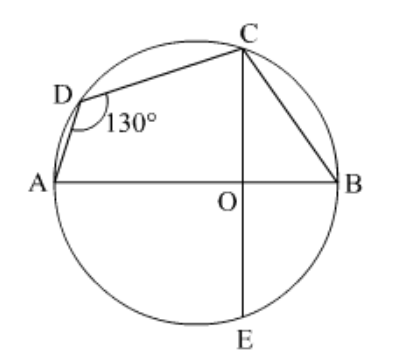
Solution. Given:

$\angle A D C=130^{\circ}\ldots(1)$

chord $B C=$ chord $B E \cdots(2)$

Quadrilateral $A D C B$ is a cyclic quadrilateral.

In a cyclic quadrilateral, the sum of opposite angles is $180^{\circ}$

Thus, $\angle A D C+\angle C B A=180^{\circ}$

$\Rightarrow 130^{\circ}+\angle C B A=180^{\circ}$

$\Rightarrow \angle C B A=180^{\circ}-130^{\circ}$

$\Rightarrow \angle C B A=50^{\circ}\ldots(3)$

In $\triangle C B O$ and $\triangle E B O$,

$B C=B E$ (given)

$O B=O B($ common $)$

$O C=O E$ (radius of the circle)

By SSS property,

$\Delta O C B \cong \Delta O E B$

Therefore, $\angle O B C=\angle O B E=50^{\circ}$ (by C.P.C.T.) $\ldots(4)$

Thus, $\angle C B E=\angle O B E+\angle O B C$

$=50^{\circ}+50^{\circ} \quad$ (From $\left.(4)\right)$

$=100^{\circ}$

Hence, $\angle C B E=100^{\circ}$.

Question 31: In the given figure, if $\angle A C B=40^{\circ}$, then $\angle A O B=$ and $\angle O A B=$_________.



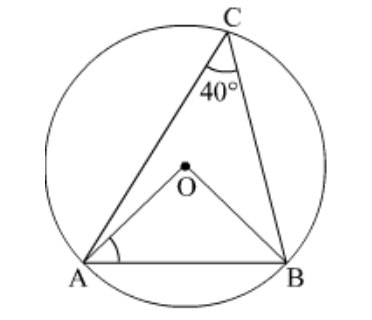
Solution. Given:

$\angle A C B=40^{\circ}\ldots(1)$

We know, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.

Thus, $\angle A O B=2 \angle A C B$

$\Rightarrow \angle A O B=2\left(40^{\circ}\right)$ (From (1))

$\Rightarrow \angle A O B=80^{\circ}\ldots(2)$

In $\triangle A O B$

$O A=O B$ (radius)

$\therefore \angle O A B=\angle O B A$ (angles opposite to equal sides are equal) $\ldots(3)$

$\angle O A B+\angle O B A+\angle A O B=180^{\circ}$ (angle sum property)

$\Rightarrow 2 \angle O A B+80^{\circ}=180^{\circ}$

(From (2) and (3))

$\Rightarrow 2 \angle O A B=180^{\circ}-80^{\circ}$

$\Rightarrow 2 \angle O A B=100^{\circ}$

$\Rightarrow \angle O A B=50^{\circ}$

Hence, $\angle A O B=\underline{80}^{\circ}$ and $\angle O A B=\underline{50}^{\circ}$

Question 32: In the given figure, $A O B$ is a diameter of the circle and $C, D, E$ are any three points to semi circle then $\angle A C D+\angle B E D=$__________.



Solution. Given:

$A O B$ is a diameter of the circle

We know, the diameter subtends a right angle to any point on the circle.

$\therefore \angle A E B=90^{\circ}\ldots(1)$

Quadrilateral $A C D E$ is a cyclic quadrilateral.

In a cyclic quadrilateral, the sum of opposite angles is $180^{\circ}$.

Thus, $\angle A C D+\angle D E A=180^{\circ}\ldots(2)$

Adding (1) and (2), we get

$\angle A C D+\angle D E A+\angle A E B=90^{\circ}+180^{\circ}$

$\Rightarrow \angle A C D+\angle D E B=270^{\circ}$

Hence, $\angle A C D+\angle B E D=270^{\circ}$.

Question 33: In the given figure, if $\angle O A B=30^{\circ}$ and $\angle O C B=57^{\circ}$, then $\angle B O C=$________ and $\angle A O C=$__________



Solution. Given:

$\angle O A B=30^{\circ}\ldots(1)$

$\angle O C B=57^{\circ}\ldots(2)$

In $\Delta C O B$

$O C=O B$ (radius)

$\therefore \angle O C B=\angle O B C=57^{\circ}$ (angles opposite to equal sides are equal) $\ldots(3)$

$\angle O C B+\angle O B C+\angle C O B=180^{\circ}$

(angle sum property)

$\Rightarrow 57^{\circ}+57^{\circ}+\angle C O B=180^{\circ}$

$($ From $(3))$

$\Rightarrow \angle C O B=180^{\circ}-114^{\circ}$

$\Rightarrow \angle C O B=66^{\circ}\ldots(4)$

In $\triangle A O B$

$O A=O B$ (radius)

$\therefore \angle O A B=\angle O B A=30^{\circ}$ (angles opposite to equal sides are equal) $\ldots(5)$

$\angle O A B+\angle O B A+\angle A O B=180^{\circ}$ (angle sum property)

$\Rightarrow 30^{\circ}+30^{\circ}+\angle A O B=180^{\circ}$(From (5))

$\Rightarrow \angle A O B=180^{\circ}-60^{\circ}$

$\Rightarrow \angle A O B=120^{\circ}\ldots(6)$

Now,

$\angle A O B=\angle A O C+\angle C O B$

$\Rightarrow 120^{\circ}=\angle A O C+66^{\circ}$ $\Rightarrow / A O C=120^{\circ}-66^{\circ}$

(From (4) and (6))

$\Rightarrow \angle A O C=120^{\circ}-66^{\circ}$

$\Rightarrow \angle A O C=54^{\circ}$

Hence, $\angle B O C=\underline{66^{\circ}}$ and $\angle A O C=\underline{54}^{\circ}$.

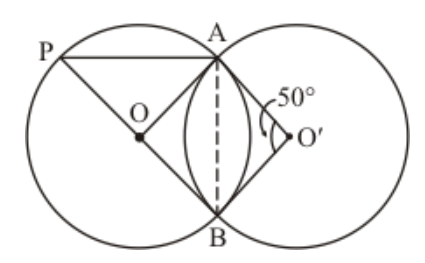
Question 1: In the given figure, two circles intersect at $A$ and $B$. The centre of the smaller circle is $O$ and it lies on the circumference of the larger circle. If $\angle A P B=70^{\circ}$, find $\angle A C B$.



Solution. Consider the smaller circle whose centre is given as ' $O$ '.

The angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.

So, here we have

$\angle A O B=2 / A P $

$=2\left(70^{\circ}\right)$

$\angle A O B=140^{\circ}$

Now consider the larger circle and the points ' $A^{\prime},{ }^{\prime} C^{\prime},{ }^{‘} B^{\prime}$ and ' $O$ ' along its circumference. ' $A C B O$ ' form a cyclic quadrilateral.

In a cyclic quadrilateral it is known that the opposite angles are supplementary, meaning that the opposite angles add up to $180^{\circ}$.

$\angle A O B+\angle A C B=180^{\circ}$

$\angle A C B=180^{\circ}-\angle A O B$

$=180^{\circ}-140^{\circ}$

$\angle A C B=40^{\circ}$

Hence , the measure of $\angle A C B$ is $40^{\circ}$.

Question 2: In the given figure, two congruent circles with centres $O$ and $O$ ' intersect at $A$ and $B$. If $\angle A O B=50^{\circ}$, then find $\angle A P B$.



Solution. Since both the circles are congruent, they will have equal radii. Let their radii be ' $r$ '.

So, from the given figure we have,

$O A=O B=O^{\prime} A=O^{\prime} B=r$



Now, since all the sides of the quadrilateral $O B O^{\prime} A$ are equal it has to be a rhombus.

One of the properties of a rhombus is that the opposite angles are equal to each other.

So, since it is given that $\angle A O^{\prime} B=50^{\circ}$, we can say that the angle opposite it, that is to say that $\angle A O B$ should also have the same value.

Hence we get $\angle A O B=50^{\circ}$

Now, consider the first circle with the centre ' $O$ ' alone. ' $A B$ ' forms a chord and it subtends an angle of $50^{\circ}$ with its centre, that is $\angle A O B=50^{\circ}$.

A property of a circle is that the angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.

This means that,

$\angle A P B=\frac{\angle A O B}{2}$

$=\frac{50^{\circ}}{2}$

$=25^{\circ}$

Hence the measure of $\angle A P B$ is $25^{\circ}$

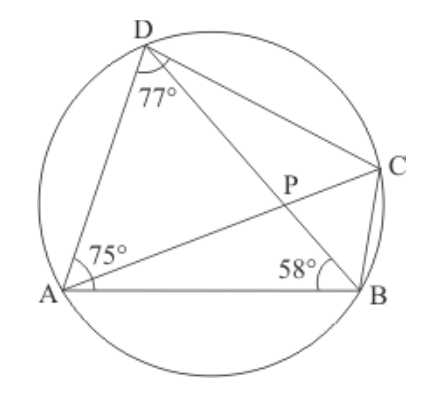
Question 3: In the given figure, $A B C D$ is a cyclic quadrilateral in which $\angle B A D=75^{\circ}, \angle A B D=58^{\circ}$ and $\angle A D C=$ $77^{\circ}, A C$ and $B D$ intersect at $P$. Then, find $\angle D P C$.



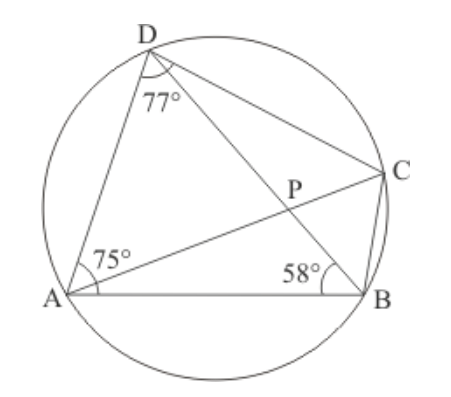
Solution. In a cyclic quadrilateral it is known that the opposite angles are supplementary, meaning that the opposite angles add up to $180^{\circ}$.

Here we have a cyclic quadrilateral $A B C D$. The centre of this circle is given as ' $O$ '.



Since in a cyclic quadrilateral the opposite angles are supplementary, here

$\angle C B D=180^{\circ}-\angle A D C-\angle A B D$



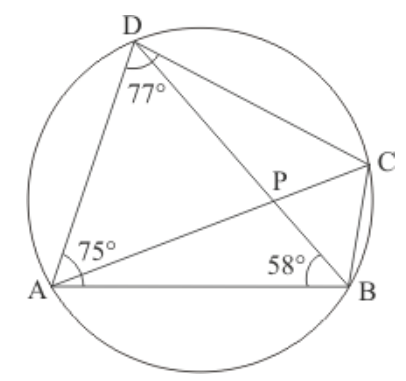
Solution. In a cyclic quadrilateral it is known that the opposite angles are supplementary, meaning that the opposite angles add up to $180^{\circ}$.

Here we have a cyclic quadrilateral $A B C D$. The centre of this circle is given as ' $O$ '.



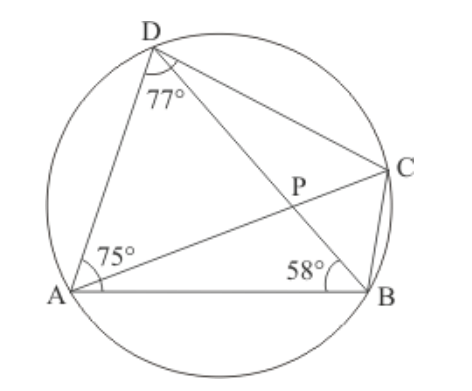
Since in a cyclic quadrilateral the opposite angles are supplementary, here

$\angle A D C+\angle A B D+\angle C B D=180^{\circ}$

$\angle C B D=180^{\circ}-\angle A D C-\angle A B D$

$=180^{\circ}-77^{\circ}-58^{\circ}$

$\angle C B D=45^{\circ}$

Whenever a chord is drawn in a circle two segments are formed. One is called the minor segment while the other is called the major segment. The angle that the chord forms with any point on the circumference of a particular segment is always the same.

Here, ' $C D$ ' is a chord and ' $A$ ' and ' $B$ ' are two points along the circumference on the major segment formed by the chord ' $C D$ '.

So, $\angle C B D=\angle C A D=45^{\circ}$

Now,

$\angle B A D=\angle B A C+\angle C A D$

\begin{aligned}

\angle B A C &=\angle B A D-\angle C A D \\

&=75^{\circ}-45^{\circ}

$\angle B A C=30^{\circ}$

In any triangle the sum of the interior angles need to be equal to $180^{\circ}$.

Consider the triangle $\triangle A B P$,

$\angle P A B+\angle A B P+\angle A P B=180^{\circ}$

$\Rightarrow \angle A P B=180^{\circ}-30^{\circ}-58^{\circ}$

$\Rightarrow \angle A P B=92^{\circ}$

From the figure, since ' $A C^{\prime}$ and ' $B D$ ' intersect at ' $P$ ' we have,

$\angle A P B=\angle D P C=92^{\circ}$

Hence the measure of $\angle D P C$ is $92^{\circ}$.

Question 4: In the given figure, if $\angle A O B=80^{\circ}$ and $\angle A B C=30^{\circ}$, then find $\angle C A O$.



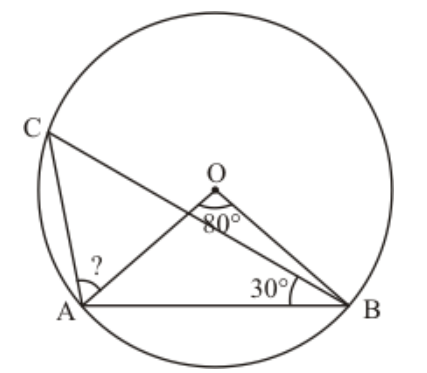
Solution. Consider the given circle with the centre ' $O$ '. Let the radius of this circle be ' $r$ ' $. A B$ ' forms a chord and it subtends an angle of $80^{\circ}$ with its centre, that is $\angle A O B=80^{\circ}$.

The angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.



So, here we have

$\angle A C B=\frac{\angle A O B}{2}$

$=\frac{80^{\circ}}{2}$

$\angle A C B=40^{\circ}$

In any triangle the sum of the interior angles need to be equal to $180^{\circ}$.

Consider the triangle $\triangle A O B$

$\angle A O B+\angle O A B+\angle O B A=180^{\circ}$

Since, $O A=O B=r$, we have $\angle O A B=\angle O B A$. So the above equation now changes to

$\angle A O B+\angle O A B+\angle O A B=180^{\circ}$

$2 \angle O A B=180^{\circ}-\angle A O B$

$=180^{\circ}-80^{\circ}$

$2 \angle O A B=100^{\circ}$

$\angle O A B=50^{\circ}$

Considering the triangle $\triangle A B C$ now,

$\angle A C B+\angle O A B+\angle O A C+\angle A B C=180^{\circ}$

$\angle O A C=180^{\circ}-\angle A C B-\angle O A B-\angle A B C$

$=180^{\circ}-40^{\circ}-50^{\circ}-30^{\circ}$

$\angle O A C=60^{\circ}$

Hence, the measure of $\angle C A O$ is $60^{\circ}$.

Question 5: In the given figure, $A$ is the centre of the circle. $A B C D$ is a parallelogram and $C D E$ is a straight line. Find $\angle B C D: \angle A B E$



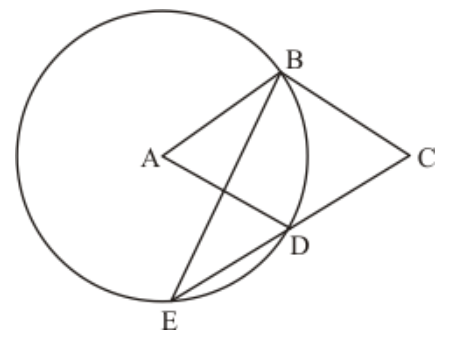
Solution. It is given that ' $A B C D$ ' is a parallelogram. But since ' $A$ ' is the centre of the circle, the lengths of ' $A B$ ' and ' $A D$ ' will both be equal to the radius of the circle.



So, we have $A B=A D$.

Whenever a parallelogram has two adjacent sides equal then it is a rhombus.

So ' $A B C D$ ' is a rhombus.

Let $\angle B D E=x^{\circ}$.

We know that in a circle the angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.

By this property we have

$\angle B A D=2(\angle B D E)$

$\angle B A D=2 x^{\circ}$

In a rhombus the opposite angles are always equal to each other.

So, $\angle B A D=\angle B C E=2 x^{\circ}$

Since the sum of all the internal angles in any triangle sums up to $180^{\circ}$ in triangle $\Delta B E C$, we have

$\angle B E C+\angle B C E+\angle E B C=180^{\circ}$

$\angle E B C=180^{\circ}-\angle B E C-\angle B C E$

$=180^{\circ}-x^{\circ}-2 x^{\circ}$

$\angle E B C=180^{\circ}-3 x^{\circ}$

In the rhombus ' $A B C D$ ' since one pair of opposite angles are ' $2 x^{\circ}$ ' the other pair of opposite angles have to be $\left(180^{\circ}-2 x^{\circ}\right)$

From the figure we see that,

$\angle E B C+\angle A B E=\angle A B C$

$\angle A B E=\angle A B C-\angle E B C$

$=180^{\circ}-2 x^{\circ}-\left(180^{\circ}-3 x^{\circ}\right)$

$\angle A B E=x^{\circ}$

So now we can write the required ratio as,

$\frac{\angle B C D}{\angle A B E}=\frac{2 x^{\circ}}{x^{\circ}}$

$\frac{\angle B C D}{\angle A B E}=\frac{2}{1}$

Hence the ratio between the given two angles is $2: 1$.

Question 6: In the given figure, $A B$ is a diameter of the circle such that $\angle A=35^{\circ}$ and $\angle Q=25^{\circ}$, find $\angle P B R$.



Solution. Let us first consider the triangle $\triangle A B Q$.



It is known that in a triangle the sum of all the interior angles add up to $180^{\circ}$.

So here in our triangle $\triangle A B Q$ we have,

$\angle B A Q+\angle A Q B+\angle A B Q=180^{\circ}$

$\angle A B Q=180^{\circ}-\angle B A Q-\angle A Q B$

$=180^{\circ}-35^{\circ}-25^{\circ}$

$\angle A B Q=120^{\circ}$

By a property of the circle we know that an angle formed in a semi-circle will be $90^{\circ} .$

In the given circle since ' $A B$ ' is the diameter of the circle the angle $\angle A P B$ which is formed in a semicircle will have to be $90^{\circ}$.

So, we have $\angle A P B=90^{\circ}$

Now considering the triangle $\triangle A P B$ we have,

$\angle A P B+\angle B A P+\angle A B P=180^{\circ}$

$\angle A B P=180^{\circ}-\angle A P B-\angle B A P$

$=180^{\circ}-90^{\circ}-35^{\circ}$

$\angle A B P=55^{\circ}$

From the given figure it can be seen that,

$\angle A B P+\angle P B Q=\angle A B Q$

$\angle P B Q=\angle A B Q-\angle A B P$

$=120^{\circ}-55^{\circ}$

$\angle P B Q=65^{\circ}$

Now, we can also say that,

$\angle P B Q+\angle P B R=180^{\circ}$

$\angle P B R=180^{\circ}-\angle P B Q$

$=180^{\circ}-65^{\circ}$

$\angle P B R=115^{\circ}$

Hence the measure of the angle $\angle P B R$ is $115^{\circ}$

Question 7: In the given figure, $P$ and $Q$ are centres of two circles intersecting at $B$ and $C . A C D$ is a straight line. Then, $\angle B Q D=$



Solution. Consider the circle with the centre ' $P$ '.

The angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.



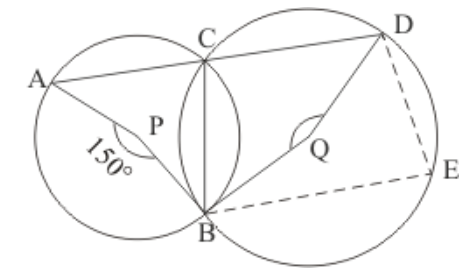
So, here we have

$\angle A C B=\frac{\angle A P B}{2}$

$=\frac{150^{\circ}}{2}$

$\angle A C B=75^{\circ}$

Since ' $A C D$ ' is a straight line, we have

$\angle A C B+\angle B C D=180^{\circ}$

$\angle B C D=180^{\circ}-\angle A C B$

$=180^{\circ}-75^{\circ}$

$\angle B C D=105^{\circ}$

Now let us consider the circle with centre ' $Q$ '. Here let ' $E$ ' be any point on the circumference along the major arc ' $B D^{\prime}$. Now ' $C B E D$ ' forms a cyclic quadrilateral.

In a cyclic quadrilateral it is known that the opposite angles are supplementary, meaning that the opposite angles add up to $180^{\circ}$.

So here,

$\angle B C D+\angle B E D=180^{\circ}$

$\angle B E D=180^{\circ}-\angle B C D$

$=180^{\circ}-105^{\circ}$

$\angle B E D=75^{\circ}$

The angle subtended by an arc at the centre of the circle is double the angle subtended by the arc in the remaining part of the circle.

So, now we have

$\angle B Q D=2 \angle B E D$ $=2\left(75^{\circ}\right)$



$\angle B Q D=150^{\circ}$

Hence, the measure of $\angle B Q D$ is $150^{\circ}$. Question 8: In the given figure, if $O$ is the circumcentre of $\angle A B C$, then find the value of $\angle O B C+\angle B A C$.



Solution.



Since, $\mathrm{O}$ is the circumcentre of $\triangle A B C$, So, O would be centre of the circle passing through points $A, B$ and $C$.

$\angle A B C=90^{\circ}$

(Angle in the semicircle is $90^{\circ}$.)

$\Rightarrow \angle O A B+\angle O B C=90^{\circ}\ldots (1)$

As $O A=O B \quad$ (Radii of the same circle)

$\therefore \angle O A B=\angle O B A \quad$ (Angle opposite to equal sides are equal)

or, $\angle B A C=\angle O B A$

From (1)

$\angle B A C+\angle O B C=90^{\circ}$

Question 9: If the given figure, $A O C$ is a diameter of the circle and $\operatorname{arc} A \times B=\frac{1}{2}$ arc $B Y C$. Find $\angle B O C$.



Solution. We need to find $\angle B O C$



$\operatorname{arc} A X B=\frac{1}{2} \operatorname{arc} B Y C$

$\angle A O B=\frac{1}{2} \angle B O C$

Also $\angle A O B+\angle B O C=180^{\circ}$

Therefore, $\frac{1}{2} \angle B O C+\angle B O C=180^{\circ}$

$\Rightarrow \angle B O C=\frac{2}{3} \times 180^{\circ}=120^{\circ}$

Question 10: In the given figure, $A B C D$ is a quadrilateral inscribed in a circle with centre $O . C D$ is produced to $E$ such that $\angle A E D=95^{\circ}$ and $\angle O B A=30^{\circ}$. Find $\angle O A C$.



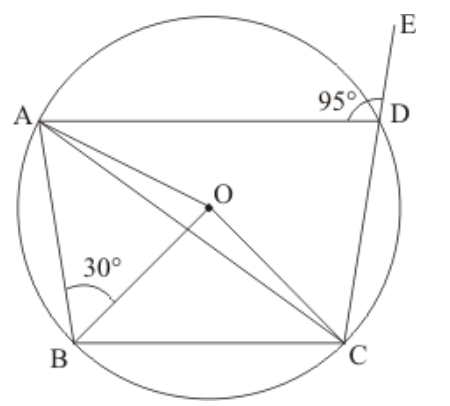
Solution. We are given $A B C D$ is a quadrilateral with center $O, \angle A D E=95^{\circ}$ and $\angle O B A=30^{\circ}$

We need to find $\angle O A C$

We are given the following figure



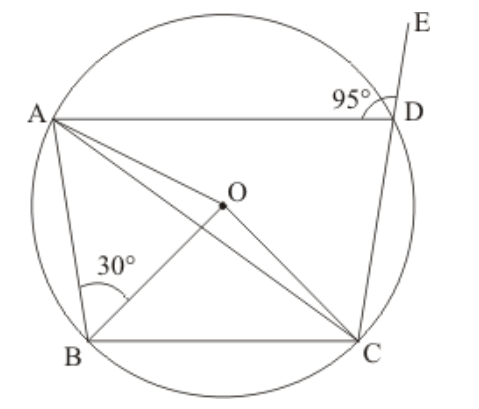
Since $\angle A D E=95^{\circ}$

$\Rightarrow \angle A D C=180^{\circ}-95^{\circ}=85^{\circ}$

Since squo; $A B C D$ is cyclic quadrilateral

This means

$\angle A B C+\angle A D C=180^{\circ}$

$\Rightarrow \quad \angle A B O+\angle O B C+\angle A D C=180^{\circ}$

$\Rightarrow \quad 30+\angle O B C+85^{\circ}=180^{\circ}$

$\Rightarrow \quad \angle O B C=180^{\circ}-115^{\circ}=65^{\circ}$

Since $O B=O C$ (radius)

$\Rightarrow \angle O B C=\angle O C B=65^{\circ}$

In $\Delta O B C$

$\angle B O C+\angle O B C+\angle O B C=180^{\circ}$

$\angle B O C+2 \angle O B C=180^{\circ}$

$\angle B O C+2 \times 65=180^{\circ}$

$\Rightarrow \quad \angle B O C=180^{\circ}-130^{\circ}$

$\Rightarrow \quad \angle B O C=50^{\circ}$

Since $Ð \mathrm{BAC}$ and $\mathrm{ĐBOC}$ are formed on the same base which is chord.

So

$\angle B A C=\frac{\angle B O C}{2}$

$=\frac{50}{2}$

$\angle B A C=25^{\circ}$

Consider $\triangle B O A$ which is isosceles triangle.

$\angle \mathrm{OAB}=30^{\circ}$

$\Rightarrow \angle O A C+\angle B A C=30^{\circ}$

$\Rightarrow \quad \angle O A C+25=30^{\circ}$

$\Rightarrow \quad \angle O A C=5^{\circ}$

Question 1: The radius of a circle is $8 \mathrm{~cm}$ and the length of one of its chords is $12 \mathrm{~cm}$. Find the distance of the chord from the centre.

Solution. Let $A B$ be a chord of a circle with centre $O$ and radius $8 \mathrm{~cm}$ such that

$A B=12 \mathrm{~cm}$

We draw $O L \perp A B$ and join $O A$.



Since, the perpendicular from the centre of a circle to a chord bisects the chord.

$A L=L B=\frac{1}{2} \times A B$

$=\frac{1}{2} \times 12$

$=6$

Now in $\triangle O A L$ we have

$O L^{2}=O A^{2}-A L^{2}$

$=8^{2}-6^{2}$

$=64-36$

$=28$

$\Rightarrow O L=\sqrt{28}=5.291$

Hence the distance of chord from the centre $5.291 \mathrm{~cm}$.

Question 2: Find the length of a chord which is at a distance of $5 \mathrm{~cm}$ from the centre of a circle of radius $10 \mathrm{~cm}$.

Solution. Given that $O A=10 \mathrm{~cm}$ and $O L=5 \mathrm{~cm}$, we have to find the length of chord $A B$.

Let $A B$ be a chord of a circle with centre $O$ and radius $10 \mathrm{~cm}$ such that $A O=10 \mathrm{~cm}$

We draw $O L \perp A B$ and join $O A$.



Since, the perpendiculars from the centre of a circle to a chord bisect the chord.

Now in $\Delta O A L$ we have

$A L^{2}=O A^{2}-O L^{2}$

$=10^{2}-5^{2}$

$=100-25$

$=75$

$\Rightarrow A L=\sqrt{75}$

$=8.66$

Hence the length of chord

$A B=2 \times A L$

$=2 \times 8.66$

$=17.32 \mathrm{~cm}$

Question 3: Find the length of a chord which is at a distance of $4 \mathrm{~cm}$ from the centre of the circle of radius $6 \mathrm{~cm}$.

Solution. Given that $O A=6 \mathrm{~cm}$ and $O L=4 \mathrm{~cm}$, find the length of chord $A B$

Let $A B$ be a chord of a circle with centre $O$ and radius $6 \mathrm{~cm}$ such that

$A O=6 \mathrm{~cm}$

We draw $O L \perp A B$ and join $O A$.



Since, the perpendicular from the centre of a circle to a chord bisects the chord.

Now in $\triangle O A L$ we have

$A L^{2}=O A^{2}-O L^{2}$

$=6^{2}-4^{2}$

$=36-16$

$=20$

$\Rightarrow A L=\sqrt{20}=4.47$

$A B=2 \times A L$

$=2 \times 4.47$

$=8.94 \mathrm{~cm}$

Hence the length of the chord is $8.94 \mathrm{~cm}$.

Question 4: Give a method to find the centre of a given circle.

Solution. Let $A, B$ and $C$ are three distinct points on a circle $C(O, r)$.

Now join $A B$ and $B C$ and draw their perpendicular bisectors.

The point of intersection of the perpendicular bisectors is the centre of given circle.

Hence $O$ is the centre of circle $C(O, r)$.



Question 5: Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.

Solution. Let $M N$ is the diameter and chord $A B$ of circle $C(O, r)$ then according to the question

$A P=B P$

Then we have to prove that $\angle A O M=\angle B O M$.

Join $O A$ and $O B$.



In $\triangle \mathrm{AOP}$ and $\triangle \mathrm{BOP}$

$O A=O B$

(Radii of the same circle)

$A P=B P \quad(P$ is the mid point of chord $A B)$

$O P=O P$(Common)

$\Rightarrow \angle A O P=\angle B O P$

(by cpct)

$\Rightarrow \angle A O M=\angle B O M$

Hence, proved.

Question 6: A line segment $A B$ is of length $5 \mathrm{~cm}$. Draw a circle of radius $4 \mathrm{~cm}$ passing through $A$ and $B$. Can you draw a circle of radius $2 \mathrm{~cm}$ passing through $A$ and $B$ ? Give reason in support of your answer.

Solution. Given that a line $A B=5 \mathrm{~cm}$, one circle having radius of $r_{1}=4 \mathrm{~cm}$ which is passing through point $A$ and $B$ and other circle of radius $r_{2}=2 \mathrm{~cm}$.

As we know that the largest chord of any circle is equal to the diameter of that circle.

So, $2 \times r_{2}A B$

There is no possibility to draw a circle whose diameter is smaller than the length of the chord.

Question 7: An equilateral triangle of side $9 \mathrm{~cm}$ is inscribed in a circle. Find the radius of the circle.

Solution. Let $A B C$ be an equilateral triangle of side $9 \mathrm{~cm}$ and let $A D$ be one of its medians. Let $G$ be the centroid of $\triangle A B C$. Then $A G: G D=2: 1$



We know that in an equilateral triangle centroid coincides with the circumcentre. Therefore, $G$ is the centre of the circumcircle with circumradius GA.

As per theorem, $G$ is the centre and $G D \perp B C$. Therefore,

$B D=C D$

$=4.5 \mathrm{~cm}$

In $\triangle A D B$ we have

$A D^{2}=A B^{2}-D B^{2}$

$=9^{2}-(4.5)^{2}$

$=\sqrt{81-\frac{81}{4}}$

$=\frac{9 \sqrt{3}}{2} \mathrm{~cm}$

Therefore radius $A G=\frac{2}{3} A D=3 \sqrt{3} \mathrm{~cm}$

Question 8: Given an arc of a circle, complete the circle.

Solution. Let PQ be an arc of the circle.

In order to complete the circle. First of all we have to find out its centre and radius.

Now take a point $R$ on the arc $P Q$ and join $P R$ and $Q R$.

Draw the perpendicular bisectors of $P R$ and $Q R$ respectively.

Let these perpendicular bisectors intersect at point $O$.

Then $O P=O Q$, draw a circle with centre $O$ and radius $O P=O Q$ to get the required circle.



Question 9: Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?

Solution. Given that two different pairs of circles $C_{1}\left(O_{1}, r_{1}\right), C_{2}\left(O_{2}, r_{2}\right), C_{3}\left(O_{3}, r_{3}\right)$ and $C_{4}\left(O_{4}, r_{4}\right)$ in the figure.

As we see that only two points $A, B$ of first pair of circle and $C, D$ of the second pair of circles are common points.

Thus only two points are common in each pair of circle.



Question 10: Suppose you are given a circle. Give a construction to find its centre.

Solution. Given a circle $C(O, r)$

We take three points $A, B$ and $C$ on the circle.

Join $A B$ and $B C$.

Draw the perpendicular bisector of chord $A B$ and $B C$.

Let these bisectors intersect at point $O$.

Hence, $O$ is the centre of circle.



Question 11: The lengths of two parallel chords of a circle are $6 \mathrm{~cm}$ and $8 \mathrm{~cm}$. If the smaller chord is at a distance of $4 \mathrm{~cm}$ from the centre, what is the distance of the other chord from the centre?

Solution. Let $A B$ and $C D$ be two parallel chord of the circle with centre $O$ such that $A B=6 \mathrm{~cm}, C D=8 \mathrm{~cm}$ and $O P=4 \mathrm{~cm}$. let the radius of the circle be $r \mathrm{~cm}$.

According to the question, we have to find $O Q$



Draw $O P \perp A B$ and $O Q \perp C D$ as well as point $O, Q$, and $P$ are collinear.

Let $O Q=x$

Join $O A$ and $O C$, then

$O A=O C=r$

Now $O P \perp A B$ and $O Q \perp C D$

So, $A P=3 \mathrm{~cm}$ and $C Q=4 \mathrm{~cm}$

In $\triangle O A P$ we have

$O A^{2}=O P^{2}+A P^{2}$

$r^{2}=4^{2}+3^{2}$

$=16+9$

$=25$

$r=\sqrt{25}$

$=5$

And in $\Delta O C Q$

$O Q^{2}=O C^{2}-C Q^{2}$

$=O A^{2}-C Q^{2}$

$=5^{2}-4^{2}$

$=25-16$

$=9$

$O Q=\sqrt{9}$

$3 \mathrm{~cm}$

Question 12 : Two chords $A B, C D$ of lengths $5 \mathrm{~cm}, 11 \mathrm{~cm}$ respectively of a circle are parallel, If the distance between $A B$ and $C D$ is $3 \mathrm{~cm}$, find the radius of the circle.

Solution. Let $A B$ and $C D$ be two parallel chord of the circle with centre $O$ such that $A B=5 \mathrm{~cm}$ and $C D=11$ $\mathrm{cm}$. let the radius of the circle be $r \mathrm{~cm}$.



Draw $O P \perp A B$ and $O Q \perp C D$ as well as point $O, Q$ and $P$ are collinear.

Clearly, $P Q=3 \mathrm{~cm}$

Let $O Q=x$ then $O P=x+3$

In $\Delta O A P$ and $\Delta O C Q$ we have

$O A^{2}=O P^{2}+A P^{2}$

\Rightarrow r^{2}=(x+3)^{2}+\left(\frac{5}{2}\right)^{2} \cdots \cdots(1)

And

$O C^{2}=O Q^{2}+C Q^{2}$

$\Rightarrow r^{2}=x^{2}+\left(\frac{11}{2}\right)^{2} \ldots$(2)

From (1) and (2) we get

$(x+3)^{2}+\left(\frac{5}{2}\right)^{2}=x^{2}+\left(\frac{11}{2}\right)^{2}$

$\Rightarrow x^{2}+6 x+9+\frac{25}{4}=x^{2}+\frac{121}{4}$

$\Rightarrow 6 x+\frac{61}{4}=\frac{121}{4}$

$\Rightarrow 6 x=\frac{121-61}{4}$

$\Rightarrow 6 x=\frac{60}{4}$

$\Rightarrow x=\frac{5}{2}$

Putting the value of $x$ in $(2)$ we get,

$r^{2}=\left(\frac{5}{2}\right)^{2}+\left(\frac{11}{2}\right)^{2}$

$=\frac{25}{4}+\frac{121}{4}$

$=\frac{146}{4}$

$\Rightarrow r=\sqrt{\frac{146}{4}}$

$r=\frac{\sqrt{146}}{2} \mathrm{~cm}$

Question 13: Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.

Solution. Let $P$ is the mid point of chord $A B$ of circle $C(O, r)$ then according to question, line $O Q$ passes through the point $P$.

Then prove that $O Q$ bisect the $\operatorname{arc} A B$.

Join $O A$ and $O B$.



In $\triangle A O P$ and $\triangle B O P$

$O A=O B$

(Radii of the same circle)

$A P=B P$

(P is the mid point of chord $A B$ )

$O P=O P$

(Common)

Therefore, $\triangle A O P \cong \Delta B O P$

$\Rightarrow \angle A O P=\angle B O P$

(by cpct)

Thus

$\operatorname{Arc} A Q=\operatorname{arc} B Q$

Therefore, OQ bisect the arc AB

Hence Proved.

Question 14: Prove that two different circles cannot intersect each other at more than two points.

Solution. We have to prove that two different circles cannot intersect each other at more than two points.

Let the two circles intersect in three points $A, B$ and $C$.

Then as we know that these three points $A, B$ and $C$ are non-collinear. So, a unique circle passes through these three points.

This is a contradiction to the fact that two given circles are passing through $A, B, C$.

Hence, two circles cannot intersect each other at more than two points.

Hence, proved.

Question 15: Two chords $A B$ and $C D$ of lengths $5 \mathrm{~cm}$ and $11 \mathrm{~cm}$ respectively of a circle are parallel to each other and are opposite side of its centre. If the distance between $A B$ and $C D$ is $6 \mathrm{~cm}$, find the radius of the circle.

Solution. Let $A B$ and $C D$ be two parallel chord of the circle with centre $O$ such that $A B=5 \mathrm{~cm}, C D=11 \mathrm{~cm}$ and $P Q=6 \mathrm{~cm}$. Let the radius of the circle be $r \mathrm{~cm}$.



Draw $O P \perp A B$ and $O Q \perp C D$ as well as point $O, Q$, and $P$ are collinear.

Clearly, $P Q=6 \mathrm{~cm}$

Let $O Q=x \mathrm{~cm}$ then

$O P=6-x$

Join $O A$ and $O C$, then

$O A=O C=r$

Now $O P \perp A B$ and $O Q \perp C D$

So, $A P=\frac{5}{2} \mathrm{~cm}$ and $C Q=\frac{11}{2} \mathrm{~cm}$

In $\Delta O A P$ and $\triangle O C Q$ we have

$O A^{2}=O P^{2}+A P^{2}$

$\Rightarrow r^{2}=x^{2}+\left(\frac{5}{2}\right)^{2} \ldots$(1)

And

$O C^{2}=O Q^{2}+C Q^{2}$

$\Rightarrow r^{2}=(6-x)^{2}+\left(\frac{11}{2}\right)^{2} \ldots \ldots$92)

From (1) and (2) we get

$x^{2}+\left(\frac{5}{2}\right)^{2}=(6-x)^{2}+\left(\frac{11}{2}\right)^{2}$

$\Rightarrow x^{2}+\frac{25}{4}=36-12 x+x^{2}+\frac{121}{4}$

$12 x=\left(36+\frac{121}{4}\right)-\frac{25}{4}$

$12 x=\frac{144+121}{4}-\frac{25}{4}$

$=\frac{265-25}{4}$

$=\frac{240}{4}$

$=60$

$x=\frac{60}{12}$

$=5$

Putting the value of $x$ in (1) we get,

$r^{2}=(5)^{2}+\left(\frac{5}{2}\right)^{2}$

$=25+\frac{25}{4}$

$=\frac{100+25}{4}$

$r=\sqrt{\frac{125}{4}}$

$=\frac{5 \sqrt{5}}{2} \mathrm{~cm}$

Question 1: Three girls Ishita, Isha and Nisha are playing a game by standing on a circle of radius $20 \mathrm{~m}$ drawn in a park. Ishita throws a ball to Isha, Isha to Nisha and Nisha to Ishita. If the distance between Ishita and Isha and between Isha and Nisha is $24 \mathrm{~m}$ each, what is the distance between Ishita and Nisha.

Solution. Using the data given in the question we can draw a diagram that looks like fig (1).



From the figure we see that it is an isosceles triangle that has been circumscribed in a circle of radius $R$ $=20 \mathrm{~m}$

The equal sides of the isosceles triangle measure $24 \mathrm{~m}$ in length. The length of the base of the isosceles triangle is what we are required to find out.

Since it is an isosceles triangle the perpendicular dropped from the vertex $A$ to the base will pass though the circumcentre of the triangle. Let ' $h$ ' be the height of the triangle.

Since the triangle has been circumscribed by a circle of radius ' $R$ ' the length of the distances from ' $O$ ' to any of the three persons would be ' $R$ '.

Let the positions of the persons Isha, Ishita and Nisha be replaced by ' $A$ ', ' $B$ ' and ' $C$ ' respectively. And let the length of the unknown base be, $B C=2 x \mathrm{~m}$.

This is shown in the fig $(2)$.

Now, consider the triangle $\triangle B O D$, we have

$R^{2}=(h-R)^{2}+x^{2}$

$R^{2}=h^{2}-2 h R+R^{2}+x^{2}$

$2 h R=h^{2}+x^{2}$

$R=\frac{h^{2}+x^{2}}{2 h}$

$R=\frac{h^{2}+x^{2}}{2 h}$

At the same time consider $\triangle A B D$, we have

$h^{2}+x^{2}=24^{2}$

$h^{2}+x^{2}=576$

Substitute this value in equation we got for ' $R$ ', we get

$R=\frac{h^{2}+x^{2}}{2 h}$

$=\frac{576}{2 h}$

$h=\frac{576}{2 R}$

$=\frac{576}{(2)(20)}$

$=14.4$

Now we have got the value of the height of the triangle as $h=14.4 \mathrm{~m}$.

Substituting the value of $h$ in the below equation,

$h^{2}+x^{2}=24^{2}$

$x^{2}=576-h^{2}$

$x^{2}=576-(14.4)^{2}$

$x^{2}=576-207.36$

$x^{2}=368.64$

$x=19.2$

Now we have the value of $x=19.2 \mathrm{~m}$

We need the value of $B C$

$B C=2 x$

$=2(19.2)$

$=38.4$

Hence, the distance between Ishita and Nisha is $38.4 \mathrm{~m}$.

Question 2: A circular park of radius $40 \mathrm{~m}$ is situated in a colony. Three boys Ankur, Amit and hands to talk to each other. Find the length of the string of each phone.

Solution. From the given data, we see that the given situation is equivalent to an equilateral triangle circumscribed by a circle.

Let the positions of the three boys Ankur, Amit and Anand be denoted by the points ' $A$ ', ' $B$ ' and ' $C$ '. Let ' $O$ ' be the centre of the circle, ' $a$ ' is the sides of the equilateral triangle and ' $R$ ' is its circumradius.



Now, in an equilateral triangle with side ' $a$ ', the height, ' $h$ ' of the equilateral triangle would be,

$A B=B C=C A$

Therefore, $\Delta A B C$ is an equilateral triangle.

$O A=40 \mathrm{~m}$

Medians of equilateral triangle pass through the circumcentre $(\mathrm{O})$ of the equilateral triangle $A B C$. We know that medians intersect each other in the ratio $2: 1$. As $A D$ is the median of equilateral triangle $A B C$, we can write

$\frac{O A}{O D}=\frac{2}{1}$

$\Rightarrow \frac{40}{O D}=\frac{2}{1}$’

$\Rightarrow O D=20 \mathrm{~m}$

$A D=A O+O D=(40+20) \mathrm{m}=60 \mathrm{~m}$

In $\triangle A D C$,

$A C^{2}=A D^{2}+D C^{2}$

$\Rightarrow A C^{2}=(60)^{2}+\frac{A C^{2}}{4}$

$\left[\because A C=B C, D C=\frac{1}{2} B C \Rightarrow D C=\frac{1}{2} A C\right]$

$\Rightarrow \frac{3 A C^{2}}{4}=3600$

$\Rightarrow A C^{2}=4800$

$\Rightarrow A C=40 \sqrt{3} \mathrm{~m}$

Hence the length of the string of each phone is $40 \sqrt{3} \mathrm{~m}$

Question 1: Fill in the blanks:

(i) All points lying inside/outside a circle are called points /......points.

(ii) Circles having the same centre and different radii are called .... circles.

(iii) A point whose distance from the centre of a circle is greater than its radius lies in $\ldots$ of the circle.

(iv) A continuous piece of a circle is………..of the circle.

(v) The longest chord of a circle is a …... of the circle.

(vi) An arc is a……when its ends are the ends of a diameter.

(vii) Segment of a circle is the region between an arc and ....of the circle.

(viii) A circle divides the plane, on which it lies, in $\ldots$ parts.

Solution. (i) interior/exterior

(ii) concentric

(iii) the exterior

(iv) arc

(v) diameter

(vi) semi-circle

(vii) centre

(viii) three

Question 2: Write the truth value (T/F) fo the following with suitable reasons:

(i) A circle is a plane figure.

(ii) Line segment joining the centre to any point on the circle is a radius of the circle.

(iii) If a circle is divided into three equal arcs each is a major arc.

(iv) A circle has only finite number of equal chords.

(v) A chord of a circle, which is twice as long is its radius is a diameter of the circle.

(vi) Sector is the region between the chord and its corresponding arc.

(vii) The degree measure of an arc is the complement of the central angle containing the arc.

(viii) The degree measure of a semi-circle is $180^{\circ}$

Solution. (i) Given that a circle is a plane figure.

As we know that a circle is a collection of those points in a plane that are at a given constant distance from a fixed point in the plane.

Thus the given statement is true

(ii) Given that line segment joining the centre to any point on the circle is a radius of the circle.

As we know that line segment joining the centre to any point on the circle is a radius of the circle.

Thus the given statement is true .

(iii) Given that if a circle is divided into three equal arcs each is a major arc.

As we know that if points $P, Q$ and $R$ lies on the given circle $C(O, r)$ in such a way that

$l(\widehat{P Q})=l(\widehat{Q R})=l(\widehat{R P})$

Then each arc is called major arc.

Thus the given statement is true .

(iv) It is given that a circle has only finite number of equal chords.

As we know that a circle having infinite num

Thus the given statement is false

(v) Given that a chord of the circle, which is twice as long as its radius is diameter of the circle.

As we know that a chord of a circle which is largest to others and passing through the centre of the circle and twice as long as its radius is called diameter of the circle.

Thus the given statement is true

(vi) It is given that sector is the region between the chord and its corresponding arc.

As we know that the region between the chord and its corresponding arc is called sector.

Thus the given statement is true

(vii) Given that the degree measure of an arc is the complement of the central angle containing the arc.

As we know that the degree measure of a minor arc is the measure of the central angle containing the arc and that of a major arc is $360^{\circ}$ minus the degree measure of the corresponding minor arc.

Let degree measure of an arc $\widehat{P Q}$ is $\theta$ of a given circle $C(O, r)$ is denoted by $m(\widetilde{P Q})=\theta$

Thus the given statement is false

(viii) Given that the degree measure of a semi-circle is $180^{\circ}$.

As we know that the diameter of a circle divides into two equal parts and each of these two arcs are known as semi-circle.

$\widehat{P Q}$ and $\widehat{Q P}$ are semi circle

Hence,

$m(\widehat{P Q})=m(\widehat{Q P})=180^{\circ}$

Thus the given statement is true .

Question 1: In the given figure, $O$ is the centre of the circle. If $\angle A P B=50^{\circ}$, find $\angle A O B$ and $\angle O A B$.



Solution. This question seems to be incorrect.

Question 2: In the given figure, $O$ is the centre of the circle. Find $\angle B A C$.



Solution. It is given that

$\angle B O A=80^{\circ}$ And $\angle A O C=110^{\circ}$ (given)



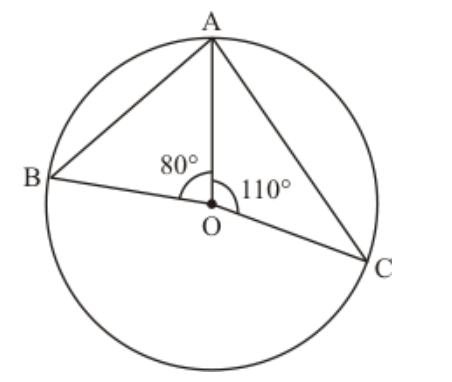
We have to find $\angle B A C$

In given triangle $\triangle B O A$

$\angle B O A=80^{\circ}$ (Given)

$O B=O A$

(Radii of the same circle)

Therefore, $\triangle B O A$ is an isosceles triangle.

So, $\angle O B A=\angle O A B \ldots (1)$

$\angle A O B+\angle O B A+\angle B A O=180^{\circ}$

$80^{\circ}+\angle O B A+\angle B A O=180^{\circ}$

(Given $\angle B O A=80^{\circ}$ )

$80^{\circ}+2(\angle B A O)=180^{\circ}$

[From (1)]

So

$2(\angle B A O)=180^{\circ}-80^{\circ}$

$=100^{\circ}$

Again from figure, $\triangle A O C$ is given triangle and $\angle C O A=110^{\circ}$

Now in $\triangle A O C$,

$O A=O C$

(Radii of the same circle)

$\angle O A C=\angle O C A$

$\angle A O C+\angle O C A+\angle O A C=180^{\circ}$

$110^{\circ}+\angle O C A+\angle O A C=180^{\circ}$

(Given that $\angle A O C=80^{\circ}$ )

$110^{\circ}+2(\angle O A C)=180^{\circ}$

$=2(\angle O A C)$

$=180^{\circ}-110^{\circ}$

$=70^{\circ}$

Then,

$\angle O A C=\frac{70^{\circ}}{2}$

$=35^{\circ}$

Since

$\angle B A C=\angle B A O+\angle O A C$

$=50^{\circ}+35^{\circ}$

$=85^{\circ}$

Hence $\angle B A C=85^{\circ}$

Question 3: If $O$ is the centre of the circle, find the value of $x$ in each of the following figures.

(i)



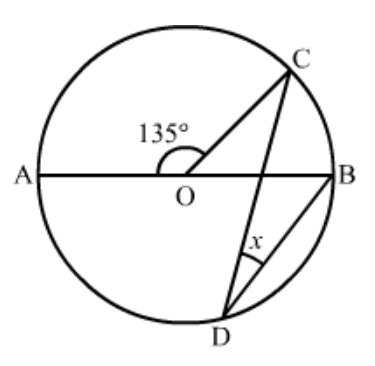
(ii)



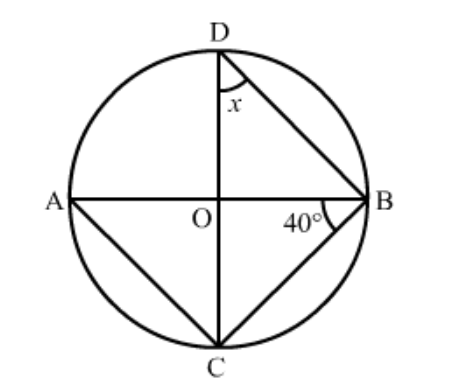
(iii)



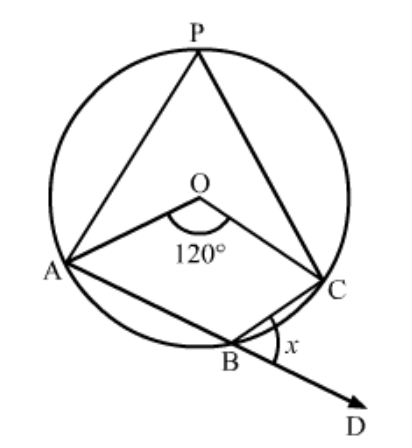
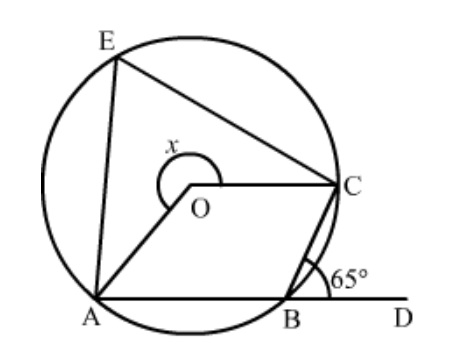
(i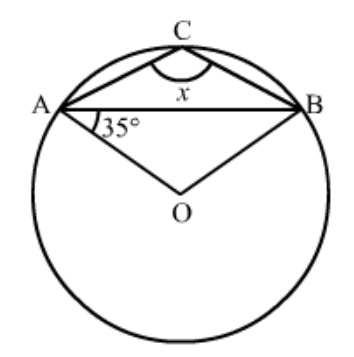v)



(v)



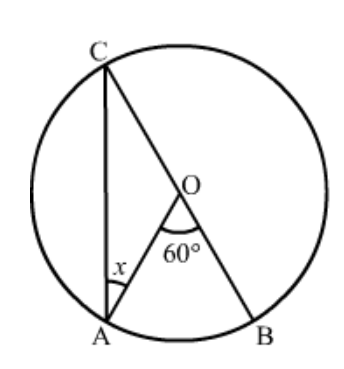
(vi)



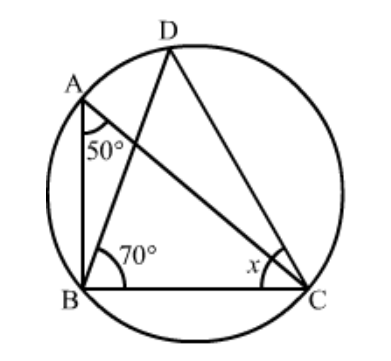
(vii)



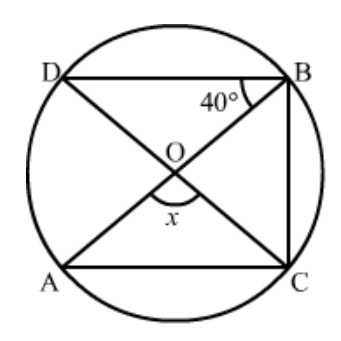
(viii)



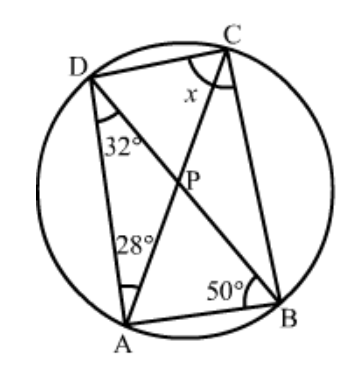
(ix)



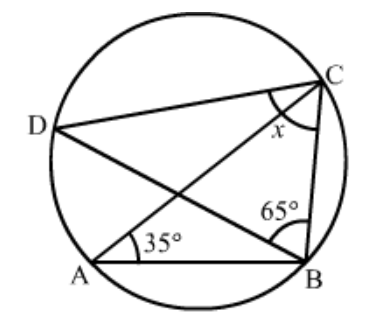
(x)



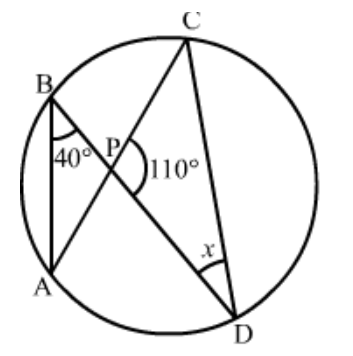
(xi)



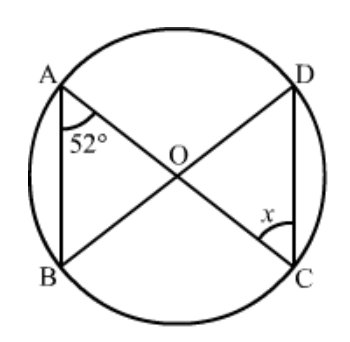
(xii)



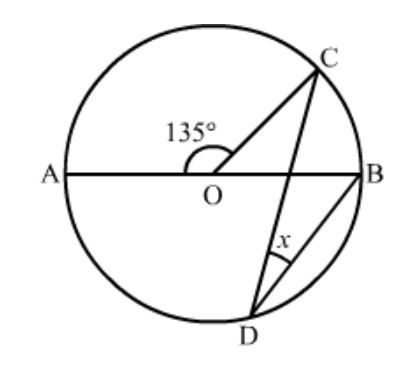
Solution. We have to find $x$ in each figure.

(i) It is given that $\angle A O C=135^{\circ}$

$\angle A O C+\angle C O B=180^{\circ}$

[Linear pair]

$\angle C O B=180^{\circ}-135^{\circ}$

$=45^{0}$



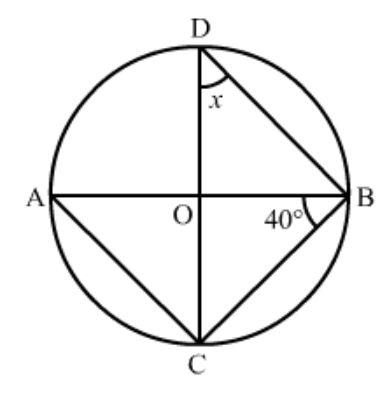
As we know the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

Now , $x=\frac{1}{2} \angle C O B=22 \frac{1}{2}^{\circ}$

Hence $x=22 \frac{1}{2}^{0}$

(ii) As we know that $\angle C A B=\angle C D B=x$

[Angles in the same segment]

line $A B$ is diameter passing through centre,

So,

$\angle B C A=90^{\circ}$

[Angle inscribed in a semicircle is a right angle ]



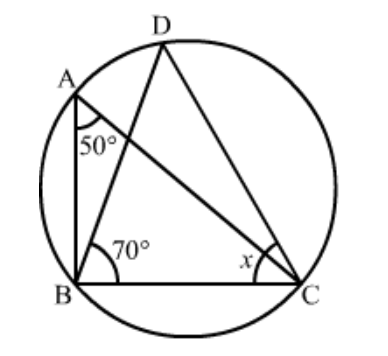
$\angle C A B+\angle A B C+\angle B C A=180^{\circ}$

[Angle sum property]

$\Rightarrow x+40^{\circ}+90^{\circ}=180^{\circ}$

$\Rightarrow \angle C O A=120^{\circ}$

$\Delta O C A$ is an isosceles triangle.

So

$\angle C A O=\frac{1}{2}\left(180^{\circ}-120^{\circ}\right)$

$=30^{\circ}$

Hence, $x=30^{\circ}$

(vii) $\angle B A C=\angle B D C$

(Angle in the same segment)



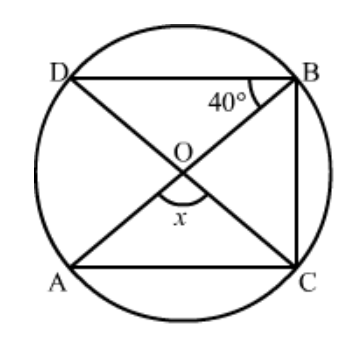
In $\Delta B D C$ we have

$\angle D B C+\angle B D C+\angle B C D=180^{\circ}$

$70^{\circ}+50^{\circ}+\angle B C D=180^{\circ}$

$\angle B C D=180^{\circ}-120^{\circ}$

$=60^{\circ}$

Hence $x=60^{\circ}$

(viii)



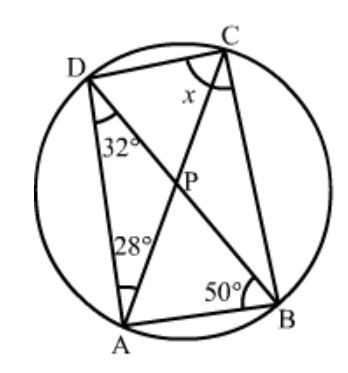
As $O D=O B \quad$ (Radius of circle)

Therefore, $\triangle D O B$ is an isosceles triangle.

$\angle O D B+\angle O B D+\angle D O B=180^{\circ}$

$40^{\circ}+40^{\circ}+\angle D O B=180^{\circ}$

$\angle D O B=180^{\circ}-80^{\circ}$

$=100^{\circ}$

So $\angle A O C=\angle D O B$

(Vertically opposite angles)

Hence, $x=100^{\circ}$

(ix) It is given that $\angle A B D=50^{\circ}$



$\angle D C A=\angle A B D=50^{\circ} \cdots \cdots$(1)

(Angle in the same segment)

$\angle A D B=\angle A C B=32^{\circ}\ldots \ldots(2)$

(Angle in the same segment)

Because $\angle D C A$ and $\angle A B D$ are on the same segment $A D$ of the circle.

Now from equation $(1)$ and $(2)$ we have

$\angle D C B=50^{\circ}+32^{0}$

$=82^{\circ}$

Hence, $x=82^{\circ}$

(x) It is given that $\angle A=35^{\circ}$



$\angle B A C=\angle B D C=35^{\circ}$

(Angle in the same segment)

Now in $\triangle B D C$ we have

$\angle B D C+\angle D C B+\angle C B D=180^{\circ}$

$\Rightarrow 35^{\circ}+65^{\circ}+\angle C B D=180^{\circ}$

$\Rightarrow \angle C B D=180^{\circ}-100^{\circ}=80^{\circ}$

Hence, $x=80^{\circ}$

$(\mathrm{Xi})$



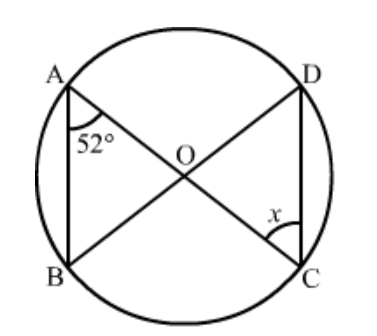
$\angle A B C=\angle A C D=40^{\circ}$

(Angle in the same segment)

In $\triangle P C D$ we have

$\angle C P D+\angle P C D+\angle P D C=180^{\circ}$

$40^{\circ}+110^{\circ}+\angle P D C=180^{\circ}$

$\angle P D C=180^{\circ}-150^{\circ}$

$=30^{\circ}$

Hence $x=30^{\circ}$

(xii)



$\angle B A O=\angle C D O=52^{\circ}$

(Angle in the same segment)

$\Delta D O C$ is an isosceles triangle

So, $O D=O C$

(Radius of the same circle)

Then $\angle O D C=\angle O C D=52^{\circ}$

Hence $x=52^{\circ}$

Question 4: $O$ is the circumcentre of the triangle $A B C$ and $O D$ is perpendicular on $B C$. Prove that $\angle B O D=\angle A$

Solution. We have to prove that $\angle B O D=\angle A$



Since, circumcenter is the intersection of perpendicular bisectors of each side of the triangle.

Now according to figure $A, B, C$ are the vertices of $\triangle A B C$

In $\triangle B O C, O D$ is perpendicular bisector of $B C$

So, $B D=C D$

$O B=O C$

(Radius of the same circle)

And,

$\mathrm{OD}=\mathrm{OD}$

(Common)

Therefore,

$\triangle B D O \cong \triangle C D O$ (SSS congruency criterion)

$\angle B O D=\angle C O D$ (by cpct)

We know that angle formed any chord of the circle at the center is twice of the angle formed at the circumference by same chord

Therefore,

$\angle B A C=\frac{1}{2} \angle B O C$

$\Rightarrow \angle B A C=\frac{1}{2} \times 2 \angle B O D$

$\Rightarrow \angle B A C=\angle B O D$

Therefore,

$\angle B O D=\angle A$

Hence proved

Question 5: In the given figure, $O$ is the centre of the circle, $B O$ is the bisector of $\angle A B C$. Show that $A B=A C$.



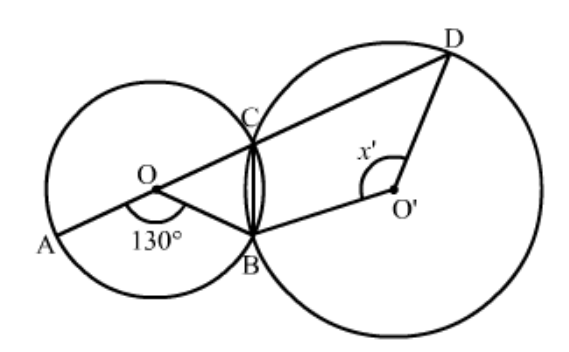
Solution. It is given that, $\angle A B C$ is on circumference of circle $B D$ is passing through centre.



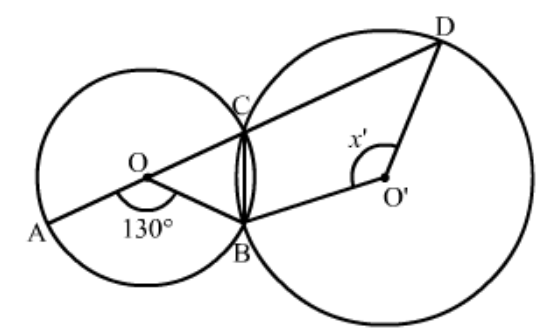
Construction: Join $A$ and $C$ to form $A C$ and extend $B O$ to $D$ such that $B D$ be the perpendicular bisector of $A C$.

Now in $\triangle B D A$ and $\triangle B D C$ we have

$\mathrm{AD}=\mathrm{CD}$

( $B D$ is the perpendicular bisector)

So $\angle B D A=\angle B D C=90^{\circ}$

$B D=B D$ (Common)

$\triangle B D A \cong \triangle B D C$

(SAS congruency criterion)

Hence $A B=B C$

(by cpct)

Question 6: In the given figure, $O$ and $O$ ' are centres of two circles intersecting at $B$ and $C$. $A C D$ is a straight line, find $x$.



Solution. It is given that

Two circles having center $O$ and $O$ ' and $\angle A O B=130^{\circ}$

And $A C$ is diameter of circle having center $O$



We have

$\angle A C B=\frac{1}{2} \angle A O B=65^{\circ}$

So

$\angle D C B=180^{\circ}-\angle A C B$

$=180^{\circ}-65^{0}$

$=115^{0}$

Now, reflex $\angle B O^{\prime} D=2 \angle B C D$

So

$360^{\circ}-x^{o}=2 \times 115$

$=230^{\circ}$

$x^{\circ}=360^{\circ}-230^{\circ}=130^{\circ}$

Hence, $x=130^{\circ}$

Question 7: In the given figure, if $\angle A C B=40^{\circ}, \angle D P B=120^{\circ}$, find $\angle C B D$.



Solution. It is given that $\angle A C B=40^{\circ}$ and $\angle D P B=120^{\circ}$



Construction: Join the point $A$ and $B$

$\angle A C B=\angle A D B=40^{\circ}$

(Angle in the same segment)

Now in $\triangle B D P$ we have

$\angle D P B+\angle P B D+\angle B D P=180^{\circ}$

$\Rightarrow 120^{\circ}+\angle P B D+40^{\circ}=180^{\circ}$

$\Rightarrow \angle P B D=20^{\circ}$

Hence $\angle C B D=20^{\circ}$

Question 8: A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

Solution. We have to find $\angle A D B$ and $\angle A E B$



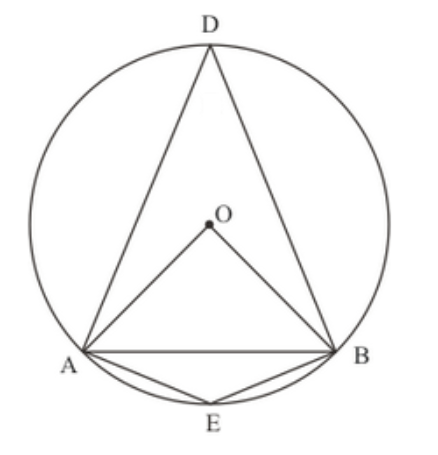
Construction: - $O$ is centre and $r$ is radius and given that chord is equal to radius of circle

Now in $\triangle A O B$ we have

$\mathrm{AO}=\mathrm{OB}=\mathrm{BA}$

( It is given that chord is equal to radius of circle)

So, $\triangle A O B$ is an equilateral triangle

$\angle A O B=60^{\circ}$

So, $\angle A O B=2 \angle A D B$

(The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle)

Then $\angle A D B=30^{\circ}$

So

$\angle A E B=\frac{1}{2}($ Reflex $\angle A O B)$

$=\frac{1}{2}\left(360^{\circ}-60^{\circ}\right)$

$=150^{\circ}$

Therefore,

$\angle A D B=30^{\circ}$ and $\angle A E B=150^{\circ}$

Hence, the angle subtended by the chord at a point on the minor arc is $150^{\circ}$ and also at a point on the major arc is $30^{\circ}$.

Question 9: In the given figure, it is given that $O$ is the centre of the circle and $\angle A O C=150^{\circ}$. Find $\angle A B C$.



Solution. It is given that $O$ is the centre of circle and $A, B$ and $C$ are points on circumference.

$\angle A O C=150^{\circ}$ (Given)



We have to find $\angle A B C$

The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

$\angle A B C=\frac{1}{2}($ reflex $\angle A O C)$

$=\frac{1}{2}\left(360^{\circ}-150^{\circ}\right)$

$=\frac{1}{2} \times 210^{\circ}$

$=105^{\circ}$

Hence, $\angle A B C=105^{\circ}$

Question 10: In the given figure, $O$ is the centre of the circle, prove that $\angle x=\angle y+\angle Z$.



Solution. It is given that, $O$ is the center of circle and $A, B$ and $C$ are points on circumference on triangle



We have to prove that $\angle x=\angle y+\angle z$

$\angle 4$ and $\angle 3$ are on same segment

So, $\angle 4=\angle 3$

$\angle x=2 \angle 3$

(Angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle)

$\angle x=\angle 4+\angle 3 \ldots$(1)

$\angle y=\angle 3+\angle 1$(Exterior angle is equal to the sum of two opposite interior angles)……(2)

$\angle 4=\angle z+\angle 1$

(Exterior angle is equal to the sum of two opposite interior angles)

$\angle z=\angle 4-\angle 1 \ldots \ldots$ (3)

Adding $(2)$ and $(3)$

$\angle y+\angle z=\angle 3+\angle 4 \ldots$(4)

From equation (1) and (4) we have

$\angle x=\angle y+\angle z$

Question 11: In the given figure, $O$ is the centre of a circle and $P Q$ is a diameter. If $\angle R O S=40^{\circ}$, find $\angle R T S$.

/media/uploads/2021/11/rd-sharma-chaper-15-img-155.png

Solution. It is given that $O$ is the centre and $\angle R O S=40^{\circ}$

/media/uploads/2021/11/rd-sharma-chaper-15-img-156.png

We have $\angle R Q S=\frac{1}{2} \angle R O S=20^{\circ}$

In right angled triangle $R Q T$ we have

$\angle R Q T+\angle Q T R+\angle T R Q=180^{\circ}$

$\Rightarrow 20^{\circ}+\angle Q T R+90^{\circ}=180^{\circ}$

$\Rightarrow \angle Q T R=70^{\circ}$

Hence, $\angle R T S=70^{\circ}$

Also Read,

Download NCERT Class 9 Maths Chapterwise Book PDF

Download NCERT Class 10 Maths Chapterwise Book PDF

Download NCERT Class 9 Maths Chapterwise Exemplar PDF

Download Class 10 Maths Chapterwise Exemplar PDF

If you have any Confusion related to RD Sharma Solutions for Class 9 Maths Chapter 16 Circles, then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App