JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advanced Questions
Paragraph for Questions 10 and 11
The general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous axis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless stick, as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed , the motion at any instant can be taken as a combination of (i) a rotation of the centre of mass of the disc about the z-axis, and (ii) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed $\omega$ in this case.
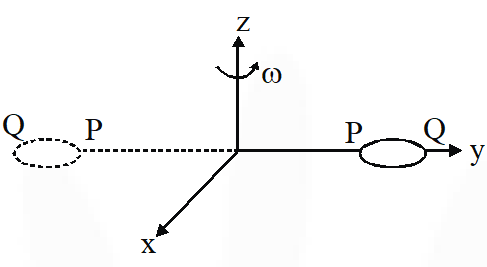 Now consider two similar systems as shown in the figure : case (A) the disc with its face vertical and parallel to x-z plane; Case (B) the disc with its face making an angle of $45^{\circ}$ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed about the z-axis.
Now consider two similar systems as shown in the figure : case (A) the disc with its face vertical and parallel to x-z plane; Case (B) the disc with its face making an angle of $45^{\circ}$ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed about the z-axis.
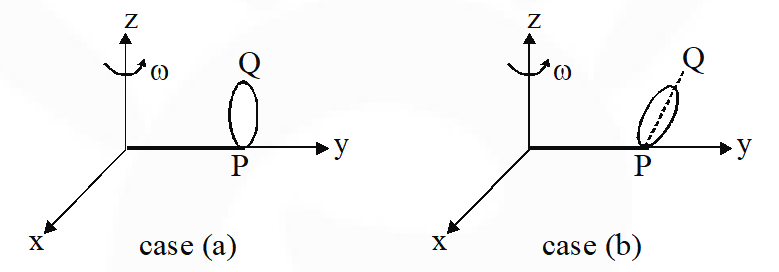 Paragraph 1
A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity is an example of a non-inertial frame of reference. The relationship between the force $\overrightarrow{\mathrm{F}}_{\mathrm{rot}}$ experienced by a particle of mass m moving on the rotating disc and the force $\overrightarrow{\mathrm{F}}_{\mathrm{in}}$ experienced by the particle in an inertial frame of reference is
$\overrightarrow{\mathrm{F}}_{\mathrm{rot}}=\overrightarrow{\mathrm{F}}_{\mathrm{in}}+2 \mathrm{m}\left(\overrightarrow{\mathrm{v}}_{\mathrm{rot}} \times \vec{\omega}\right)+\mathrm{m}(\vec{\omega} \times \overrightarrow{\mathrm{r}}) \times \vec{\omega}$
where $\vec{v}_{\text {rot }}$ is the velocity of the particle in the rotating frame of reference and $\overrightarrow{\mathrm{r}}$ is the position
vector of the particle with respect to the centre of the disc.
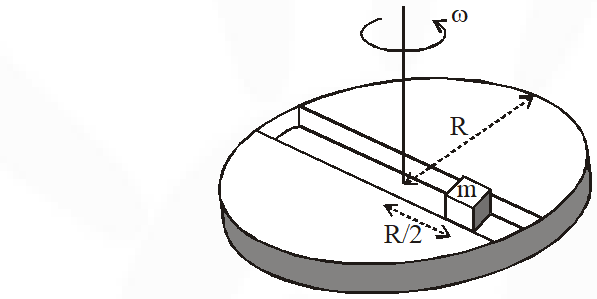
Now consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed about its vertical axis through its center. We assign a coordinate system with the origin at the centre of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\vec{\omega}=\omega \hat{k})$ A small block of mass m is gently placed in the slot at $\overrightarrow{\mathrm{r}}=(\mathrm{R} / 2) \hat{\mathrm{i}}$ at $\mathrm{t}=0$ and is constrained to move only along the slot.
Paragraph 1
A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity is an example of a non-inertial frame of reference. The relationship between the force $\overrightarrow{\mathrm{F}}_{\mathrm{rot}}$ experienced by a particle of mass m moving on the rotating disc and the force $\overrightarrow{\mathrm{F}}_{\mathrm{in}}$ experienced by the particle in an inertial frame of reference is
$\overrightarrow{\mathrm{F}}_{\mathrm{rot}}=\overrightarrow{\mathrm{F}}_{\mathrm{in}}+2 \mathrm{m}\left(\overrightarrow{\mathrm{v}}_{\mathrm{rot}} \times \vec{\omega}\right)+\mathrm{m}(\vec{\omega} \times \overrightarrow{\mathrm{r}}) \times \vec{\omega}$
where $\vec{v}_{\text {rot }}$ is the velocity of the particle in the rotating frame of reference and $\overrightarrow{\mathrm{r}}$ is the position
vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed about its vertical axis through its center. We assign a coordinate system with the origin at the centre of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\vec{\omega}=\omega \hat{k})$ A small block of mass m is gently placed in the slot at $\overrightarrow{\mathrm{r}}=(\mathrm{R} / 2) \hat{\mathrm{i}}$ at $\mathrm{t}=0$ and is constrained to move only along the slot.
 Paragraph for Questions 27 and 28
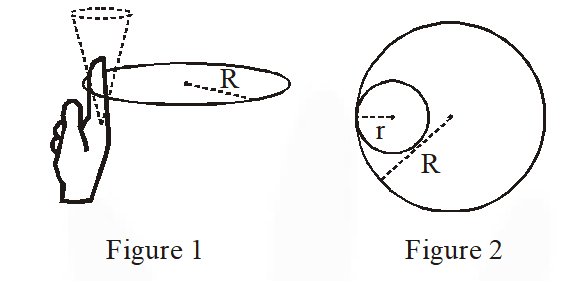
One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $\omega_{0}$. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is µ and the acceleration due to gravity is g.
Paragraph for Questions 27 and 28
One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $\omega_{0}$. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is µ and the acceleration due to gravity is g.
Q. A block of base 10 cm × 10 cm and height 15 cm is kept on an inclined plane. The coefficient of friction between them is $\sqrt{3}$. The inclination $\theta$ of this inclined plane from the horizontal plane is gradually increased from $0^{\circ}$. Then :-
(A) at $\theta=30^{\circ}$, the block will start sliding down the plane
(B) the block will remain at rest on the plane up to certain $\theta$ and then it will topple
(C) at $\theta=60^{\circ}$, the block will start sliding down the plane and continue to do so at higher angles
(D) at $\theta=60^{\circ}$, the block will start sliding down the plane and on further increasing q, it will topple at certain q
[IIT-JEE 2009]
Ans. (B)
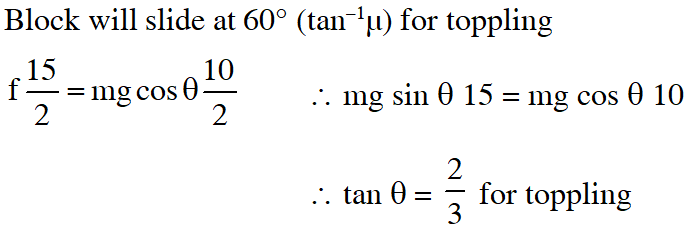
Q. If the resultant of the external forces acting on a system of particles is zero, then from an inertial frame, one can surely say that
(A) linear momentum of the system does not change in time
(B) kinetic energy of the system does not change in time
(C) angular momentum of the system does not change in time
(D) potential energy of the system does not change in time
[IIT-JEE 2009]
Ans. (A)
Q. A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
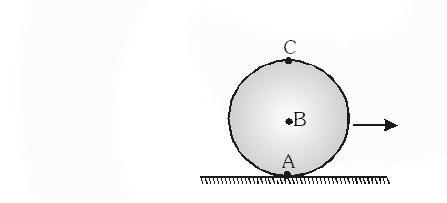 (A) $\vec{v}_{C}-\vec{v}_{A}=2\left(\vec{v}_{B}-\vec{v}_{C}\right)$
(B) $\vec{v}_{C}-\vec{v}_{B}=\vec{v}_{B}-\vec{v}_{A}$
(C) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=2\left|\vec{v}_{B}-\vec{v}_{C}\right|$
(D) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=4\left|\vec{v}_{B}\right|$
[IIT-JEE 2009]
(A) $\vec{v}_{C}-\vec{v}_{A}=2\left(\vec{v}_{B}-\vec{v}_{C}\right)$
(B) $\vec{v}_{C}-\vec{v}_{B}=\vec{v}_{B}-\vec{v}_{A}$
(C) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=2\left|\vec{v}_{B}-\vec{v}_{C}\right|$
(D) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=4\left|\vec{v}_{B}\right|$
[IIT-JEE 2009]
 (A) $\vec{v}_{C}-\vec{v}_{A}=2\left(\vec{v}_{B}-\vec{v}_{C}\right)$
(B) $\vec{v}_{C}-\vec{v}_{B}=\vec{v}_{B}-\vec{v}_{A}$
(C) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=2\left|\vec{v}_{B}-\vec{v}_{C}\right|$
(D) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=4\left|\vec{v}_{B}\right|$
[IIT-JEE 2009]
(A) $\vec{v}_{C}-\vec{v}_{A}=2\left(\vec{v}_{B}-\vec{v}_{C}\right)$
(B) $\vec{v}_{C}-\vec{v}_{B}=\vec{v}_{B}-\vec{v}_{A}$
(C) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=2\left|\vec{v}_{B}-\vec{v}_{C}\right|$
(D) $\left|\vec{v}_{C}-\vec{v}_{A}\right|=4\left|\vec{v}_{B}\right|$
[IIT-JEE 2009]
Ans. (B,C)
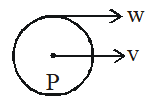
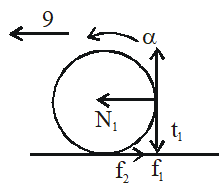
Q. A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2N on the ring and rolls it without slipping with an acceleration of 0.3 $\mathrm{m} / \mathrm{s}^{2}$. The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is (P/10). The value of P is
 [IIT-JEE 2011]
[IIT-JEE 2011]
 [IIT-JEE 2011]
[IIT-JEE 2011]
Ans. 4
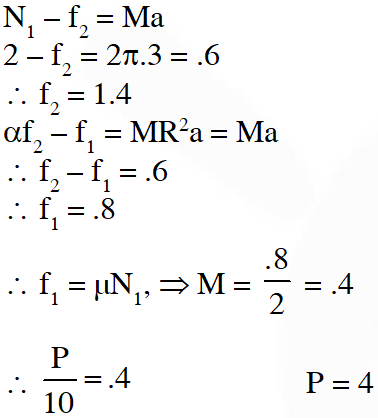

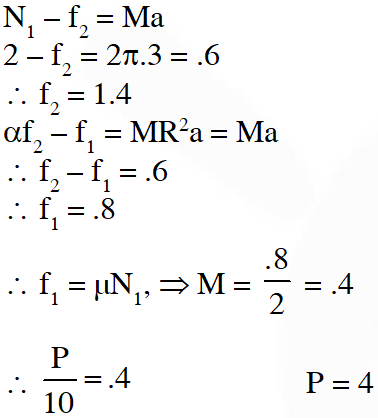
Q. Four solid spheres each of diameter $\sqrt{5}$ cm and mass 0.5 kg are placed with their centers at the
corners of a square of side 4 cm. The moment of inertia of the system about the diagonal of the square is $\mathrm{N} \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}$, then N is
[IIT-JEE 2011]
Ans. 9
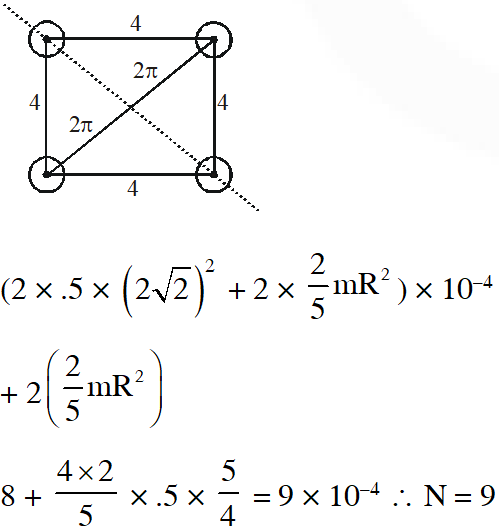
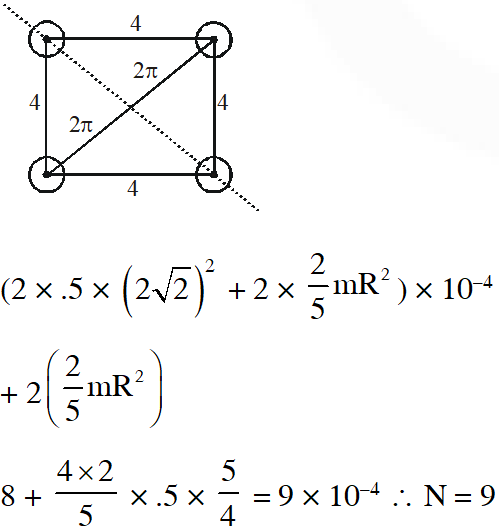
Q. A thin ring of mass 2 kg and radius 0.5 m is rolling without slipping on a horizontal plane with velocity 1 m/s. A small ball of mass 0.1 kg, moving with velocity 20 m/s in the opposite direction, hits the ring at a height of 0.75 m and goes vertically up with velocity 10 m/s. Immediately after the collision
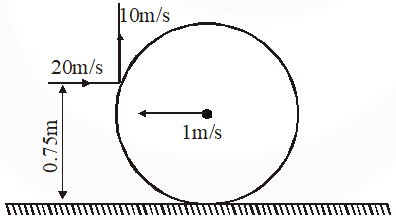 (A) the ring has pure rotation about its stationary CM
(B) the ring comes to a complete stop
(C) friction between the ring and the ground is to the left
(D) there is no friction between the ring and the ground
[IIT-JEE 2011]
(A) the ring has pure rotation about its stationary CM
(B) the ring comes to a complete stop
(C) friction between the ring and the ground is to the left
(D) there is no friction between the ring and the ground
[IIT-JEE 2011]
 (A) the ring has pure rotation about its stationary CM
(B) the ring comes to a complete stop
(C) friction between the ring and the ground is to the left
(D) there is no friction between the ring and the ground
[IIT-JEE 2011]
(A) the ring has pure rotation about its stationary CM
(B) the ring comes to a complete stop
(C) friction between the ring and the ground is to the left
(D) there is no friction between the ring and the ground
[IIT-JEE 2011]
Ans. (A,C or C)
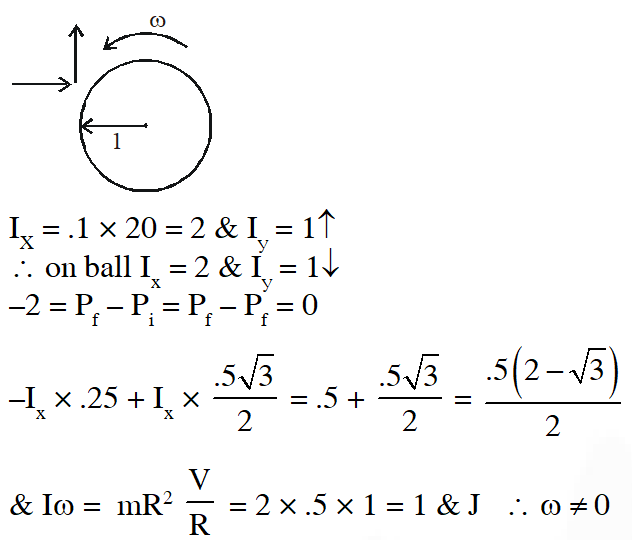
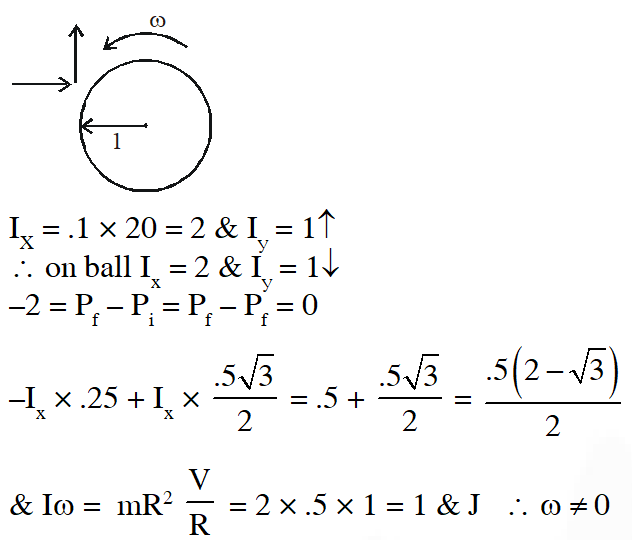
Q. A thin uniform rod, pivoted at OP, is rotating in the horizontal plane with constant angular speed $\omega$. as shown in the figure. At time t = 0, a small insect starts from O and moves with constant speed v with respect to the rod towards the other end. If reaches the end of the rod at t = T and stops. The angular speed of the system remains $\omega$ throughout. The magnitude of the torque $(|\tau|)$ on the system about O, as a function of time is best represented by which plot?
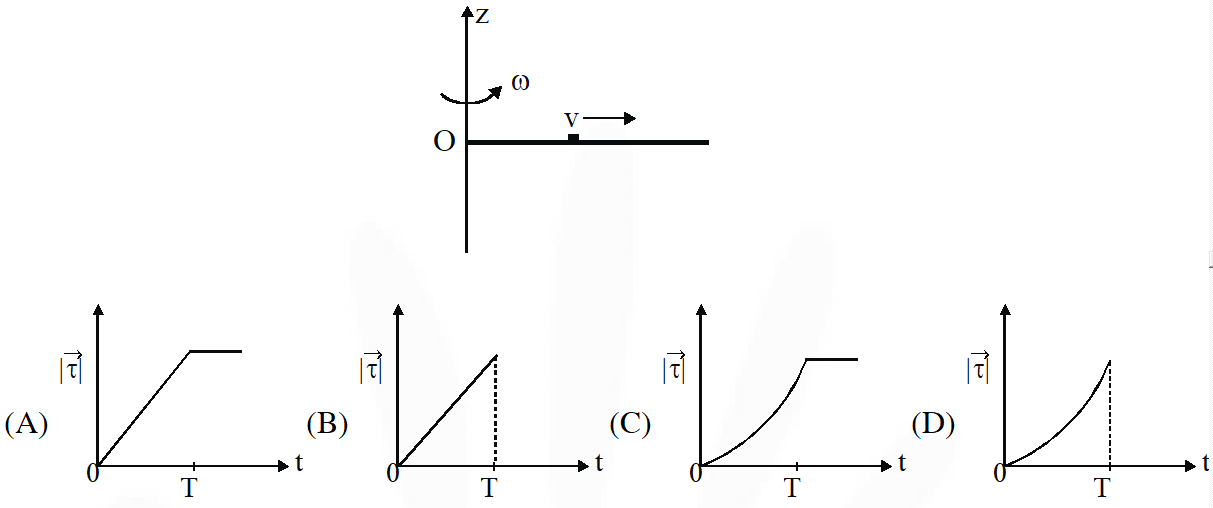 [IIT-JEE 2012]
[IIT-JEE 2012]
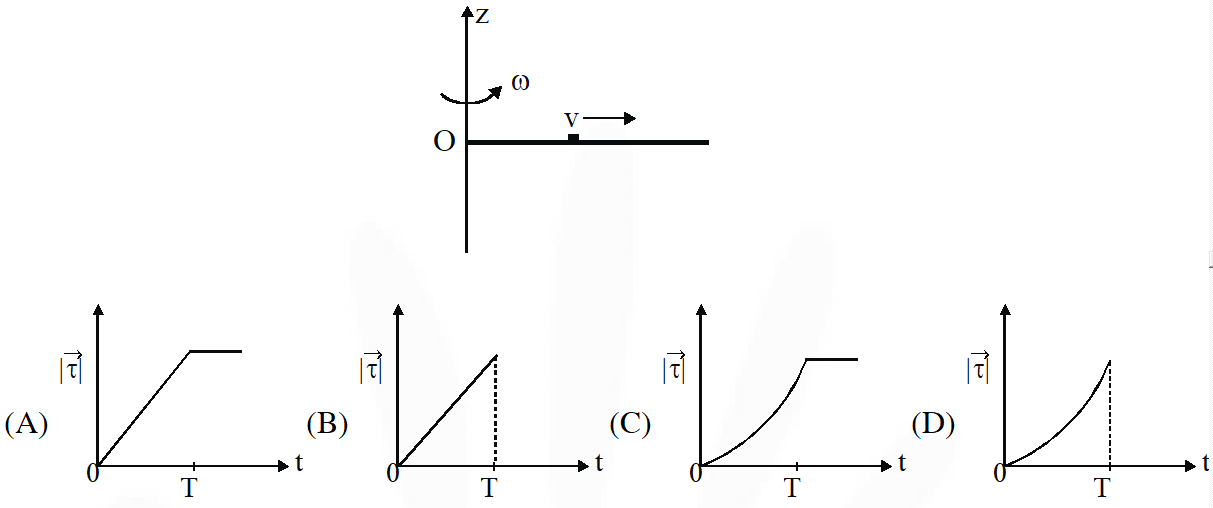 [IIT-JEE 2012]
[IIT-JEE 2012]
Ans. (B)
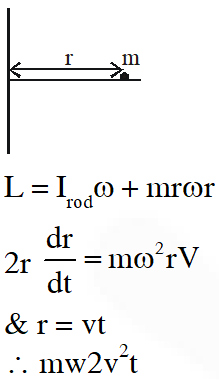
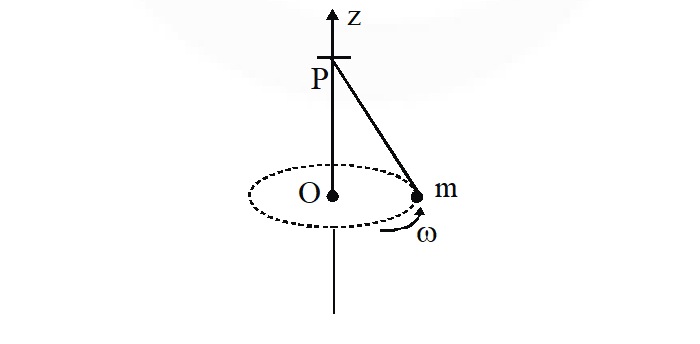
Q. A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed $\omega$. If the angular momentum of the system, calculated about O and P are denoted by $\vec{L}_{o}$ and $\vec{L}_{p}$ respectively, then
 (A) $\vec{L}_{o}$ and $\vec{L}_{p}$ do not vary with time
(B) $\vec{L}_{o}$ varies with time while $\vec{L}_{p}$ remains constant
(C) $\vec{L}_{o}$ remains constant while $\vec{L}_{P}$ varies with time
(D) $\vec{L}_{o}$ and $\vec{L}_{P}$ both vary with time
[IIT-JEE 2012]
(A) $\vec{L}_{o}$ and $\vec{L}_{p}$ do not vary with time
(B) $\vec{L}_{o}$ varies with time while $\vec{L}_{p}$ remains constant
(C) $\vec{L}_{o}$ remains constant while $\vec{L}_{P}$ varies with time
(D) $\vec{L}_{o}$ and $\vec{L}_{P}$ both vary with time
[IIT-JEE 2012]
 (A) $\vec{L}_{o}$ and $\vec{L}_{p}$ do not vary with time
(B) $\vec{L}_{o}$ varies with time while $\vec{L}_{p}$ remains constant
(C) $\vec{L}_{o}$ remains constant while $\vec{L}_{P}$ varies with time
(D) $\vec{L}_{o}$ and $\vec{L}_{P}$ both vary with time
[IIT-JEE 2012]
(A) $\vec{L}_{o}$ and $\vec{L}_{p}$ do not vary with time
(B) $\vec{L}_{o}$ varies with time while $\vec{L}_{p}$ remains constant
(C) $\vec{L}_{o}$ remains constant while $\vec{L}_{P}$ varies with time
(D) $\vec{L}_{o}$ and $\vec{L}_{P}$ both vary with time
[IIT-JEE 2012]
Ans. (C)
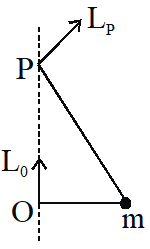
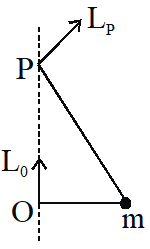
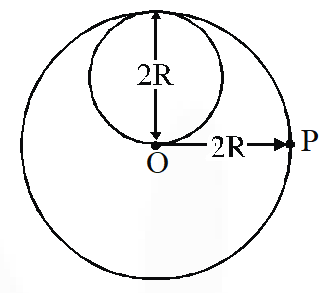
Q. A lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes assing through O and P is $\mathrm{I}_{0}$ and $\mathrm{I}_{\mathrm{P}}$ respectively. Both these axes are perpendicular to the plane of the lamina. The ratio $\frac{I_{P}}{I_{O}}$ to the nearest integer is
 [IIT-JEE 2012]
[IIT-JEE 2012]
 [IIT-JEE 2012]
[IIT-JEE 2012]
Ans. 3
$\mathrm{I}_{0}=\mathrm{I}_{\text {biggle }}-\mathrm{I}_{\text {mall }}$
$=\frac{4 \mathrm{m}(2 \mathrm{R})^{2}}{2}-\left(\frac{\mathrm{mR}^{2}}{2}+\mathrm{mR}^{2}\right)$
$=8 \mathrm{mR}^{2}-\frac{3}{2} \mathrm{mR}^{2}=\frac{13}{2} \mathrm{mR}^{2}$
$\mathrm{I}_{\mathrm{P}}=\left(\frac{4 \mathrm{m}(2 \mathrm{R})^{2}}{2}+4 \mathrm{m}(2 \mathrm{R})^{2}\right)-\left(\frac{\mathrm{mR}^{2}}{2}+\mathrm{m} 4 \mathrm{R}^{2}\right)=20-\frac{1}{2}=\frac{39}{2}$
$\therefore$ ratio $=\frac{39}{13}=3$
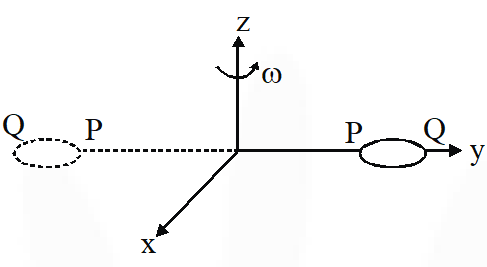 Now consider two similar systems as shown in the figure : case (A) the disc with its face vertical and parallel to x-z plane; Case (B) the disc with its face making an angle of $45^{\circ}$ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed about the z-axis.
Now consider two similar systems as shown in the figure : case (A) the disc with its face vertical and parallel to x-z plane; Case (B) the disc with its face making an angle of $45^{\circ}$ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed about the z-axis.
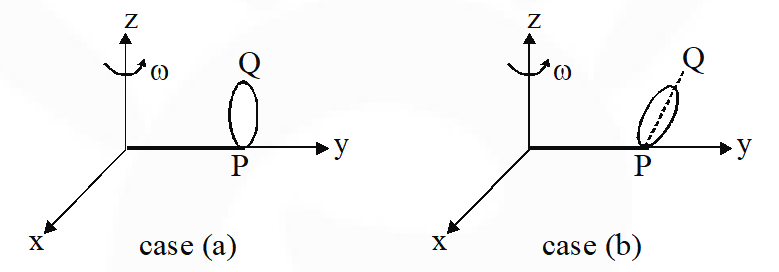
Q. Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
(A) It is $\sqrt{2 \omega}$ for both the cases.
(B) It is $\omega$ for case $(a) ;$ and $\frac{\omega}{\sqrt{2}}$ for case $(b)$
(C) It is $\omega$ for case $(a) ;$ and $\sqrt{2 \omega}$ for case (b).
(D) It is $\omega$ for both the cases.
[IIT-JEE 2012]
Ans. (D)
$\omega$ for both the cases.
$\therefore$ in same t $2 \pi$ angle.
Q. Which of the following statements about the instantaneous axis (passing through the centre of mass) is correct?
(A) It is vertical for both the cases (a) and (b).
(B) It is vertical for case (a); and is at $45^{\circ}$ to the x-z plane and lies in the plane of the disc for case (b).
(C) It is horizontal for case (a); and is at $45^{\circ}$ to the x-z plane and is normal to the plane of the disc for case (b).
(D) It is vertical for case (a); and is at $45^{\circ}$ to the x-z plane and is normal to the plane of the disc for case (b)
[IIT-JEE 2012]
Ans. (A)
vertical for both.
Q. The figure shows a system consisting of (i) a ring of outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed and (ii) an inner disc of radius 2R rotating anti-clockwise with angular speed $\omega /$2. The ring and disc are separated by frictionless ball bearing. The system is in the x-z plane. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of $30^{\circ}$ with the horizontal. Then with respect to the horizontal surface,
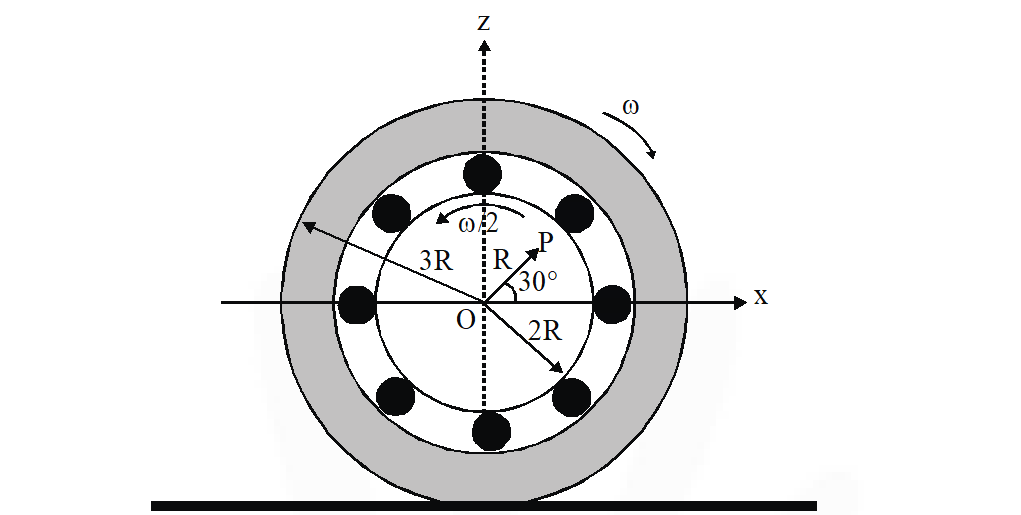 (A) the point O has a linear velocity $3 R \omega \hat{i}$
(B) the point $P$ has a linear velocity $\frac{11}{4} R \omega \hat{i}+\frac{\sqrt{3}}{4} R \omega \hat{k}$
(C) the point P has a linear velocity $\frac{13}{4} R \omega \hat{i}-\frac{\sqrt{3}}{4} R \omega \hat{k}$
(D) the point P has a linear velocity $\left(3-\frac{\sqrt{3}}{4}\right) R \omega \hat{i}+\frac{1}{4} R \omega \hat{k}$
[IIT-JEE 2012]
(A) the point O has a linear velocity $3 R \omega \hat{i}$
(B) the point $P$ has a linear velocity $\frac{11}{4} R \omega \hat{i}+\frac{\sqrt{3}}{4} R \omega \hat{k}$
(C) the point P has a linear velocity $\frac{13}{4} R \omega \hat{i}-\frac{\sqrt{3}}{4} R \omega \hat{k}$
(D) the point P has a linear velocity $\left(3-\frac{\sqrt{3}}{4}\right) R \omega \hat{i}+\frac{1}{4} R \omega \hat{k}$
[IIT-JEE 2012]
 (A) the point O has a linear velocity $3 R \omega \hat{i}$
(B) the point $P$ has a linear velocity $\frac{11}{4} R \omega \hat{i}+\frac{\sqrt{3}}{4} R \omega \hat{k}$
(C) the point P has a linear velocity $\frac{13}{4} R \omega \hat{i}-\frac{\sqrt{3}}{4} R \omega \hat{k}$
(D) the point P has a linear velocity $\left(3-\frac{\sqrt{3}}{4}\right) R \omega \hat{i}+\frac{1}{4} R \omega \hat{k}$
[IIT-JEE 2012]
(A) the point O has a linear velocity $3 R \omega \hat{i}$
(B) the point $P$ has a linear velocity $\frac{11}{4} R \omega \hat{i}+\frac{\sqrt{3}}{4} R \omega \hat{k}$
(C) the point P has a linear velocity $\frac{13}{4} R \omega \hat{i}-\frac{\sqrt{3}}{4} R \omega \hat{k}$
(D) the point P has a linear velocity $\left(3-\frac{\sqrt{3}}{4}\right) R \omega \hat{i}+\frac{1}{4} R \omega \hat{k}$
[IIT-JEE 2012]
Ans. (A,B)
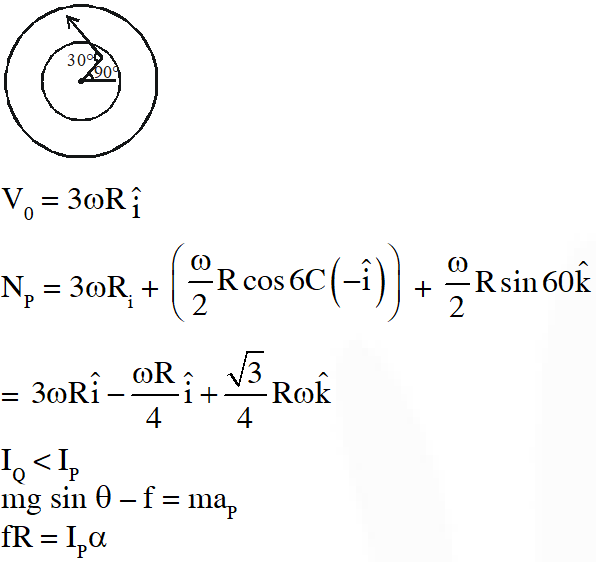
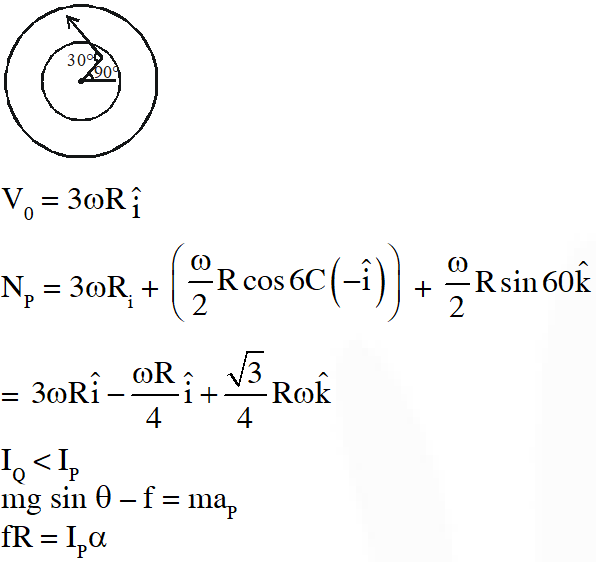
Q. Two solid cylinders P and Q of same mass and same radius start rolling down a fixed inclined plane from the same height at the same time. Cylinder P has most of its mass concentrated near its surface, while Q has most of its mass concentrated near the axis. Which statement(s) is(are) correct?
(A) Both cylinders P and Q reach the ground at the same time.
(B) Cylinder P has larger acceleration than cylinder Q.
(C) Both cylinders reach the ground with same translational kinetic energy.
(D) Cylinder Q reaches the ground with larger angular speed.
[IIT-JEE 2012]
Ans. (D)
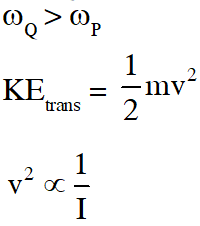
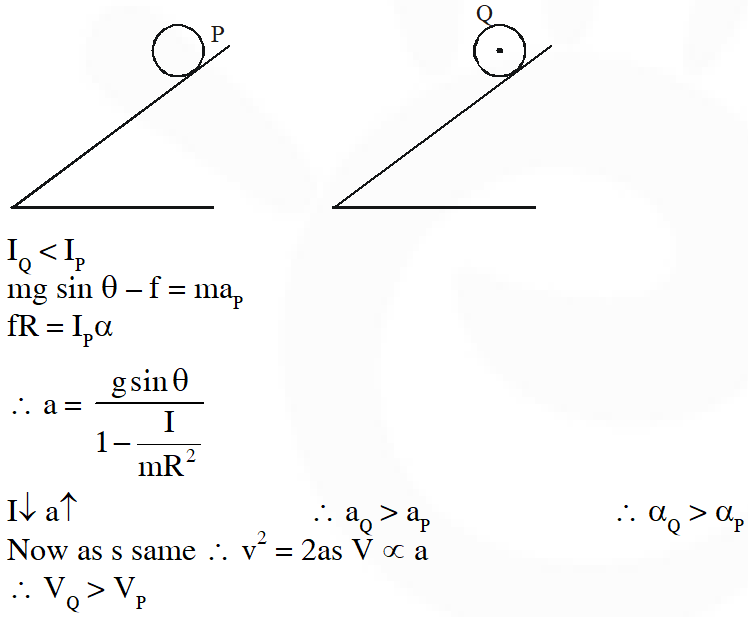
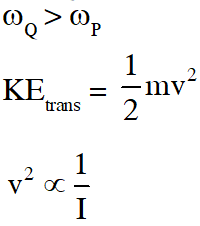
Q. A uniform circular disc of mass 50 kg and radius 0.4 m is rotating with an angular velocity of
10 rad $\mathrm{s}^{-1}$ about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (in rad s–1) of the system is
[IIT-JEE 2013]
Ans. 8
by angular momentum conservation
$\mathrm{I}_{\text {disc }} \omega_{0}=\left(\mathrm{I}_{\text {disc }}+2 \mathrm{I}_{\text {ring }}\right) \omega$
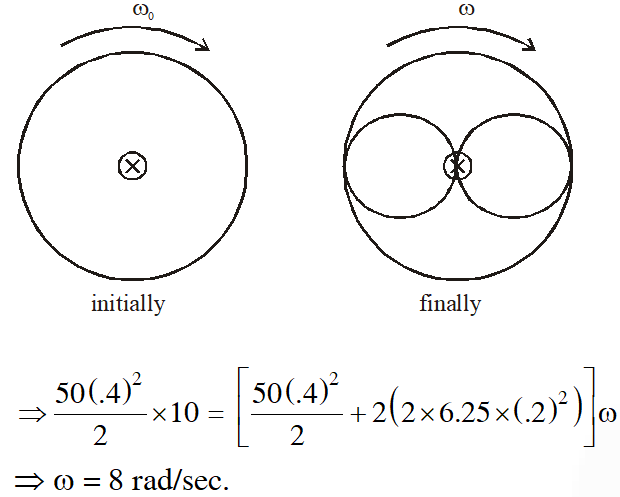
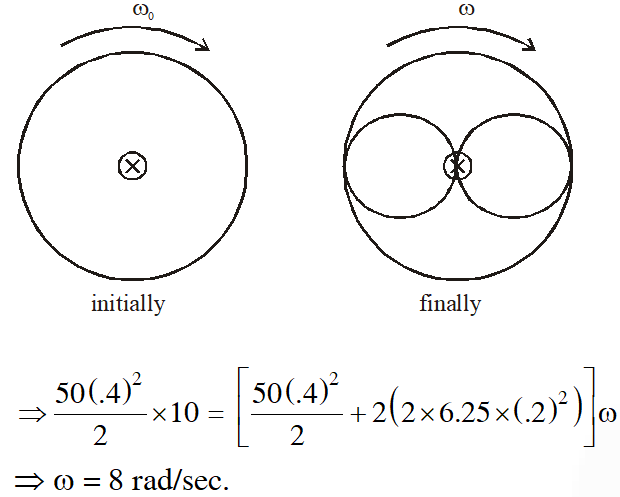
Q. A horizontal circular platform of radius 0.5 m and mass 0.45 kg is free to rotate about its axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25 m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of 9 ms$-1$with respect to the ground. The rotational speed of the platform in rad s$-1$after the balls leave the platform is
 [JEE Advanced-2014]
[JEE Advanced-2014]
 [JEE Advanced-2014]
[JEE Advanced-2014]
Ans. 4
Since no external torque acts therefore angular momentum remains conserved.
Angular momentum of ball = Angular momentum of plateform
$0.05 \times 9 \times 0.25 \times 2=\frac{1}{2} \times 0.45 \times 0.5 \times 0.5 \times \omega$
$\omega=4 \mathrm{rad} / \mathrm{s}$
Q. A uniform circular disc of mass 1.5 kg and radius 0.5 m is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude F = 0.5 N are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure). One second after applying the forces, the angular speed of the disc in rad $\mathrm{s}^{-1}$ is
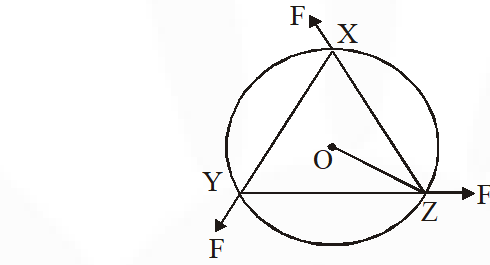 [JEE Advanced-2014]
[JEE Advanced-2014]
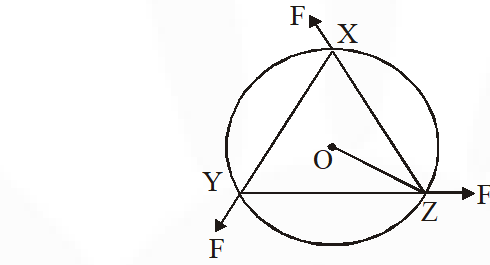 [JEE Advanced-2014]
[JEE Advanced-2014]
Ans. 2
Angular impulse = change in angular momentum
$\tau \Delta \mathrm{t}=\mathrm{I} \omega$
$3 \times \mathrm{F} \times \mathrm{R} \sin 30 \times \Delta \mathrm{t}=\mathrm{I} \omega$
$3 \times 0.5 \times 0.5 \times \frac{1}{2} \times 1=\frac{1}{2} \times 1.5 \times 0.5 \times 0.5 \times \omega$
$\omega=2 \mathrm{rad} / \mathrm{s}$
Q. Two identical uniform discs roll without slipping on two different, surfaces AB and CD (see figure) starting at A and C with linear speeds $\mathrm{v}_{1}$ and $\mathrm{v}_{2}$ respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed and $\mathrm{v}_{1}=3 \mathrm{m} / \mathrm{s},$ then $\mathrm{v}_{2}$ in m/s is (g = 10 $\mathrm{m} / \mathrm{s}^{2}$)
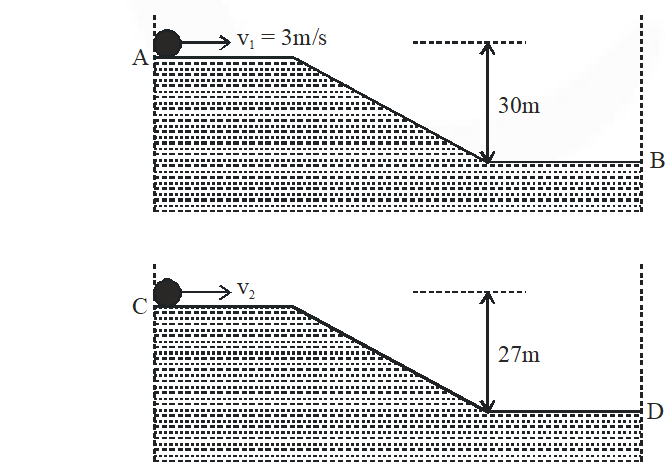 [JEE Advanced-2015]
[JEE Advanced-2015]
 [JEE Advanced-2015]
[JEE Advanced-2015]
Ans. 7
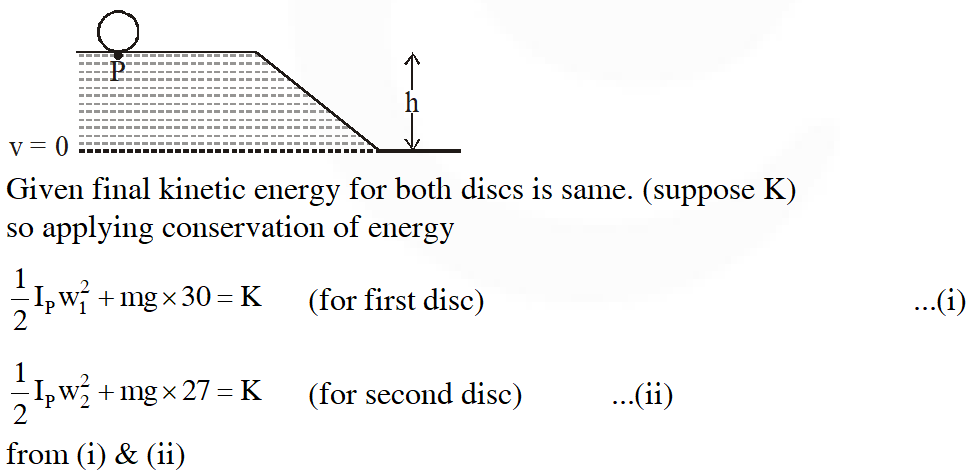
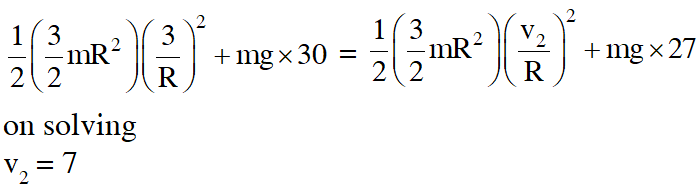
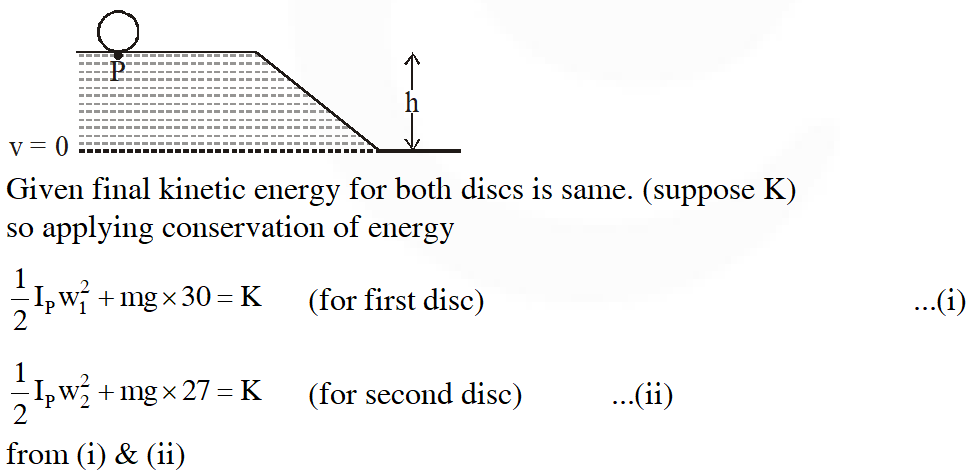
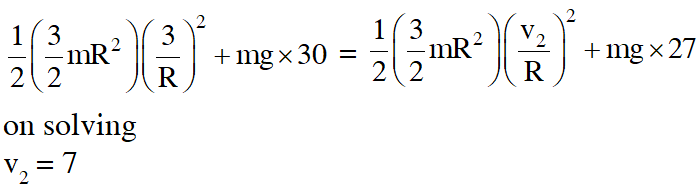
Q. A ring of mass M and radius R is rotating with angular speed $\omega$about a fixed vertical axis passing through its centre O with two point masses each of mass $\frac{\mathrm{M}}{8}$ at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is $\frac{8}{9} \omega$ and one of the masses is at a distance of $\frac{3}{5}$ R from O. At this instant the distance of the other mass from O is :
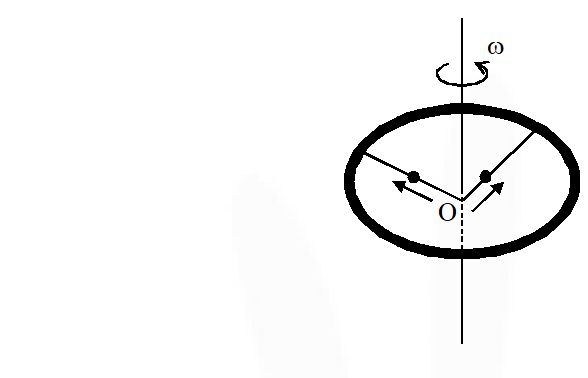 (A) $\frac{2}{3} \mathrm{R}$
(B) $\frac{1}{3} \mathrm{R}$
(C) $\frac{3}{5} \mathrm{R}$
(D) $\frac{4}{5} \mathrm{R}$
[JEE Advanced-2015]
(A) $\frac{2}{3} \mathrm{R}$
(B) $\frac{1}{3} \mathrm{R}$
(C) $\frac{3}{5} \mathrm{R}$
(D) $\frac{4}{5} \mathrm{R}$
[JEE Advanced-2015]
 (A) $\frac{2}{3} \mathrm{R}$
(B) $\frac{1}{3} \mathrm{R}$
(C) $\frac{3}{5} \mathrm{R}$
(D) $\frac{4}{5} \mathrm{R}$
[JEE Advanced-2015]
(A) $\frac{2}{3} \mathrm{R}$
(B) $\frac{1}{3} \mathrm{R}$
(C) $\frac{3}{5} \mathrm{R}$
(D) $\frac{4}{5} \mathrm{R}$
[JEE Advanced-2015]
Ans. (C,D)
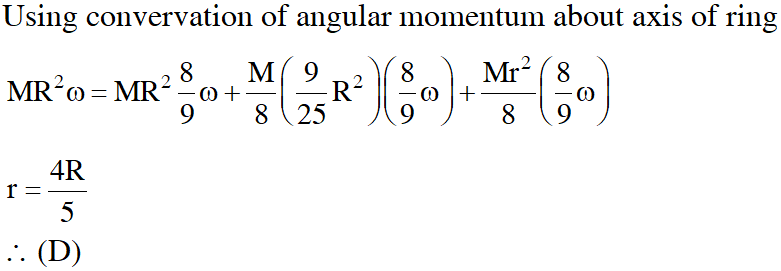
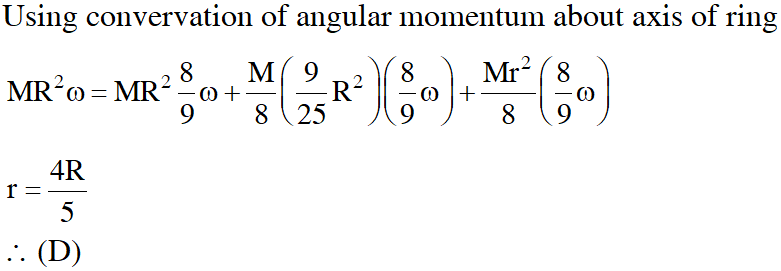
Q. The densities of two solid spheres A and B of the same radii R vary with radial distance r as $\rho_{\mathrm{A}}(\mathrm{r})=\mathrm{k}\left(\frac{\mathrm{r}}{\mathrm{R}}\right)$ and $\rho_{\mathrm{B}}(\mathrm{r})=\mathrm{k}\left(\frac{\mathrm{r}}{\mathrm{R}}\right)^{5}$ , respectively, where k is a constant. The moments of inertia of the indivisual spheres about axes passing through their centres are $\mathrm{I}_{\mathrm{A}}$ and $\mathrm{I}_{\mathrm{B}}$, respectively. If $\frac{\mathrm{I}_{\mathrm{B}}}{\mathrm{I}_{\mathrm{A}}}=\frac{\mathrm{n}}{10}$, the value of n is.
[JEE Advanced-2015]
Ans. 6
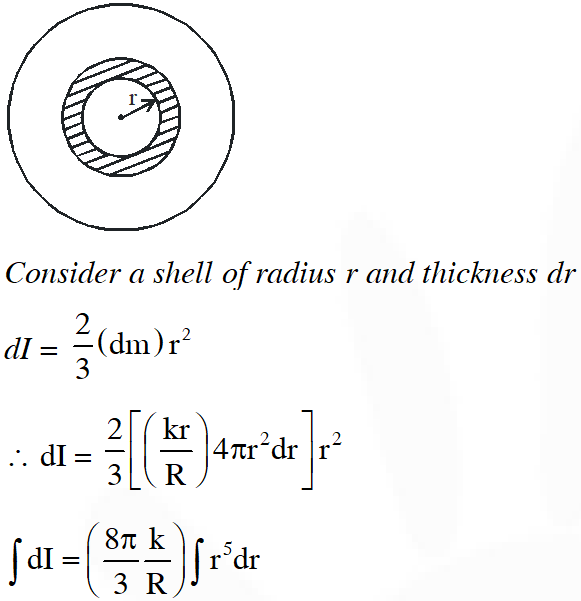
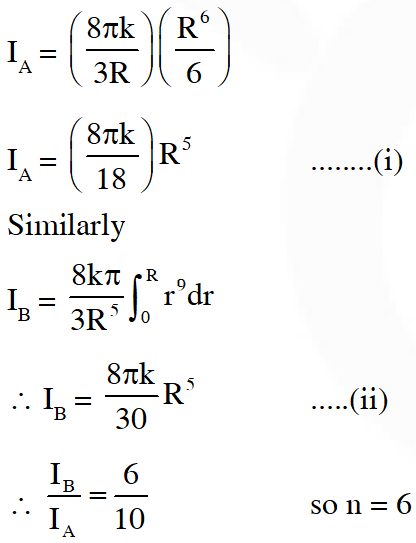
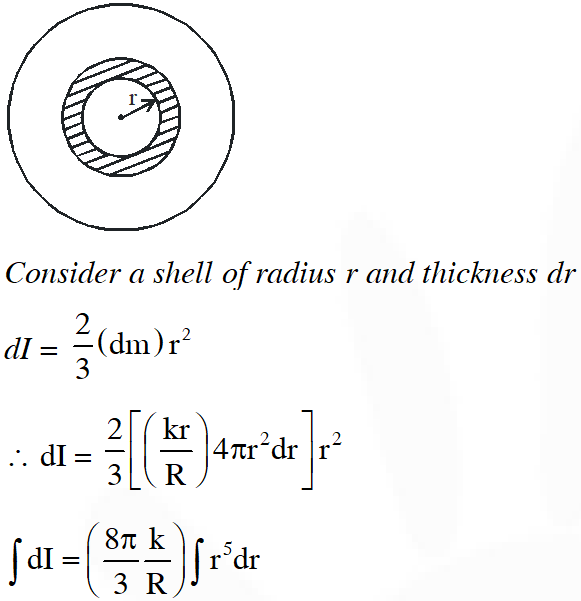
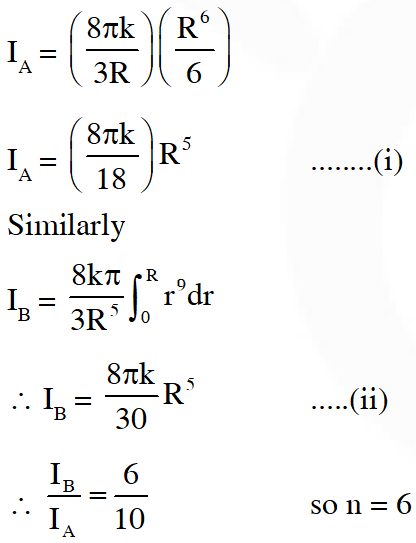
Q. A uniform wooden stick of mass 1.6 kg and length rests in an inclined manner on a smooth, vertical wall of height h (<) such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of $30^{\circ}$ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/ and the frictional force f at the bottom of the stick are: $\left(\mathrm{g}=10 \mathrm{ms}^{-2}\right)$
(A) $\frac{\mathrm{h}}{\ell}=\frac{\sqrt{3}}{16}, \mathrm{f}=\frac{16 \sqrt{3}}{3} \mathrm{N}$
(B) $\frac{\mathrm{h}}{\ell}=\frac{3}{16}, \mathrm{f}=\frac{16 \sqrt{3}}{3} \mathrm{N}$
(C) $\frac{\mathrm{h}}{\ell}=\frac{3 \sqrt{3}}{16}, \mathrm{f}=\frac{8 \sqrt{3}}{3} \mathrm{N}$
(D) $\frac{\mathrm{h}}{\ell}=\frac{3 \sqrt{3}}{16}, \mathrm{f}=\frac{16 \sqrt{3}}{3} \mathrm{N}$
[JEE Advanced-2016]
Ans. (D)

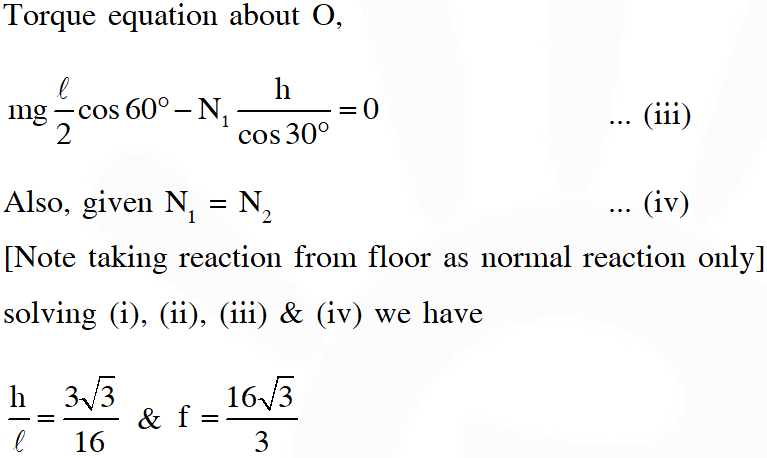

Q. The position vector $\overrightarrow{\mathrm{r}}$ of a particle of mass $\mathrm{m}$ is given by the following equation $\overrightarrow{\mathrm{r}}(\mathrm{t})=\alpha \mathrm{t}^{2} \hat{\mathrm{i}}+\beta t \hat{\mathrm{i}}+\beta t \hat{\mathrm{j}}$
where $\alpha=\frac{10}{3} \mathrm{ms}^{-3}, \beta=5 \mathrm{ms}^{-2}$ and $\mathrm{m}=0.1 \mathrm{kg} .$ At $\mathrm{t}=1 \mathrm{s},$ which of the following statement(s)
is(are) true about the particle?
(A) The velocity $\overrightarrow{\mathrm{v}}$ is given by $\overrightarrow{\mathrm{v}}=(10 \hat{\mathrm{i}}+10 \hat{\mathrm{j}}) \mathrm{ms}^{-1}$
(B) The angular momentum $\overrightarrow{\mathrm{L}}$ with respect to the origin is given by $\overrightarrow{\mathrm{L}}=-\left(\frac{5}{3}\right) \hat{\mathrm{k}} \mathrm{Nms}$
(C) The force $\overrightarrow{\mathrm{F}}$ is given by $\overrightarrow{\mathrm{F}}=(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}) \mathrm{N}$
(D) The torque $\vec{\tau}$ with respect to the origin is given by $\vec{\tau}=-\left(\frac{20}{3}\right) \hat{\mathrm{k}} \mathrm{Nm}$
[JEE Advanced-2016]
Ans. (A,B,D)
$\overrightarrow{\mathrm{r}}=\alpha \mathrm{t}^{3} \hat{\mathrm{i}}+\beta \mathrm{t}^{2} \hat{\mathrm{j}}$
$\overrightarrow{\mathrm{v}}=\frac{\mathrm{d} \overrightarrow{\mathrm{r}}}{\mathrm{dt}}=3 \alpha \mathrm{t}^{2} \hat{\mathrm{i}}+2 \beta \hat{\mathrm{t} \hat{\mathrm{j}}}$
$\overrightarrow{\mathrm{a}}=\frac{\mathrm{d}^{2} \overrightarrow{\mathrm{r}}}{\mathrm{dt}^{2}}=6 \alpha t \hat{\mathrm{i}}+2 \beta \hat{\mathrm{j}}$
At t = 1
(A) $\overrightarrow{\mathrm{v}}=3 \times \frac{10}{3} \times 1 \hat{\mathrm{i}}+2 \times \mathrm{J} \times 1 \hat{\mathrm{j}}$
$=10 \hat{\mathrm{i}}+10 \hat{\mathrm{j}}$
$(\mathrm{B}) \quad \overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}$
$=\left(\frac{10}{3} \times 1 \hat{i}+5 \times 1 \hat{j}\right) \times 0.1(10 \hat{i}+10 \hat{j})$
$=-\frac{5}{3} \hat{\mathrm{k}}$
(C) $\overrightarrow{\mathrm{F}}=\mathrm{m} \times\left(6 \times \frac{10}{3} \times 1 \hat{\mathrm{i}}+2 \times 5 \hat{\mathrm{j}}\right)=2 \hat{\mathrm{i}}+\hat{\mathrm{j}}$
$(\mathrm{D}) \vec{\tau}=\mathrm{r} \times \overrightarrow{\mathrm{F}}$
$=\left(\frac{10}{3} \hat{\mathrm{i}}+5 \hat{\mathrm{j}}\right) \times(2 \hat{\mathrm{i}}+\hat{\mathrm{j}})$
$=+\frac{10}{3} \hat{\mathrm{k}}+10(-\hat{\mathrm{k}})$
$=-\frac{20}{3} \hat{\mathrm{k}}$
Q. Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, right rod of length $\ell=\sqrt{24} \mathrm{a}$ throught their center. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is $\omega$. The angular momentum of the entire assembly about the point 'O' is (see the figure). Which of the following statement(s) is(are) true ?
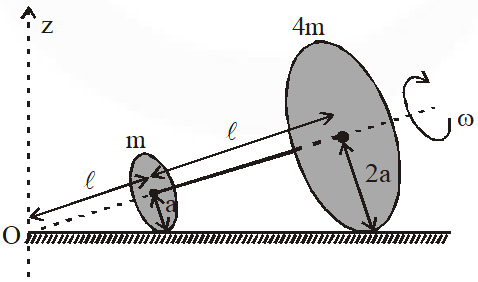 (A) The magnitude of angular momentum of the assembly about its center of mass is $17 \mathrm{ma}^{2} \omega / 2$
(B) The magnitude of the z-component $\overrightarrow{\mathrm{L}}$ is $55 \mathrm{ma}^{2} \omega$
(C) The magnitude of angular momentum of center of mass of the assembly about the point O is 81 $\mathrm{ma}^{2} \mathrm{\omega}$
(D) The center of mass of the assembly rotates about the z-axis with an angular speed of $\omega$/ 5
[JEE Advanced-2016]
(A) The magnitude of angular momentum of the assembly about its center of mass is $17 \mathrm{ma}^{2} \omega / 2$
(B) The magnitude of the z-component $\overrightarrow{\mathrm{L}}$ is $55 \mathrm{ma}^{2} \omega$
(C) The magnitude of angular momentum of center of mass of the assembly about the point O is 81 $\mathrm{ma}^{2} \mathrm{\omega}$
(D) The center of mass of the assembly rotates about the z-axis with an angular speed of $\omega$/ 5
[JEE Advanced-2016]
 (A) The magnitude of angular momentum of the assembly about its center of mass is $17 \mathrm{ma}^{2} \omega / 2$
(B) The magnitude of the z-component $\overrightarrow{\mathrm{L}}$ is $55 \mathrm{ma}^{2} \omega$
(C) The magnitude of angular momentum of center of mass of the assembly about the point O is 81 $\mathrm{ma}^{2} \mathrm{\omega}$
(D) The center of mass of the assembly rotates about the z-axis with an angular speed of $\omega$/ 5
[JEE Advanced-2016]
(A) The magnitude of angular momentum of the assembly about its center of mass is $17 \mathrm{ma}^{2} \omega / 2$
(B) The magnitude of the z-component $\overrightarrow{\mathrm{L}}$ is $55 \mathrm{ma}^{2} \omega$
(C) The magnitude of angular momentum of center of mass of the assembly about the point O is 81 $\mathrm{ma}^{2} \mathrm{\omega}$
(D) The center of mass of the assembly rotates about the z-axis with an angular speed of $\omega$/ 5
[JEE Advanced-2016]
Ans. (A,D)
By no slip condition, here $\omega^{\prime}$ is angular velocity about z axis
$\omega^{\prime} x=\omega r$
$\omega^{\prime}=\frac{\omega r}{x}=\omega \sin \theta=\frac{\omega}{5}$
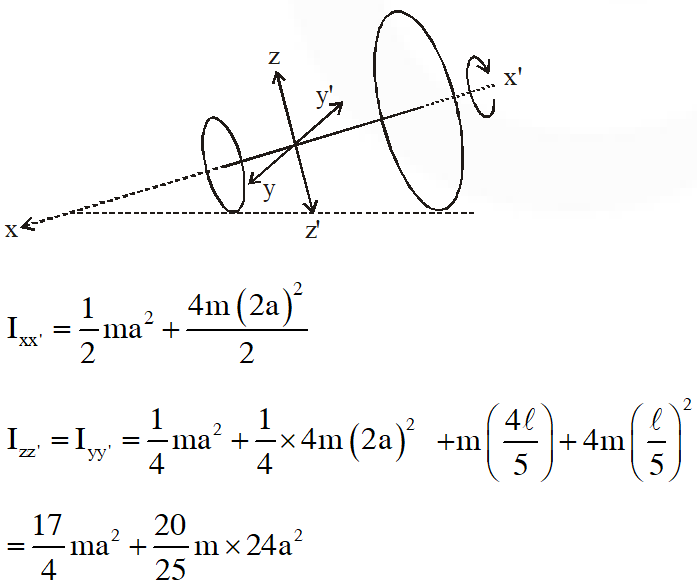
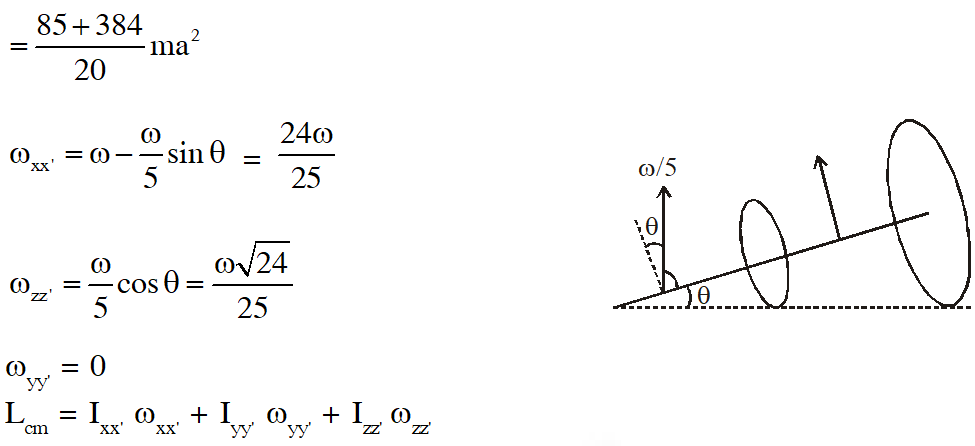
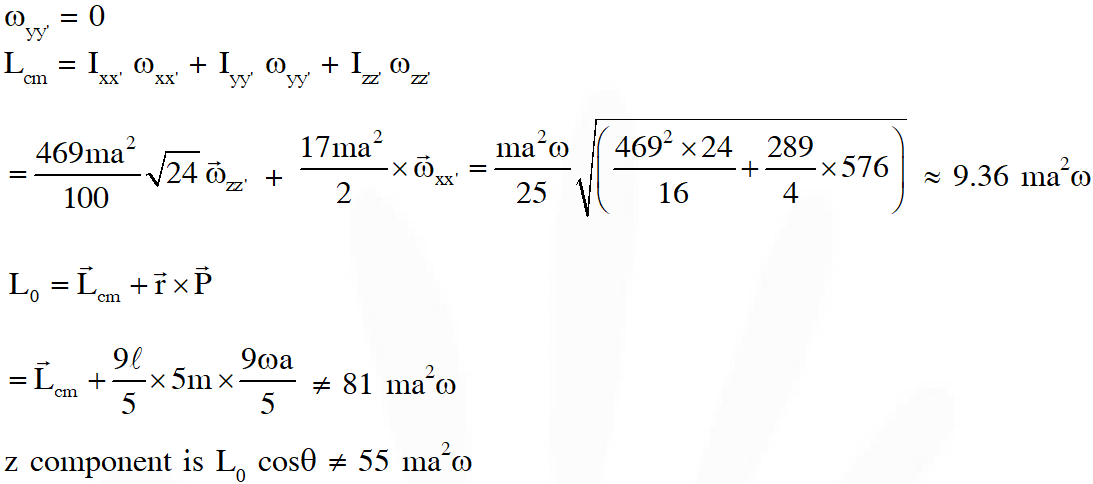
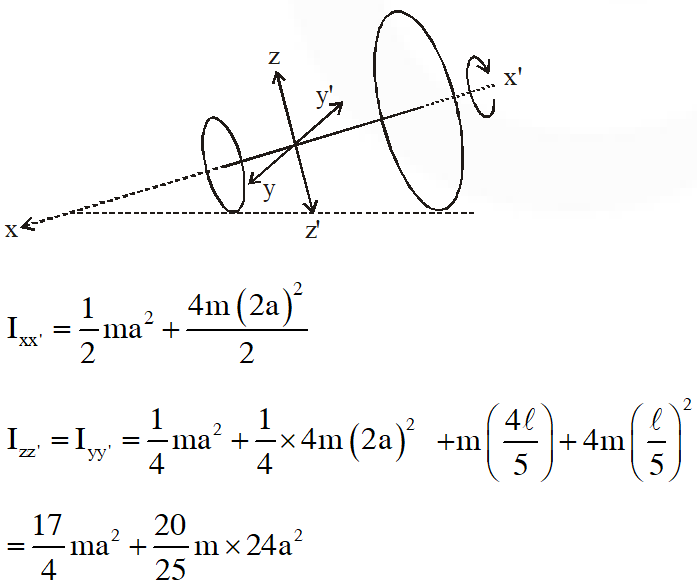
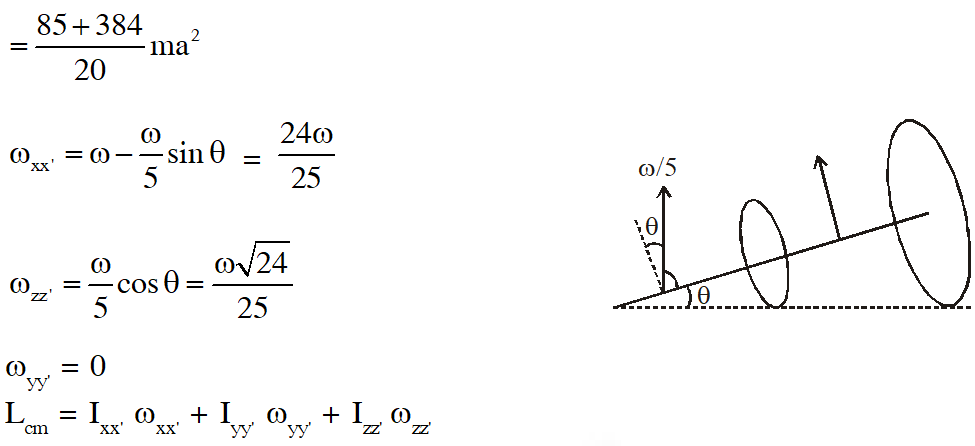
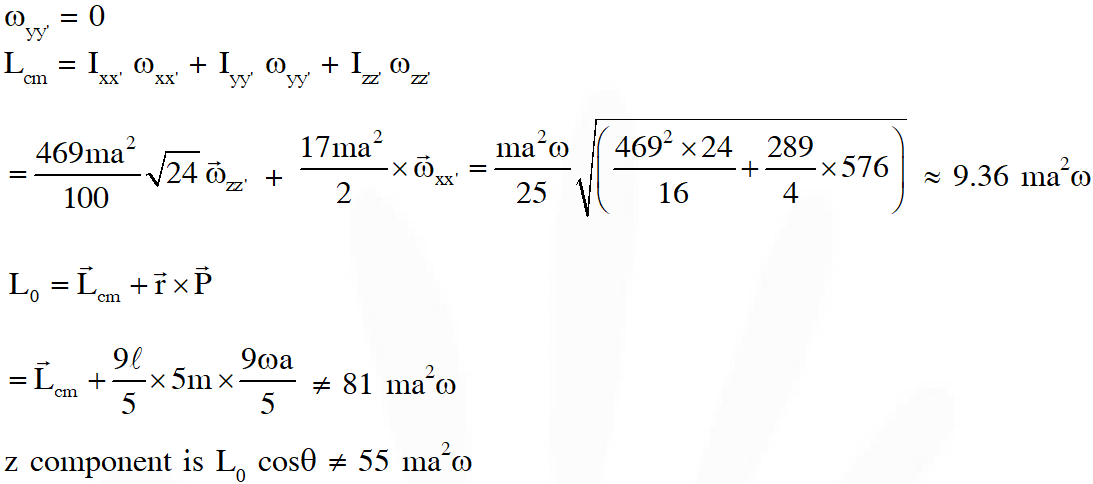

Q. The distance r of the block at time t is :
(A) $\frac{\mathrm{R}}{4}\left(\mathrm{e}^{2 \omega \mathrm{t}}+\mathrm{e}^{-2 \omega \mathrm{t}}\right)$
(B) $\frac{\mathrm{R}}{2} \cos 2 \omega \mathrm{t}$
(C) $\frac{\mathrm{R}}{2} \mathrm{cos} \omega \mathrm{t}$
(D) $\frac{\mathrm{R}}{4}\left(\mathrm{e}^{\mathrm{ot}}+\mathrm{e}^{-\mathrm{ot}}\right)$
[JEE Advanced-2016]
Ans. (D)
Force on block along slot $=m \omega^{2} \mathrm{r}=\mathrm{ma}=\mathrm{m}\left(\frac{\mathrm{vdv}}{\mathrm{dr}}\right)$
$\int_{0}^{\mathrm{v}} \mathrm{vd} \mathrm{v}=\int_{\mathrm{R} / 2}^{\mathrm{r}} \omega^{2} \mathrm{rdr}$
$\frac{\mathrm{v}^{2}}{2}=\frac{\omega^{2}}{2}\left(\mathrm{r}^{2}-\frac{\mathrm{R}^{2}}{4}\right) \Rightarrow \mathrm{v}=\omega \sqrt{\mathrm{r}^{2}-\frac{\mathrm{R}^{2}}{4}}=\frac{\mathrm{dr}}{\mathrm{dt}}$
$\Rightarrow \int_{\mathrm{R} / 4}^{\mathrm{r}} \frac{\mathrm{dr}}{\sqrt{\mathrm{r}^{2}-\frac{\mathrm{R}^{2}}{4}}}=\int_{0}^{\mathrm{t}} \omega \mathrm{dt}$
$\ell_{\mathrm{n}}\left(\frac{\mathrm{r}+\sqrt{\mathrm{r}^{2}-\frac{\mathrm{R}^{2}}{4}}}{\frac{\mathrm{R}}{2}}\right)-\ell \mathrm{n}\left(\frac{\mathrm{R} / 2+\sqrt{\frac{\mathrm{R}^{2}}{4}-\frac{\mathrm{R}^{2}}{4}}}{\frac{\mathrm{R}}{2}}\right)=\omega \mathrm{t}$
$\Rightarrow \mathrm{r}+\sqrt{\mathrm{r}^{2}-\frac{\mathrm{R}^{2}}{4}}=\frac{\mathrm{R}}{2} \mathrm{e}^{\omega \mathrm{t}}$
$\Rightarrow \mathrm{r}^{2}-\frac{\mathrm{R}^{2}}{4}=\frac{\mathrm{R}^{2}}{4} \mathrm{e}^{2 \omega \mathrm{t}}+\mathrm{r}^{2}-2 \mathrm{r} \frac{\mathrm{R}}{2} \mathrm{e}^{\omega \mathrm{t}}$
$\Rightarrow \mathrm{r}=\frac{\frac{\mathrm{R}^{2}}{4} \mathrm{e}^{2 \omega \mathrm{t}}+\frac{\mathrm{R}^{2}}{4}}{\mathrm{Re}^{\mathrm{ot}}}=\frac{\mathrm{R}}{4}\left(\mathrm{e}^{\omega \mathrm{t}}+\mathrm{e}^{-\omega \mathrm{t}}\right)$
Q. The net reaction of the disc on the block is :
(A) $-\mathrm{m\omega}^{2} \mathrm{R}$ cos $\omega$ tì $\hat{\mathrm{j}}-\mathrm{mg} \hat{\mathrm{k}}$
(B) $\mathrm{m\omega}^{2} \mathrm{R} \sin \omega \hat{\mathrm{j}}-\mathrm{mg} \hat{\mathrm{k}}$
(C) $\frac{1}{2} \mathrm{m\omega}^{2} \mathrm{R}\left(\mathrm{e}^{\omega \mathrm{t}}-\mathrm{e}^{-\omega \mathrm{t}}\right) \hat{\mathrm{j}}+\mathrm{mg} \hat{\mathrm{k}}$
(D) $\frac{1}{2} \mathrm{m\omega}^{2} \mathrm{R}\left(\mathrm{e}^{2 \omega \mathrm{t}}-\mathrm{e}^{-2 \omega \mathrm{t}}\right) \hat{\mathrm{j}}+\mathrm{mg} \hat{\mathrm{k}}$
[JEE Advanced-2016]
Ans. (C)
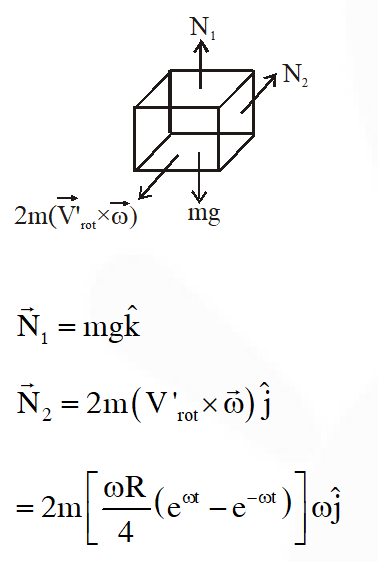
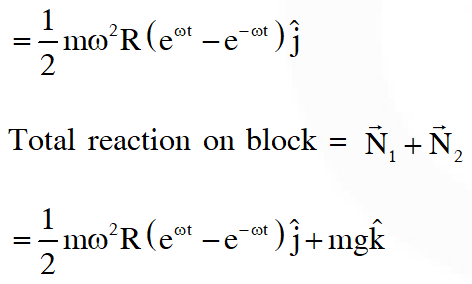
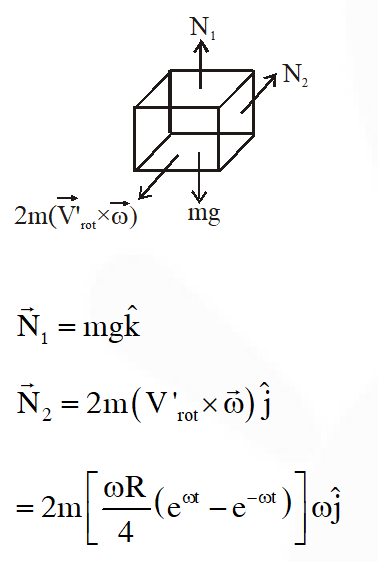
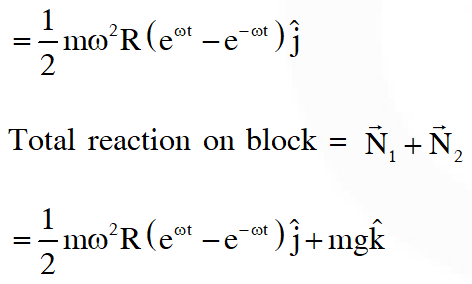
Q. A rigid uniform bar AB of length L is slipping from its vertical position on a frictionless floor (as shown in the figure). At some instant of time, the angle made by the bar with the vertical is $\theta$. Which of the following statements about its motion is/are correct ? 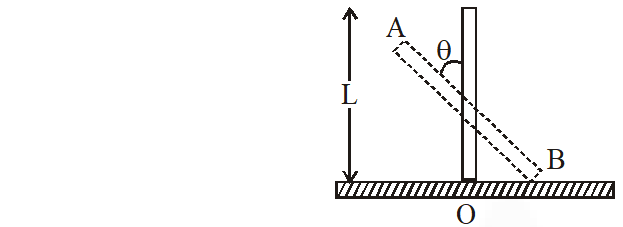 (A) When the bar makes an angle $\theta$ with the vertical, the displacement of its midpoint from the initial position is proportional to $(1-\cos \theta)$
(B) The midpoint of the bar will fall vertically downward
(C) Instantaneous torque about the point in contact with the floor is proportional to $\sin \theta$
(D) The trajectory of the point $A$ is a parabola
[JEE Advanced-2017]
(A) When the bar makes an angle $\theta$ with the vertical, the displacement of its midpoint from the initial position is proportional to $(1-\cos \theta)$
(B) The midpoint of the bar will fall vertically downward
(C) Instantaneous torque about the point in contact with the floor is proportional to $\sin \theta$
(D) The trajectory of the point $A$ is a parabola
[JEE Advanced-2017]
 (A) When the bar makes an angle $\theta$ with the vertical, the displacement of its midpoint from the initial position is proportional to $(1-\cos \theta)$
(B) The midpoint of the bar will fall vertically downward
(C) Instantaneous torque about the point in contact with the floor is proportional to $\sin \theta$
(D) The trajectory of the point $A$ is a parabola
[JEE Advanced-2017]
(A) When the bar makes an angle $\theta$ with the vertical, the displacement of its midpoint from the initial position is proportional to $(1-\cos \theta)$
(B) The midpoint of the bar will fall vertically downward
(C) Instantaneous torque about the point in contact with the floor is proportional to $\sin \theta$
(D) The trajectory of the point $A$ is a parabola
[JEE Advanced-2017]
Ans. (A,B,C)
When the bar makes an angle $\theta ;$ the height of its COM (mid point) is $\frac{\mathrm{L}}{2} \cos \theta$
$\therefore$ displacement $=\mathrm{L}-\frac{\mathrm{L}}{2} \cos \theta=\frac{\mathrm{L}}{2}(1-\cos \theta)$
Since force on COM is only along the vertical direction, hence COM is falling vertically downward.
Instantaneous torque about point of contact is
$\mathrm{Mg} \times \frac{\mathrm{L}}{2} \sin \theta$
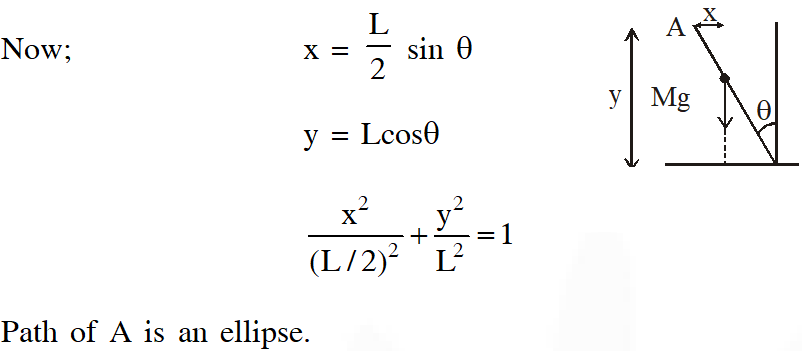
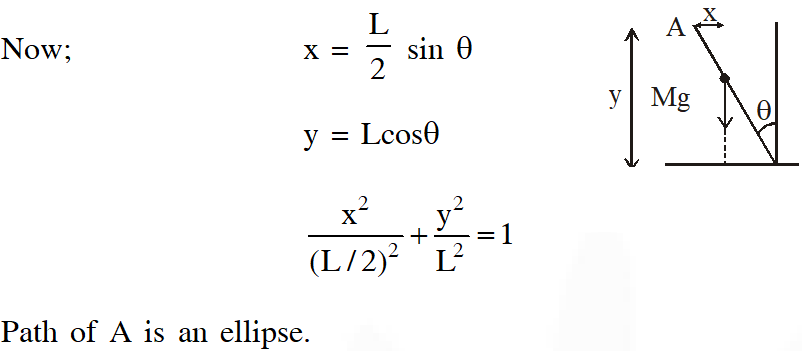
Q. A wheel of radius R and mass M is placed at the bottom of a fixed step of height R as shown in the figure. A constant force is continuously applied on the surface of the wheel so that it just climbs the step without slipping. Consider the torque about an axis normal to the plane of the paper passing through the point Q. Which of the following options is/are correct ?
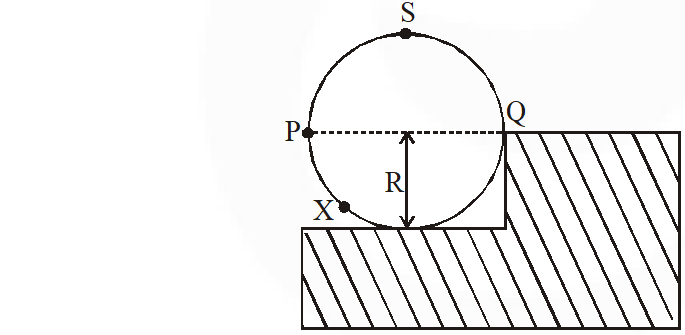 (A) If the force is applied normal to the circumference at point X then $\tau$ is constant
(B) If the force is applied tangentially at point S then $\tau \neq 0$ but the wheel never climbs the step
(C) If the force is applied normal to the circumference at point P then $\tau$ is zero
(D) If the force is applied at point P tangentially then t decreases continuously as the wheel climbs
[JEE Advanced-2017]
(A) If the force is applied normal to the circumference at point X then $\tau$ is constant
(B) If the force is applied tangentially at point S then $\tau \neq 0$ but the wheel never climbs the step
(C) If the force is applied normal to the circumference at point P then $\tau$ is zero
(D) If the force is applied at point P tangentially then t decreases continuously as the wheel climbs
[JEE Advanced-2017]
 (A) If the force is applied normal to the circumference at point X then $\tau$ is constant
(B) If the force is applied tangentially at point S then $\tau \neq 0$ but the wheel never climbs the step
(C) If the force is applied normal to the circumference at point P then $\tau$ is zero
(D) If the force is applied at point P tangentially then t decreases continuously as the wheel climbs
[JEE Advanced-2017]
(A) If the force is applied normal to the circumference at point X then $\tau$ is constant
(B) If the force is applied tangentially at point S then $\tau \neq 0$ but the wheel never climbs the step
(C) If the force is applied normal to the circumference at point P then $\tau$ is zero
(D) If the force is applied at point P tangentially then t decreases continuously as the wheel climbs
[JEE Advanced-2017]
Ans. (C)
(A) is incorrect.

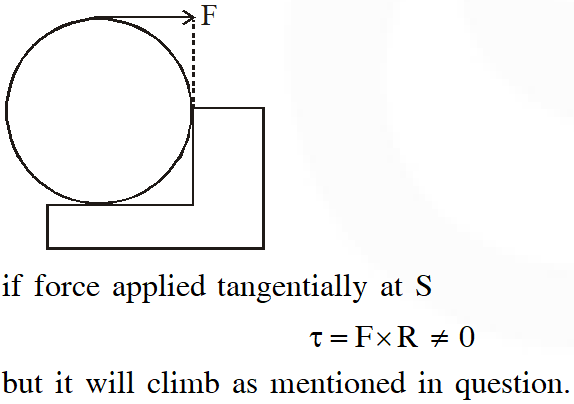
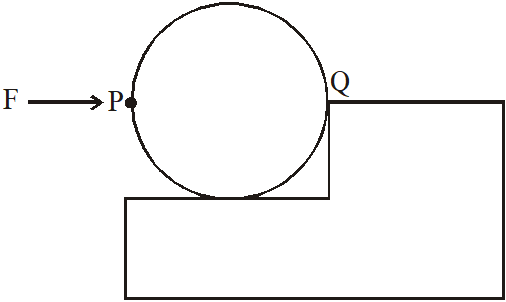 if force is applied at P tangentially the
$\tau=\mathrm{F} \times 2 \mathrm{R}=\mathrm{constant}$
if force is applied at P tangentially the
$\tau=\mathrm{F} \times 2 \mathrm{R}=\mathrm{constant}$

 if force is applied at P tangentially the
$\tau=\mathrm{F} \times 2 \mathrm{R}=\mathrm{constant}$
if force is applied at P tangentially the
$\tau=\mathrm{F} \times 2 \mathrm{R}=\mathrm{constant}$

Q. The total kinetic energy of the ring is :-
(A) $\mathrm{M} \omega_{0}^{2} \mathrm{R}^{2}$
(B) $\operatorname{Mo}_{0}^{2}(\mathrm{R}-\mathrm{r})^{2}$
(C) $\frac{1}{2} \mathrm{M} \omega_{0}^{2}(\mathrm{R}-\mathrm{r})^{2}$
(D) $\frac{3}{2} \mathrm{M} \omega_{0}^{2}(\mathrm{R}-\mathrm{r})^{2}$
[JEE Advanced-2017]
Ans. Bonus
Q. The minimum value of $\omega_{0}$ below which the ring will drop down is :-
(A) $\sqrt{\frac{3 \mathrm{g}}{2 \mu(\mathrm{R}-\mathrm{r})}}$
(B) $\sqrt{\frac{\mathrm{g}}{\mu(\mathrm{R}-\mathrm{r})}}$
(C) $\sqrt{\frac{2 \mathrm{g}}{\mu(\mathrm{R}-\mathrm{r})}}$
(D) $\sqrt{\frac{\mathrm{g}}{2 \mu(\mathrm{R}-\mathrm{r})}}$
[JEE Advanced-2017]
Ans. (B)
$\mu \mathrm{M} \omega_{0}^{2}(\mathrm{R}-\mathrm{r})=\mathrm{Mg}$
$\omega_{0}=\sqrt{\frac{\mathrm{g}}{\mu(\mathrm{R}-\mathrm{r})}}$
Q. The potential energy of a particle of mass m at a distance r from a fixed point O is given by $\mathrm{V}(\mathrm{r})=\mathrm{kr}^{2} / 2$, where k is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius R about the point O. If v is the speed of the particle and L is the magnitude of its angular momentum about O, which of the following statements is (are) true ?
(A) $v=\sqrt{\frac{\mathrm{k}}{2 \mathrm{m}}} \mathrm{R}$
(B) $v=\sqrt{\frac{k}{m}} R$
(C) $\mathrm{L}=\sqrt{\mathrm{mk}} \mathrm{R}^{2}$
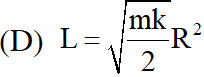 [JEE Advanced-2018]
[JEE Advanced-2018]
Ans. (B,C)
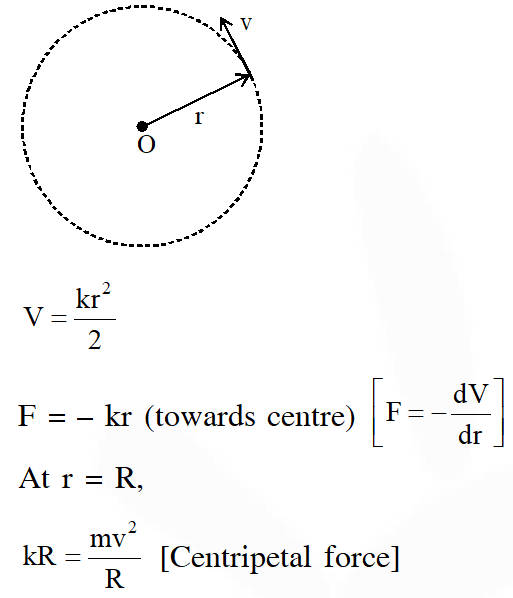
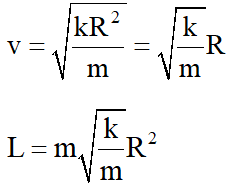
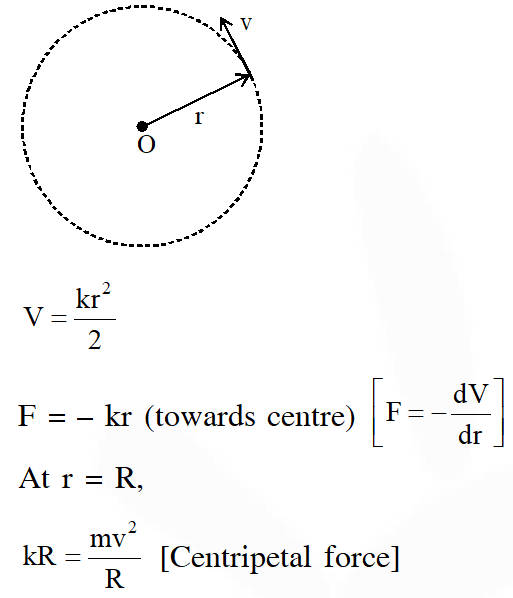
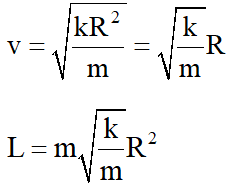
Q. Consider a body of mass $1.0 \mathrm{kg}$ at rest at the origin at time $\mathrm{t}=0 .$ A force $\overrightarrow{\mathrm{F}}=(\alpha \mathrm{ti}+\beta \hat{\mathrm{j}})$ is
applied on the body, where $\alpha=1.0 \mathrm{Ns}^{-1}$ and $\beta=1.0 \mathrm{N}$. The torque acting on the body about
the origin at time $\mathrm{t}=1.0 \mathrm{s}$ is $\vec{\tau} .$ Which of the following statements is (are) true?
(A) $|\vec{\tau}|=\frac{1}{3} \mathrm{Nm}$
(B) The torque $\vec{\tau}$ is in the direction of the unit vector $+\hat{\mathrm{k}}$
(C) The velocity of the body at $\mathrm{t}=1 \mathrm{s}$ is $\overrightarrow{\mathrm{v}}=\frac{1}{2}(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}) \mathrm{ms}^{-1}$
(D) The magnitude of displacement of the body at $t=1$ s is $\frac{1}{6} m$
[JEE Advanced-2018]
Ans. (A,C)
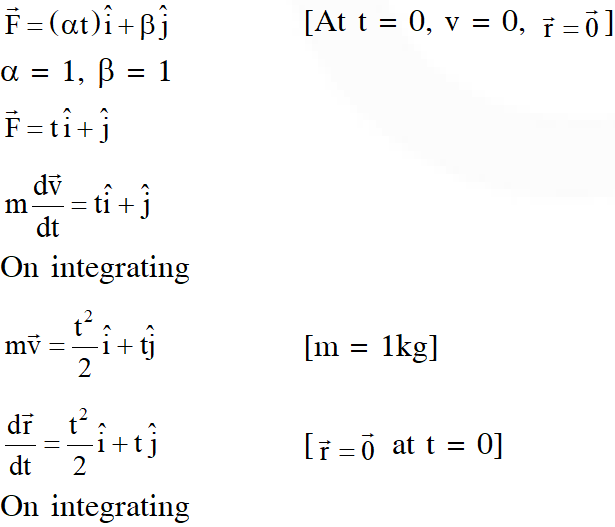
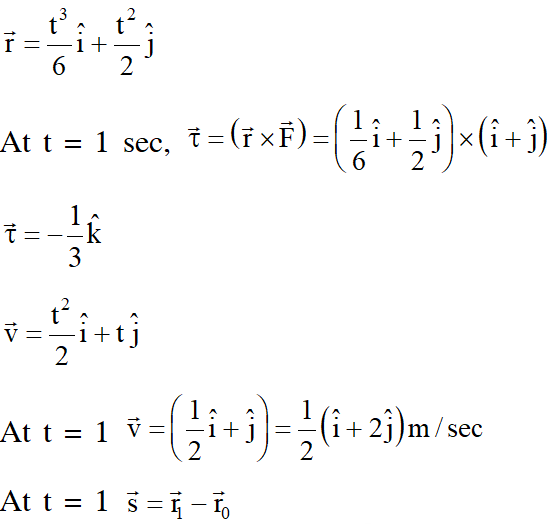
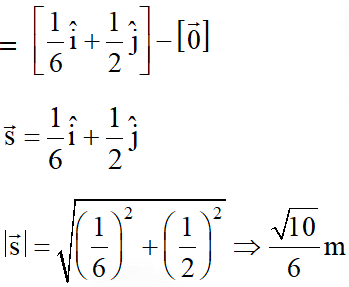
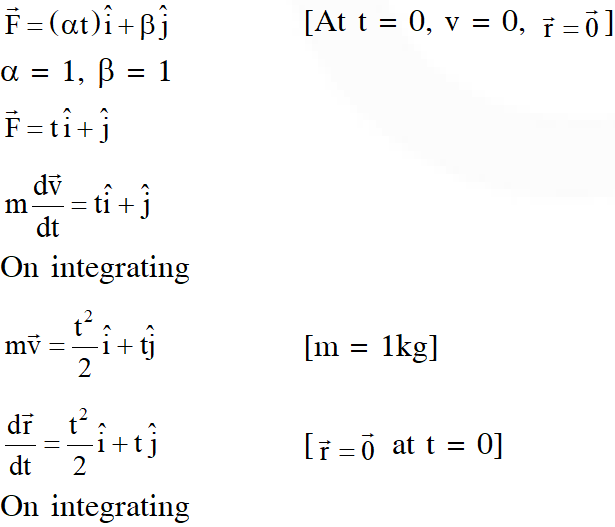
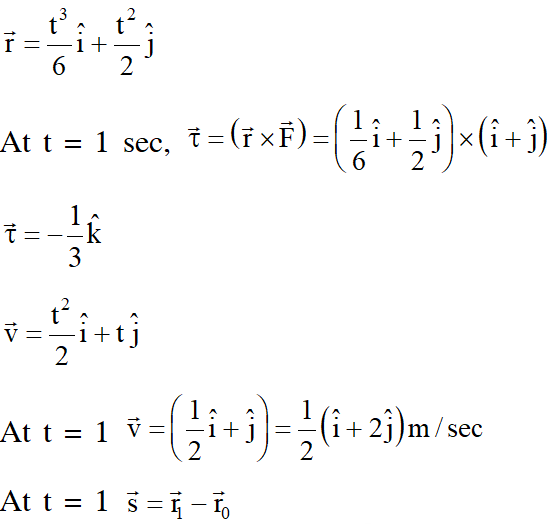
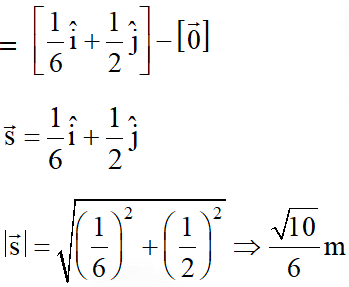
Q. A ring and a disc are initially at rest, side by side, at the top of an inclined plane which makes an angle 60° with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is $(2-\sqrt{3}) / \sqrt{10} \mathrm{s}$, then the height of the top of the inclined plane, in meters, is _____. Take g = 10 $\mathrm{ms}^{-2}$.
[JEE Advanced-2018]
Ans. 0.75
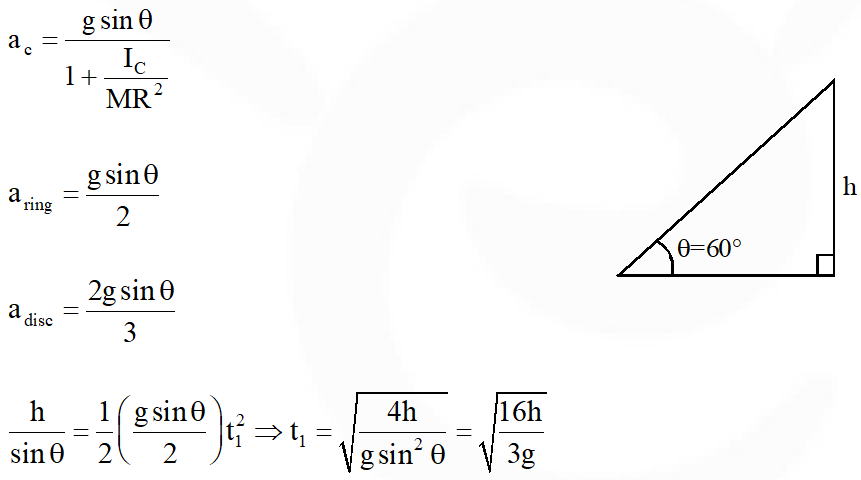
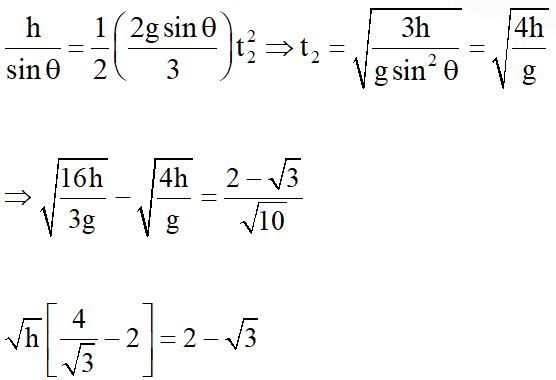
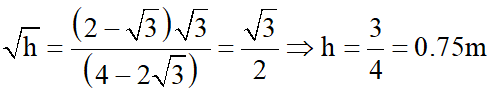
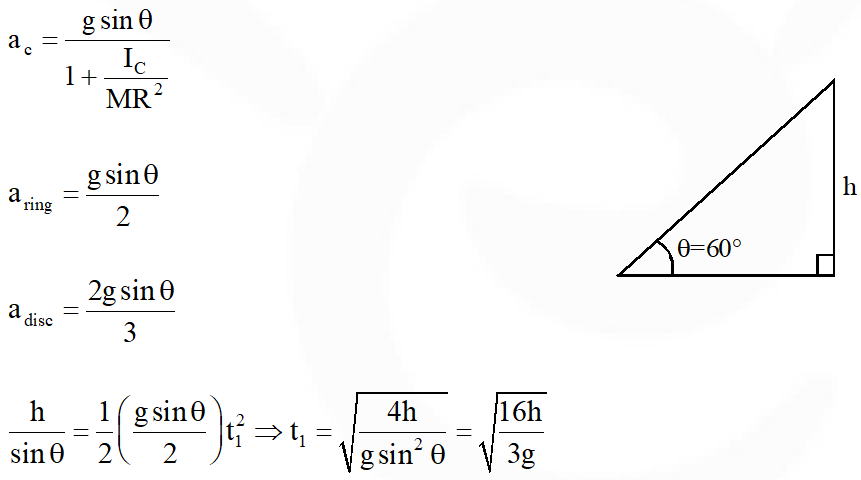
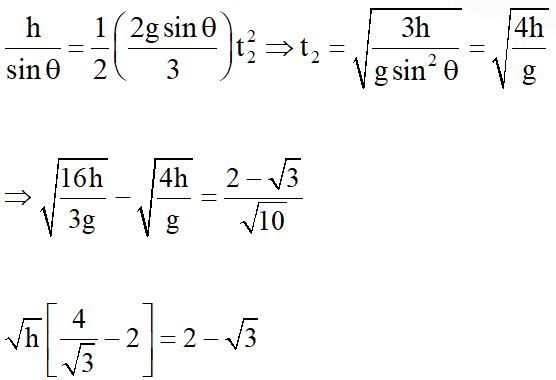
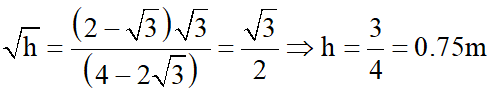
Q. In the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List–II, five physical quantities of the particle are mentioned; $\overrightarrow{\mathrm{p}}$ is the linear momentum $\overrightarrow{\mathrm{L}}$ is the angular momentum about the origin, K is the kinetic energy, U is the potential energy and E is the total energy. Match each path in List–I with those quantities in List–II, which are conserved for that path
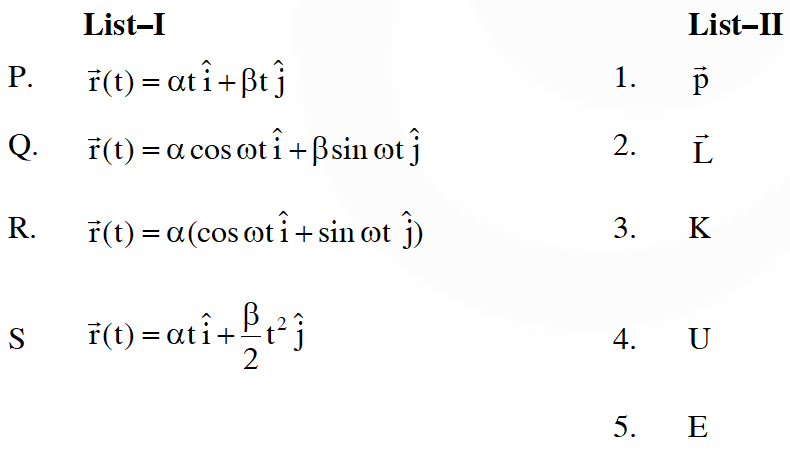
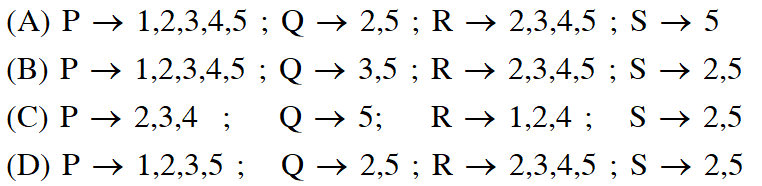 [JEE Advanced-2018]
[JEE Advanced-2018]
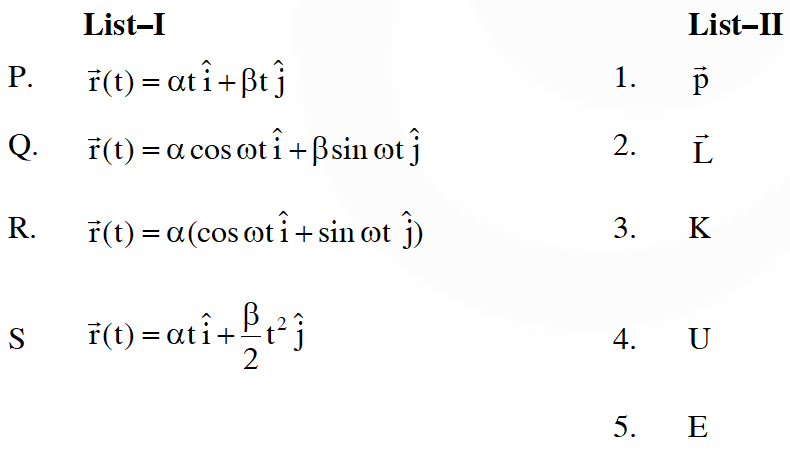
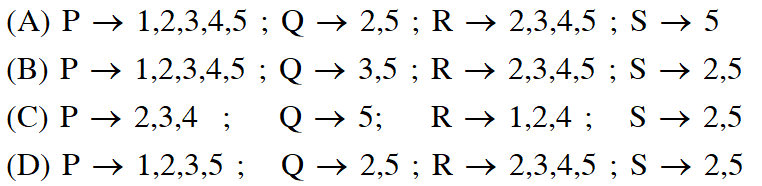 [JEE Advanced-2018]
[JEE Advanced-2018]
Ans. (A)
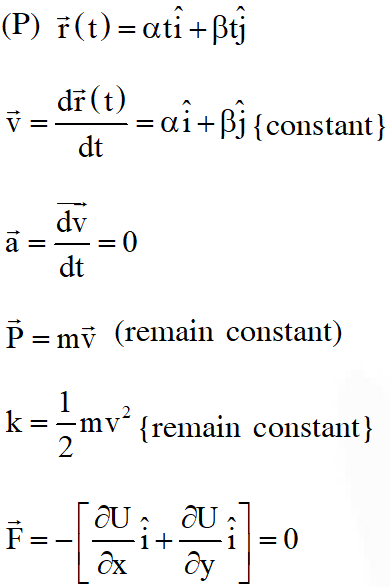
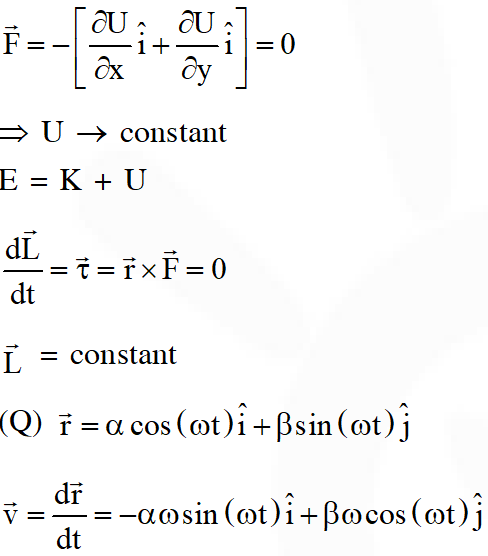
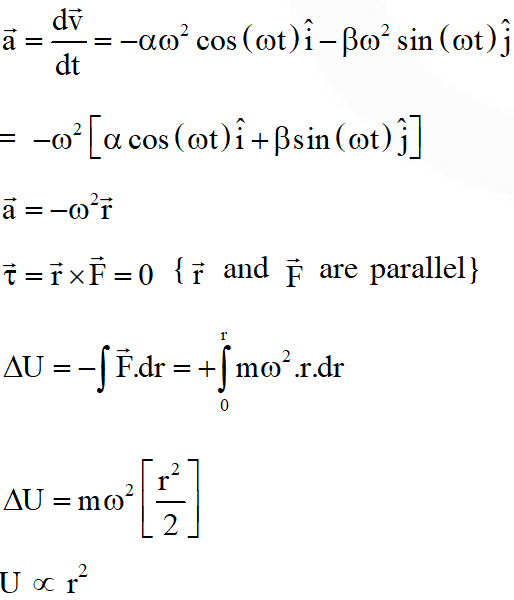
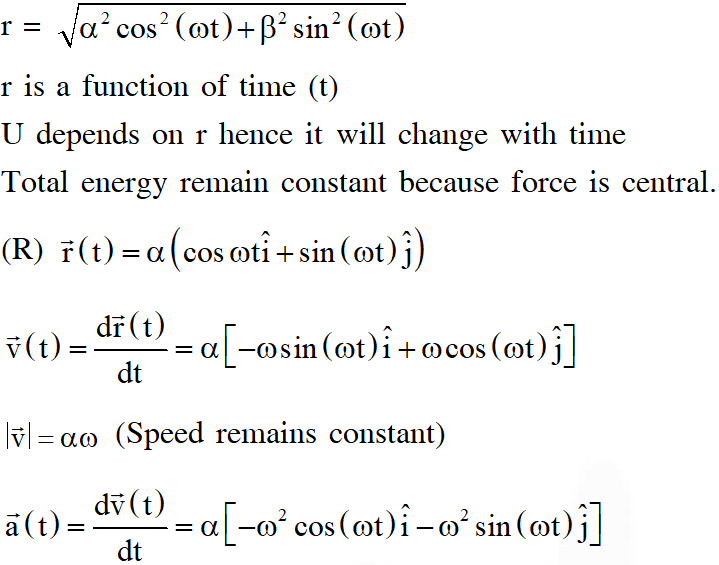

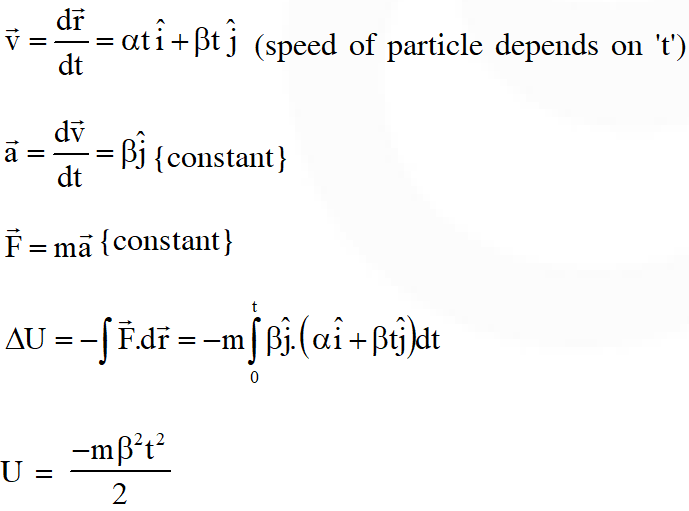
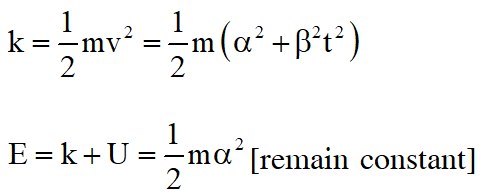
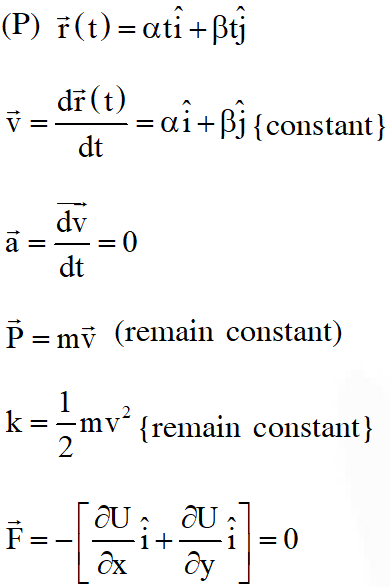
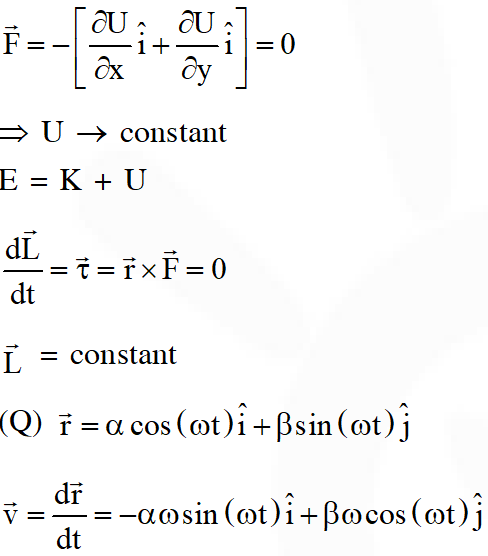
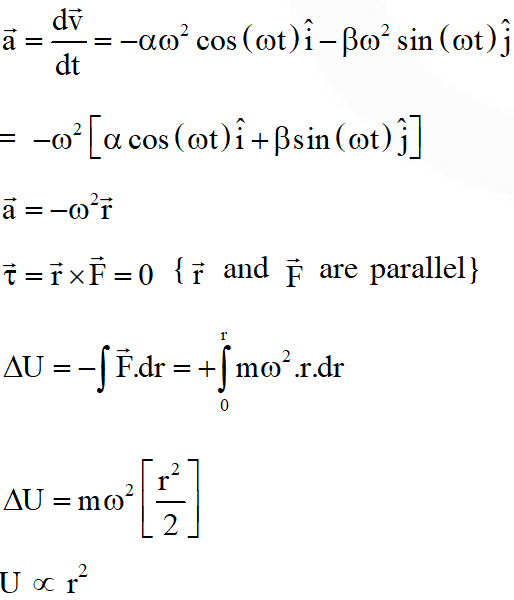
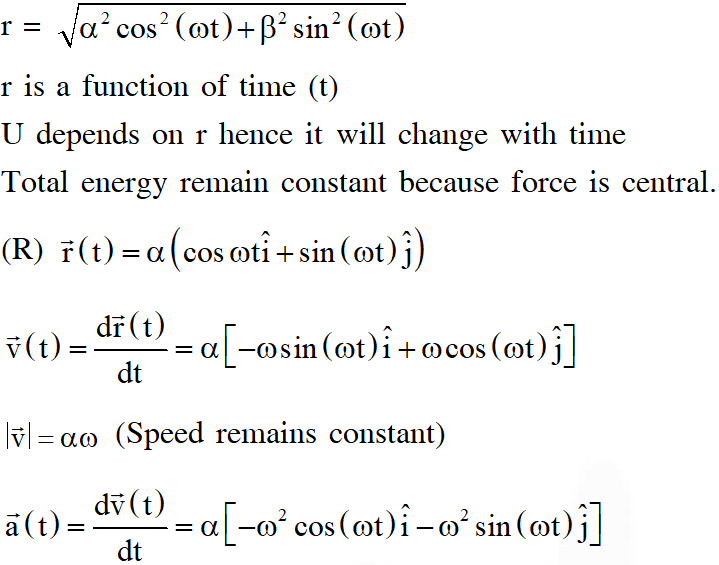

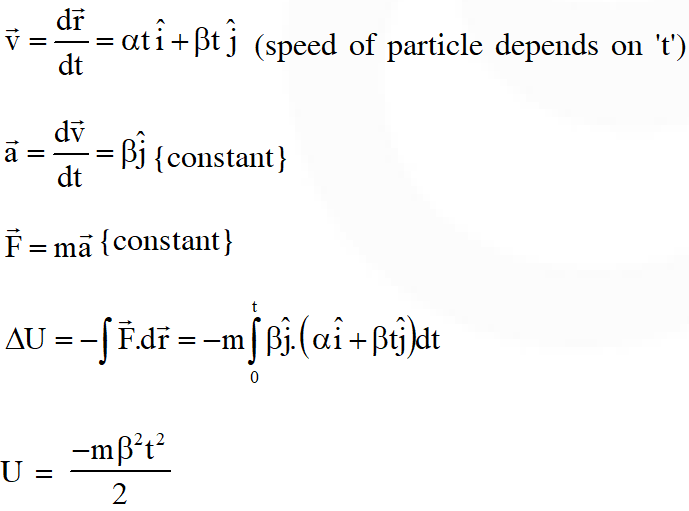
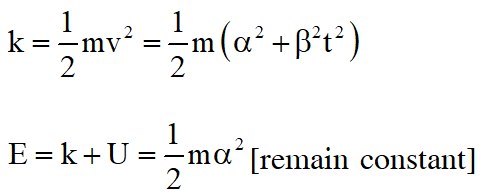
Comments
Elon Musk
July 31, 2021, 4:40 p.m.
sir in question iitjee 2011 wrong diagram is showen very confusinf
Kartikeya
May 7, 2021, 12:50 p.m.
Very useful but please try to display the options line by line so that it more comfortable
abhishek mangal
Dec. 14, 2020, 1:01 p.m.
this is message for all esaral team thankyou so much for providing us jee mains and advance previous years question
