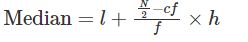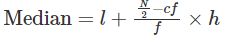Statistics For Class 10th

Statistics for class 10th students -Welcome to the world of statistics! As a student in 10th grade, you may be wondering why statistics is even relevant to your studies. The truth is, statistics is an essential branch of mathematics that helps us make sense of the world around us. By analyzing data and drawing conclusions, we can better understand patterns and trends in everything from social issues to scientific experiments. In this article, we will explore the fundamentals of statistics for class 10th students, including concepts such as mean, median, and mode, as well as how to represent data using graphs and charts. So, let's dive in and explore the exciting world of statistics!

Answers to Maths NCERT Class 10 Chapter 14 – Statistics

Exercise 14.1 Page: 270 - Statistics for class 10th students

1. A survey was conducted by a group of students as a part of their environment awareness program, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

Which method did you use for finding the mean, and why?

Solution:

To find the mean value, we will use the direct method because the numerical value of f_i and x_i are small.

Find the midpoint of the given interval using the formula.

Midpoint (x_i) = (upper limit + lower limit)/2

The formula to find the mean is:

Mean = x̄ = ∑f_i x_i /∑f_i

= 162/20

= 8.1

Therefore, the mean number of plants per house is 8.1. - Statistics for class 10th students

2. Consider the following distribution of daily wages of 50 workers of a factory.

Find the mean daily wages of the workers of the factory by using an appropriate method.

Solution:

Find the midpoint of the given interval using the formula.

Midpoint (x_i) = (upper limit + lower limit)/2

In this case, the value of mid-point (x_i) is very large, so let us assume the mean value, a = 550.

Class interval (h) = 20

So, u_i = (x_i – a)/h

u_i = (x_i – 550)/20

Substitute and find the values as follows:

So, the formula to find out the mean is:

Mean = x̄ = a + h(∑f_iu_i /∑f_i ) = 550 + [20 × (-12/50)] = 550 – 4.8 = 545.20

Thus, mean daily wage of the workers = Rs. 545.20

3. The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f. -Statistics for class 10th students

Solution:

To find out the missing frequency, use the mean formula.

Given, mean x̄ = 18

The mean formula is

Mean = x̄ = ∑f_ix_i /∑f_i = (752 + 20f)/ (44 + f)

Now substitute the values and equate to find the missing frequency (f)

⇒ 18 = (752 + 20f)/ (44 + f)

⇒ 18(44 + f) = (752 + 20f)

⇒ 792 + 18f = 752 + 20f

⇒ 792 + 18f = 752 + 20f

⇒ 792 – 752 = 20f – 18f

⇒ 40 = 2f

⇒ f = 20

So, the missing frequency, f = 20.

4. Thirty women were examined in a hospital by a doctor, and the number of heartbeats per minute were recorded and summarised as follows. Find the mean heartbeats per minute for these women, choosing a suitable method.

Solution:

From the given data, let us assume the mean as a = 75.5

x_i = (Upper limit + Lower limit)/2

Class size (h) = 3

Now, find the u_i and f_iu_i as follows:

Mean = x̄ = a + h(∑f_iu_i /∑f_i )

= 75.5 + 3 × (4/30)

= 75.5 + (4/10)

= 75.5 + 0.4

= 75.9

Therefore, the mean heart beats per minute for these women is 75.9

5. In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose? -Statistics for class 10th students

Solution:

The given data is not continuous, so we add 0.5 to the upper limit and subtract 0.5 from the lower limit as the gap between two intervals is 1.

Here, assumed mean (a) = 57

Class size (h) = 3

Here, the step deviation is used because the frequency values are big.

The formula to find out the Mean is:

Mean = x̄ = a + h(∑f_iu_i /∑f_i )

= 57 + 3(25/400)

= 57 + 0.1875

= 57.19

Therefore, the mean number of mangoes kept in a packing box is 57.19

6. The table below shows the daily expenditure on food of 25 households in a locality.

Find the mean daily expenditure on food by a suitable method.

Solution:

Find the midpoint of the given interval using the formula.

Midpoint (x_i) = (upper limit + lower limit)/2

Let us assume the mean (a) = 225

Class size (h) = 50

Mean = x̄ = a + h(∑f_iu_i /∑f_i )

= 225 + 50(-7/25)

= 225 – 14

= 211

Therefore, the mean daily expenditure on food is 211.

7. To find out the concentration of SO₂ in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below:

Find the mean concentration of SO₂ in the air.

Solution:

To find out the mean, first find the midpoint of the given frequencies as follows:

The formula to find out the mean is

Mean = x̄ = ∑f_ix_i /∑f_i

= 2.96/30

= 0.099 ppm

Therefore, the mean concentration of SO₂ in the air is 0.099 ppm. - Statistics for class 10th students

8. A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

Solution:

Find the midpoint of the given interval using the formula.

Midpoint (x_i) = (upper limit + lower limit)/2

The mean formula is,

Mean = x̄ = ∑f_ix_i /∑f_i

= 499/40

= 12.48 days

Therefore, the mean number of days a student was absent = 12.48.

9. The following table gives the literacy rate (in percentage) of 35 cities. Find the mean

literacy rate.

Solution:

Find the midpoint of the given interval using the formula.

Midpoint (x_i) = (upper limit + lower limit)/2

In this case, the value of mid-point (x_i) is very large, so let us assume the mean value, a = 70.

Class interval (h) = 10

So, u_i = (x_i – a)/h

u_i = (x_i – 70)/10

Substitute and find the values as follows:

So, Mean = x̄ = a + (∑f_iu_i /∑f_i) × h

= 70 + (-2/35) × 10

= 69.43

Therefore, the mean literacy part = 69.43%

Exercise 14.2 Page: 275

1. The following table shows the ages of the patients admitted to a hospital during a year:

Find the mode and the mean of the data given above. Compare and interpret the two

measures of central tendency. - Statistics for class 10th students

Solution:

To find out the modal class, let us the consider the class interval with high frequency.

Here, the greatest frequency = 23, so the modal class = 35 – 45,

Lower limit of modal class = l = 35,

class width (h) = 10,

f_m = 23,

f₁ = 21 and f₂ = 14

The formula to find the mode is

Mode = l + [(f_m – f₁)/ (2f_m – f₁ – f₂)] × h

Substitute the values in the formula, we get

Mode = 35+[(23-21)/(46-21-14)]×10

= 35 + (20/11)

= 35 + 1.8

= 36.8 years

So the mode of the given data = 36.8 years

Calculation of Mean:

First find the midpoint using the formula, x_i = (upper limit +lower limit)/2

The mean formula is

Mean = x̄ = ∑f_ix_i /∑f_i

= 2830/80

= 35.375 years

Therefore, the mean of the given data = 35.375 years

2. The following data gives the information on the observed lifetimes (in hours) of 225

electrical components:

Determine the modal lifetimes of the components. - Statistics for class 10th students

Solution:

From the given data the modal class is 60–80.

Lower limit of modal class = l = 60,

The frequencies are:

f_m = 61, f₁ = 52, f₂ = 38 and h = 20

The formula to find the mode is

Mode = l+ [(f_m – f₁)/(2f_m – f₁ – f₂)] × h

Substitute the values in the formula, we get

Mode = 60 + [(61 – 52)/ (122 – 52 – 38)] × 20

Mode = 60 + [(9 × 20)/32]

Mode = 60 + (45/8) = 60 + 5.625

Therefore, modal lifetime of the components = 65.625 hours.

3. The following data gives the distribution of total monthly household expenditure of 200

families of a village. Find the modal monthly expenditure of the families. Also, find the

mean monthly expenditure:

Solution:

Given data:

Modal class = 1500-2000,

l = 1500,

Frequencies:

f_m = 40 f₁ = 24, f₂ = 33 and

h = 500

Mode formula:

Mode = l + [(f_m – f₁)/ (2f_m – f₁ – f₂)] × h

Substitute the values in the formula, we get

Mode = 1500 + [(40 – 24)/ (80 – 24 – 33)] × 500

Mode = 1500 + [(16 × 500)/23]

Mode = 1500 + (8000/23) = 1500 + 347.83

Therefore, modal monthly expenditure of the families = Rupees 1847.83

Calculation for mean:

First find the midpoint using the formula, x_i =(upper limit +lower limit)/2

Let us assume a mean, (a) be 2750.

The formula to calculate the mean,

Mean = x̄ = a +(∑f_iu_i /∑f_i) × h

Substitute the values in the given formula

= 2750 + (-35/200) × 500

= 2750 – 87.50

= 2662.50

So, the mean monthly expenditure of the families = Rs. 2662.50

4. The following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures - Statistics for class 10th students

Solution:

Given data:

Modal class = 30 – 35,

l = 30,

Class width (h) = 5,

f_m = 10, f₁ = 9 and f₂ = 3

Mode Formula:

Mode = l + [(f_m – f₁)/ (2f_m – f₁ – f₂)] × h

Substitute the values in the given formula

Mode = 30 + [(10 – 9)/ (20 – 9 – 3)] × 5

= 30 + (5/8)

= 30 + 0.625

= 30.625

Therefore, the mode of the given data = 30.625

Calculation of mean:

Find the midpoint using the formula, x_i =(upper limit +lower limit)/2

Mean = x̄ = ∑f_ix_i /∑f_i

= 1022.5/35

= 29.2 (approx)

Therefore, mean = 29.2 - Statistics for class 10th students

5. The given distribution shows the number of runs scored by some top batsmen of the world in one- day international cricket matches.

Find the mode of the data.

Solution:

Given data:

Modal class = 4000 – 5000,

l = 4000,

class width (h) = 1000,

f_m = 18, f₁ = 4 and f₂ = 9

Mode Formula:

Mode = l + [(f_m – f₁)/ (2f_m – f₁ – f₂)] × h

Substitute the values

Mode = 4000 + [(18 – 4)/ (36 – 4 – 9)] × 1000

= 4000 + (14000/23)

= 4000 + 608.695

= 4608.695

= 4608.7 (approximately)

Thus, the mode of the given data is 4608.7 runs.

6. A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarized it in the table given below. Find the mode of the data:

Solution:

Given Data:

Modal class = 40 – 50, l = 40,

Class width (h) = 10, f_m = 20, f₁ = 12 and f₂ = 11

Mode = l + [(f_m – f₁)/(2f_m – f₁ – f₂)] × h

Substitute the values

Mode = 40 + [(20 – 12)/ (40 – 12 – 11)] × 10

= 40 + (80/17)

= 40 + 4.7

= 44.7

Thus, the mode of the given data is 44.7 cars.

Exercise 14.3 Page: 287

1. The following frequency distribution gives the monthly consumption of an electricity of 68 consumers in a locality. Find the median, mean and mode of the data and compare them.

Solution:

Find the cumulative frequency of the given data as follows:

From the table, it is observed that, N = 68 and hence N/2=34

Hence, the median class is 125-145 with cumulative frequency = 42

Where, l = 125, N = 68, cf = 22, f = 20, h = 20

Median is calculated as follows:

= 125 + [(34 − 22)/20] × 20

= 125 + 12

= 137

Therefore, median = 137

To calculate the mode:

Modal class = 125-145,

f_m or f₁ = 20, f₀ = 13, f₂ = 14 & h = 20

Mode formula:

Mode = l+ [(f₁ – f₀)/(2f₁ – f₀ – f₂)] × h

Mode = 125 + [(20 – 13)/ (40 – 13 – 14)] × 20

= 125 + (140/13)

= 125 + 10.77

= 135.77

Therefore, mode = 135.77

Calculate the Mean:

x̄ = a + h (∑f_iu_i/∑f_i) = 135 + 20 (7/68)

Mean = 137.05

In this case, mean, median and mode are more/less equal in this distribution.

2. If the median of a distribution given below is 28.5, find the value of x & y.

Solution:

Given data, n = 60

Median of the given data = 28.5

Where, N/2 = 30

Median class is 20 – 30 with a cumulative frequency = 25 + x

Lower limit of median class, l = 20,

cf = 5 + x,

f = 20 & h = 10

Substitute the values

28.5 = 20 + [(30 − 5 − x)/20] × 10

8.5 = (25 – x)/2

17 = 25 – x

Therefore, x = 8.

Now, from cumulative frequency, we can identify the value of x + y as follows:

Since,

60 = 45 + x + y

Now, substitute the value of x, to find y

60 = 45 + 8 + y

y = 60 – 53

y = 7

Therefore, the value of x = 8 and y = 7.

3. The life insurance agent found the following data for the distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to the persons whose age is 18 years onwards but less than the 60 years. - Statistics for class 10th students

Solution:

Given data: N = 100 and N/2 = 50

Median class = 35-40

Then, l = 35, cf = 45, f = 33 & h = 5

Median = 35 + [(50 – 45)/33] × 5

= 35 + (25/33)

= 35.76

Therefore, the median age = 35.76 years.

4. The lengths of 40 leaves in a plant are measured correctly to the nearest millimeter, and the data obtained is represented as in the following table: - Statistics for class 10th students

Find the median length of the leaves.

(Hint : The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 – 126.5, 126.5 – 135.5, . . ., 171.5 – 180.5.)

Solution:

Since the data are not continuous reduce 0.5 in the lower limit and add 0.5 in the upper limit.

So, the data obtained are:

N = 40 and N/2 = 20

Median class = 144.5-153.5

then, l = 144.5,

cf = 17, f = 12 & h = 9

Median = 144.5 + [(20 – 17)/ 12] × 9

= 144.5 + (9/4)

= 146.75 mm

Therefore, the median length of the leaves = 146.75 mm.

5. The following table gives the distribution of a lifetime of 400 neon lamps.

Find the median lifetime of a lamp.

Solution:

Data:

N = 400 & N/2 = 200

Median class = 3000 – 3500

Therefore, l = 3000, cf = 130,

f = 86 & h = 500

Median = 3000 + [(200 – 130)/86] × 500

= 3000 + (35000/86)

= 3000 + 406.98

= 3406.98

Therefore, the median lifetime of the lamps = 3406.98 hours

6. 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, find the modal size of the surnames. - Statistics for class 10th students

Solution:

To calculate median:

Given:

N = 100 & N/2 = 50

Median class = 7-10

Therefore, l = 7, cf = 36, f = 40 & h = 3

Median = 7 + [(50 – 36)/40] × 3

Median = 7 + (42/40)

Median = 8.05

Calculate the Mode:

Modal class = 7-10,

Where, l = 7, f₁ = 40, f₀ = 30, f₂ = 16 & h = 3

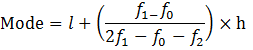
Mode = 7 + [(40 – 30)/(2 × 40 – 30 – 16)] × 3

= 7 + (30/34)

= 7.88

Therefore mode = 7.88

Calculate the Mean:

Mean = x̄ = ∑f_i x_i /∑f_i

Mean = 832/100 = 8.32

Therefore, mean = 8.32

7. The distribution below gives the weights of 30 students of a class. Find the median weight of the students.

Solution:

Given: N = 30 and N/2= 15

Median class = 55-60

l = 55, C_f = 13, f = 6 & h = 5

Median = 55 + [(15 – 13)/6] × 5

= 55 + (10/6)

= 55 + 1.666

= 56.67

Therefore, the median weight of the students = 56.67

Exercise 14.4 Page: 293

1. The following distribution gives the daily income of 50 workers in a factory.

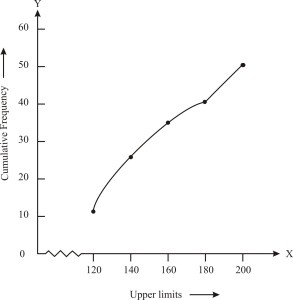
Convert the distribution above to a less than type cumulative frequency distribution and draw its ogive. - Statistics for class 10th students

Solution

Convert the given distribution table to a less than type cumulative frequency distribution, and we get

From the table plot the points corresponding to the ordered pairs such as (120, 12), (140, 26), (160, 34), (180, 40) and (200, 50) on graph paper and the plotted points are joined to get a smooth curve and the obtained curve is known as less than type ogive curve

2. During the medical check-up of 35 students of a class, their weights were recorded as follows:

Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula.

Solution:

From the given data, to represent the table in the form of graph, choose the upper limits of the class intervals are in x-axis and frequencies on y-axis by choosing the convenient scale. Now plot the points corresponding to the ordered pairs given by (38, 0), (40, 3), (42, 5), (44, 9),(46, 14), (48, 28), (50, 32) and (52, 35) on a graph paper and join them to get a smooth curve. The curve obtained is known as less than type ogive.

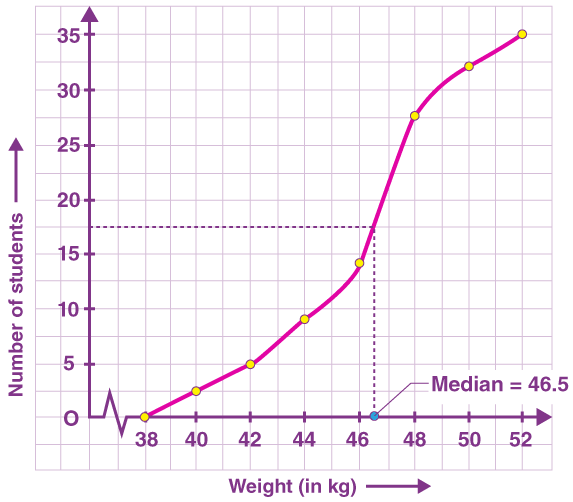
Locate the point 17.5 on the y-axis and draw a line parallel to the x-axis cutting the curve at a point. From the point, draw a perpendicular line to the x-axis. The intersection point perpendicular to x-axis is the median of the given data. Now, to find the median by making a table.

Here, N = 35 and N/2 = 35/2 = 17.5

Median class = 46 – 48

Here, l = 46, h = 2, cf= 14, f = 14

The mode formula is given as:

= 46 + [(17.5 – 14)/ 14] × 2

= 46 + 0.5

= 46 + 0.5 = 46.5

Thus, median is verified.

3. The following table gives production yield per hectare of wheat of 100 farms of a village.

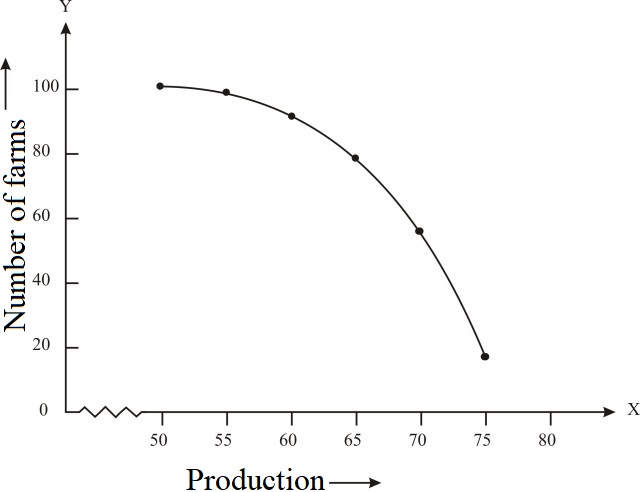
Change the distribution to a more than type distribution and draw its ogive.

Solution:

Converting the given distribution to a more than type distribution, we get

From the table obtained draw the ogive by plotting the corresponding points where the upper limits in x-axis and the frequencies obtained in the y-axis are (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) on the graph paper. The graph obtained is known as more than type ogive curve.

 

Statistics For Class 10th