JEE Advanced Previous Year Questions of Physics with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Physics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Get detailed Class 11th & 12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Click Here for JEE main Previous Year Topic Wise Questions of Physics with Solutions
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years JEE Advance Questions
Paragraph for Question 6 and 7
A fixed mass 'm' of a gas is subjected to transformation of states from K to L to M to N and back to K as shown in the figure.
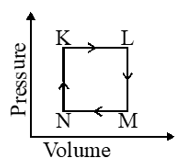
Q. Among the following, the state function(s) is (are)
(A) Internal energy
(B) Irreversible expansion work
(C) Reversible expansion work
(D) Molar enthalpy
[JEE 2009]
Ans. (A,D)
Q. One mole of an ideal gas is taken from a to b along two paths denoted by the solid and the dashed lines as shown in the graph below. If the work done along the solid line path is ws and that along the dotted line path is $\mathrm{w}_{\mathrm{d}},$ then the integer close to the ratio $\mathrm{w}_{\mathrm{d}} / \mathrm{w}_{\mathrm{s}}$ is-
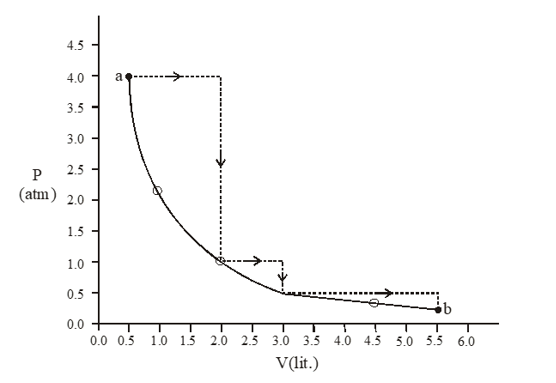 [JEE 2010]
[JEE 2010]
 [JEE 2010]
[JEE 2010]
Ans. 2
$\mathrm{W}_{\mathrm{d}}=-(4 \times 1.5)+(0)-(1 \times 1)-\left(\frac{2}{3} \times 2.5\right)$
$\mathrm{W}_{\mathrm{S}}=-\mathrm{P}_{1} \mathrm{V}_{1} \ln \frac{\mathrm{V}_{2}}{\mathrm{V}_{1}}$
$=-4 \times 05 \times \ln \frac{5.5}{0.5}$
Q. Match the transformations in Column-I with appropriate option in Column-II
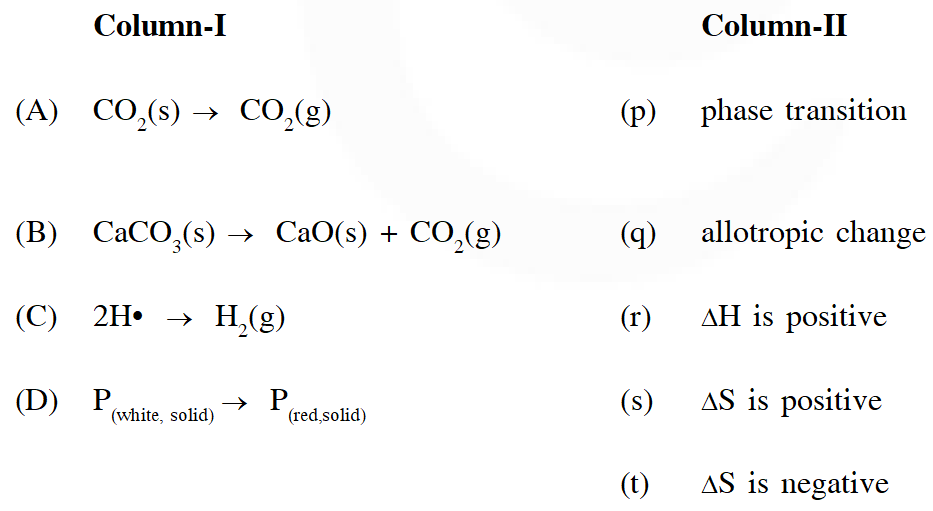 [JEE 2011]
[JEE 2011]
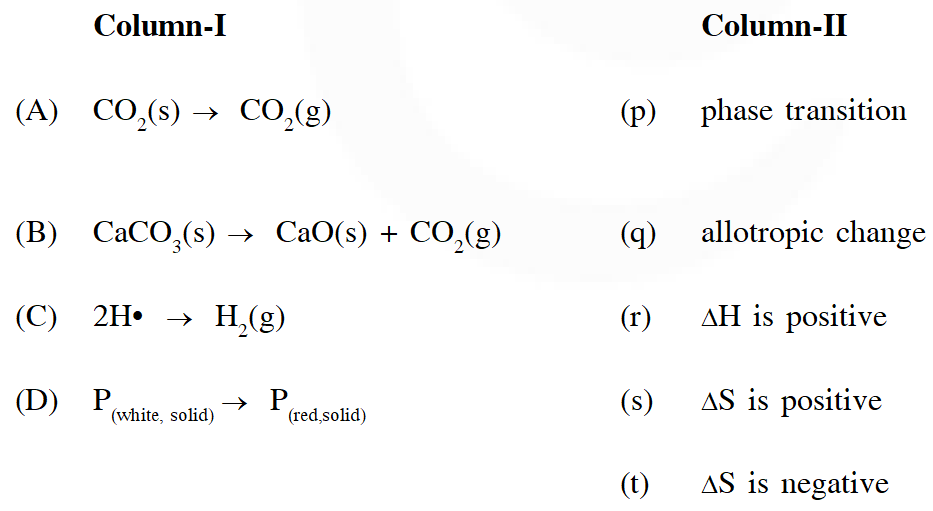 [JEE 2011]
[JEE 2011]
Ans. $A \rightarrow(P, R, S) B \rightarrow(R, S) C \rightarrow T, D \rightarrow(P, Q, T)$
Q. The reversible expansion of an ideal gas under adiabatic and isothermal conditions is shown in the figure. Which of the following statement(s) is (are) correct ?
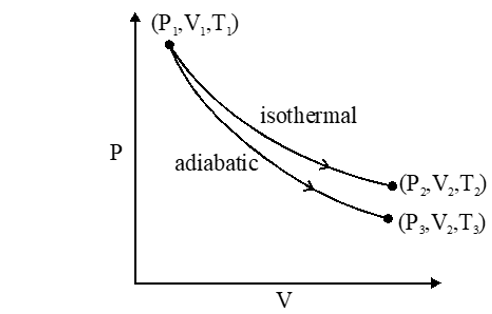 (A) $\mathrm{T}_{1}=\mathrm{T}_{2}$
(B) $\mathrm{T}_{3}>\mathrm{T}_{1}$
(C) $\mathrm{W}_{\text {isothermal }}>\mathrm{W}_{\text {adiabatic }}$
(D) $\Delta \mathrm{U}_{\text {isothemal }}>\Delta \mathrm{U}_{\text {adibaic }}$
[JEE 2012]
(A) $\mathrm{T}_{1}=\mathrm{T}_{2}$
(B) $\mathrm{T}_{3}>\mathrm{T}_{1}$
(C) $\mathrm{W}_{\text {isothermal }}>\mathrm{W}_{\text {adiabatic }}$
(D) $\Delta \mathrm{U}_{\text {isothemal }}>\Delta \mathrm{U}_{\text {adibaic }}$
[JEE 2012]
 (A) $\mathrm{T}_{1}=\mathrm{T}_{2}$
(B) $\mathrm{T}_{3}>\mathrm{T}_{1}$
(C) $\mathrm{W}_{\text {isothermal }}>\mathrm{W}_{\text {adiabatic }}$
(D) $\Delta \mathrm{U}_{\text {isothemal }}>\Delta \mathrm{U}_{\text {adibaic }}$
[JEE 2012]
(A) $\mathrm{T}_{1}=\mathrm{T}_{2}$
(B) $\mathrm{T}_{3}>\mathrm{T}_{1}$
(C) $\mathrm{W}_{\text {isothermal }}>\mathrm{W}_{\text {adiabatic }}$
(D) $\Delta \mathrm{U}_{\text {isothemal }}>\Delta \mathrm{U}_{\text {adibaic }}$
[JEE 2012]
Ans. (A,D)
Q. For an ideal gas, consider only P-V work in going from an initial state X to the final state Z. The final state Z can be reached by either of the two paths shown in the figure. Which of the following choice(s) is (are) correct ? [take S as change in entropy and w as work done]
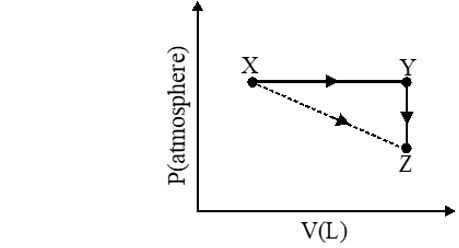 (A) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}+\Delta \mathrm{S}_{\mathrm{y} \rightarrow \mathrm{z}}$
(B) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}+\mathrm{W}_{\mathrm{y} \rightarrow \mathrm{z}}$
(C) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}$
(D) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}$
[JEE 2012]
(A) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}+\Delta \mathrm{S}_{\mathrm{y} \rightarrow \mathrm{z}}$
(B) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}+\mathrm{W}_{\mathrm{y} \rightarrow \mathrm{z}}$
(C) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}$
(D) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}$
[JEE 2012]
 (A) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}+\Delta \mathrm{S}_{\mathrm{y} \rightarrow \mathrm{z}}$
(B) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}+\mathrm{W}_{\mathrm{y} \rightarrow \mathrm{z}}$
(C) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}$
(D) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}$
[JEE 2012]
(A) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}+\Delta \mathrm{S}_{\mathrm{y} \rightarrow \mathrm{z}}$
(B) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}+\mathrm{W}_{\mathrm{y} \rightarrow \mathrm{z}}$
(C) $\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\mathrm{W}_{\mathrm{x} \rightarrow \mathrm{y}}$
(D) $\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y} \rightarrow \mathrm{z}}=\Delta \mathrm{S}_{\mathrm{x} \rightarrow \mathrm{y}}$
[JEE 2012]
Ans. (A,C)

Q. The pair of isochoric processes among the transformation of states is
(A) K to L and L to M
(B) L to M and N to K
(C) L to M and M to N
(D) M to N nd N to K
[JEE 2013]
Ans. (B)
Isochoric $\Rightarrow \mathrm{V}-$ constant
Q. The succeeding operations that enable this transformation of states are
(A) Heating, cooling, heating, cooling
(B) cooling, heating, cooling, heating
(C) Heating, cooling, cooling, heating
(D) Cooling, heating, heating, cooling
[JEE 2013]
Ans. (C) Isochoric $\Rightarrow \mathrm{V}-$ constant
Q. An ideal gas in thermally insulated vessel at internal pressure = $\mathrm{P}_{1}$, volume = $V_{1}$ and absolute temperature = $\mathrm{T}_{1}$ expands irrversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are $P_{2}$, $\mathrm{V}_{2}$ and $\mathrm{T}_{2}$, respectively. For this expansion,
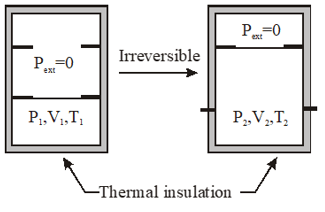 (A) q = 0
(B) $\mathrm{T}_{2}=\mathrm{T}_{1}$
(C) $\mathrm{P}_{2} \mathrm{V}_{2}=\mathrm{P}_{1} \mathrm{V}_{1}$
$(\mathrm{D}) \mathrm{P}_{2} \mathrm{V}_{2}^{\gamma}=\mathrm{P}_{1} \mathrm{V}_{1}^{\gamma}$
[JEE 2014]
(A) q = 0
(B) $\mathrm{T}_{2}=\mathrm{T}_{1}$
(C) $\mathrm{P}_{2} \mathrm{V}_{2}=\mathrm{P}_{1} \mathrm{V}_{1}$
$(\mathrm{D}) \mathrm{P}_{2} \mathrm{V}_{2}^{\gamma}=\mathrm{P}_{1} \mathrm{V}_{1}^{\gamma}$
[JEE 2014]
 (A) q = 0
(B) $\mathrm{T}_{2}=\mathrm{T}_{1}$
(C) $\mathrm{P}_{2} \mathrm{V}_{2}=\mathrm{P}_{1} \mathrm{V}_{1}$
$(\mathrm{D}) \mathrm{P}_{2} \mathrm{V}_{2}^{\gamma}=\mathrm{P}_{1} \mathrm{V}_{1}^{\gamma}$
[JEE 2014]
(A) q = 0
(B) $\mathrm{T}_{2}=\mathrm{T}_{1}$
(C) $\mathrm{P}_{2} \mathrm{V}_{2}=\mathrm{P}_{1} \mathrm{V}_{1}$
$(\mathrm{D}) \mathrm{P}_{2} \mathrm{V}_{2}^{\gamma}=\mathrm{P}_{1} \mathrm{V}_{1}^{\gamma}$
[JEE 2014]
Ans. 1,2,3
$\mathrm{q}=0 ; \mathrm{w}=0 ; \Delta \mathrm{U}=0 ; \mathrm{T}_{1}=\mathrm{T}_{2} ; \mathrm{PV}=\mathrm{constant}$
Q. One mole of an ideal gas at 300 K in thermal contact with surroundings expands isothermally from 1.0 L to 2.0 L against a constant pressure of 3.0 atm. In this process, the change in entropy of surroundings $\left(\Delta \mathrm{S}_{\text {surr }}\right)$ in $\mathrm{J} \mathrm{K}^{-1}$ is –
(1 L atm = 101.3 J)
(A) 5.763 (B) 1.013 (C) –1.013 (D) –5.763
[JEE - Advanced - 2016]
Ans. (C)


Q. For a reaction taking place in a container in equilibrium with its surroundings, the effect of temperature on its equilibrium constant K in terms of change in entropy is described by
(A) With increase in temperature, the value of K for exothermic reaction decreases because the entropy change of the system is positive
(B) With increase in temperature, the value of K for endothermic reaction increases because unfavourable change in entropy of the surroundings decreases
(C) With increase in temperature, the value of K for exothermic reaction decreases because favourable change in entropy of the surroundings decreases
(D) With increase in temperature, the value of K for endothermic reaction increases because the entropy change of the system negative
[JEE - Adv. 2017]
Ans. (B,C)
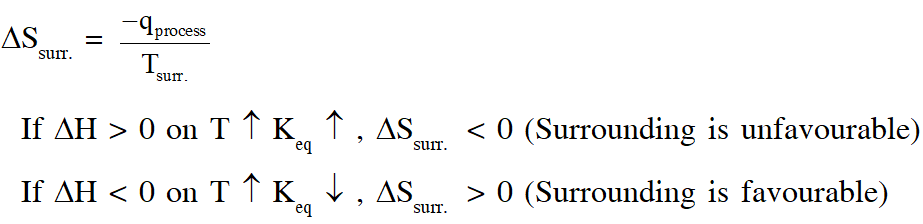
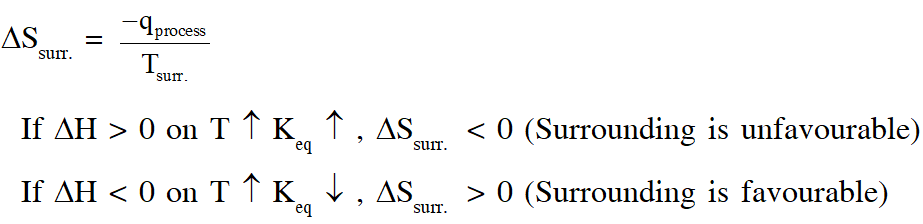
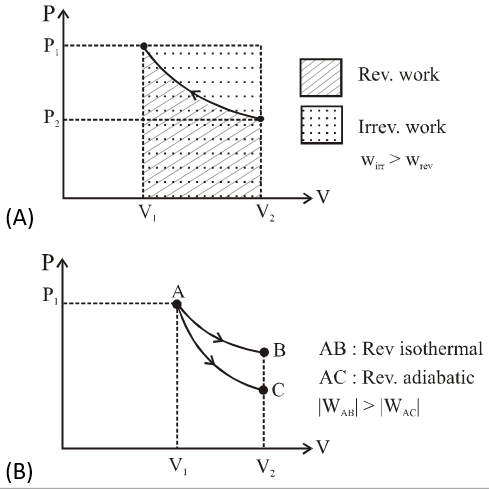
Q. An ideal gas is expanded from $\left(p_{1}, V_{1}, T_{1}\right)$ to $\left(p_{2}, V_{2}, T_{2}\right)$ under different conditions. The correct statement(s) among the following is(are)
(A) The work done on the gas is maximum when it is compressed irreversibly from ($\mathrm{p}_{2}$ , $\mathrm{V}_{2}$) to ($\mathrm{p}_{1}, \mathrm{V}_{1}$) against constant pressure $\mathrm{p}_{1}$
(B) The work done on the gas is less when it is expanded reversibly from $\mathrm{V}_{1}$ to $\mathrm{V}_{2}$ under adiabatic conditions as compared to that when expanded reversibly from $\mathrm{V}_{1}$ to $\mathrm{V}_{2}$ under isothermal conditions.
(C) The change in internal energy of the gas (i) zero, if it is expanded reversibly with $\mathrm{T}_{1} \mathrm{T}_{2}$, and (ii) positive, if it is expanded reversibly under adiabatic conditions with $\mathrm{T}_{1} \neq \mathrm{T}_{2}$
(D) If the expansion is carried out freely, it is simultaneously both isothermal as well as adiabatic
[JEE - Adv. 2017]
Ans. 1,2,4
 (3) (i) $\left.\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T}=0 \text { (isothermal hence } \Delta \mathrm{T}=0\right)$
(ii) $\Delta \mathrm{U}=\mathrm{q}+\mathrm{w}=-\mathrm{ve}(\mathrm{q}=0, \mathrm{w}<0)$
$\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T} \Rightarrow \Delta \mathrm{T}<0$
$\begin{aligned}(\mathbf{4}) \mathrm{q} &=0(\text { adiabatic }), \mathrm{w}=0(\text { free expansion }) \\ \Delta \mathrm{U} &=0 \Rightarrow \Delta \mathrm{T}=0 \text { (isothermal) } \end{aligned}$
(3) (i) $\left.\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T}=0 \text { (isothermal hence } \Delta \mathrm{T}=0\right)$
(ii) $\Delta \mathrm{U}=\mathrm{q}+\mathrm{w}=-\mathrm{ve}(\mathrm{q}=0, \mathrm{w}<0)$
$\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T} \Rightarrow \Delta \mathrm{T}<0$
$\begin{aligned}(\mathbf{4}) \mathrm{q} &=0(\text { adiabatic }), \mathrm{w}=0(\text { free expansion }) \\ \Delta \mathrm{U} &=0 \Rightarrow \Delta \mathrm{T}=0 \text { (isothermal) } \end{aligned}$
 (3) (i) $\left.\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T}=0 \text { (isothermal hence } \Delta \mathrm{T}=0\right)$
(ii) $\Delta \mathrm{U}=\mathrm{q}+\mathrm{w}=-\mathrm{ve}(\mathrm{q}=0, \mathrm{w}<0)$
$\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T} \Rightarrow \Delta \mathrm{T}<0$
$\begin{aligned}(\mathbf{4}) \mathrm{q} &=0(\text { adiabatic }), \mathrm{w}=0(\text { free expansion }) \\ \Delta \mathrm{U} &=0 \Rightarrow \Delta \mathrm{T}=0 \text { (isothermal) } \end{aligned}$
(3) (i) $\left.\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T}=0 \text { (isothermal hence } \Delta \mathrm{T}=0\right)$
(ii) $\Delta \mathrm{U}=\mathrm{q}+\mathrm{w}=-\mathrm{ve}(\mathrm{q}=0, \mathrm{w}<0)$
$\Delta \mathrm{U}=\mathrm{nC}_{\mathrm{v}} \Delta \mathrm{T} \Rightarrow \Delta \mathrm{T}<0$
$\begin{aligned}(\mathbf{4}) \mathrm{q} &=0(\text { adiabatic }), \mathrm{w}=0(\text { free expansion }) \\ \Delta \mathrm{U} &=0 \Rightarrow \Delta \mathrm{T}=0 \text { (isothermal) } \end{aligned}$
Q. A reversible cyclic process for an ideal gas is shown below. Here, P , V and T are pressure , volume and temperature , respectively. The thermodynamic parameters q, w, H and U are heat, work, enthalpy and internal energy, respectively.
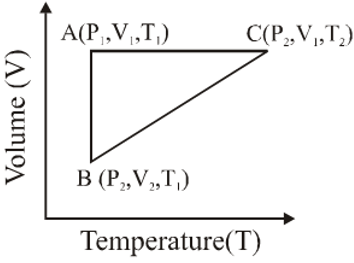 The correct option(s) is (are)
(A) $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$ and $\mathrm{w}_{\mathrm{AB}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$
(B) $\mathrm{w}_{\mathrm{BC}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$ and $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$
(C) $\Delta \mathrm{H}_{\mathrm{CA}}<\Delta \mathrm{U}_{\mathrm{CA}}$ and $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$
(D) $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$ and $\Delta \mathrm{H}_{\mathrm{CA}}>\Delta \mathrm{U}_{\mathrm{CA}}$
[JEE - Adv. 2018
The correct option(s) is (are)
(A) $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$ and $\mathrm{w}_{\mathrm{AB}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$
(B) $\mathrm{w}_{\mathrm{BC}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$ and $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$
(C) $\Delta \mathrm{H}_{\mathrm{CA}}<\Delta \mathrm{U}_{\mathrm{CA}}$ and $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$
(D) $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$ and $\Delta \mathrm{H}_{\mathrm{CA}}>\Delta \mathrm{U}_{\mathrm{CA}}$
[JEE - Adv. 2018
 The correct option(s) is (are)
(A) $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$ and $\mathrm{w}_{\mathrm{AB}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$
(B) $\mathrm{w}_{\mathrm{BC}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$ and $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$
(C) $\Delta \mathrm{H}_{\mathrm{CA}}<\Delta \mathrm{U}_{\mathrm{CA}}$ and $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$
(D) $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$ and $\Delta \mathrm{H}_{\mathrm{CA}}>\Delta \mathrm{U}_{\mathrm{CA}}$
[JEE - Adv. 2018
The correct option(s) is (are)
(A) $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$ and $\mathrm{w}_{\mathrm{AB}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$
(B) $\mathrm{w}_{\mathrm{BC}}=\mathrm{P}_{2}\left(\mathrm{V}_{2}-\mathrm{V}_{1}\right)$ and $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$
(C) $\Delta \mathrm{H}_{\mathrm{CA}}<\Delta \mathrm{U}_{\mathrm{CA}}$ and $\mathrm{q}_{\mathrm{AC}}=\Delta \mathrm{U}_{\mathrm{BC}}$
(D) $\mathrm{q}_{\mathrm{BC}}=\Delta \mathrm{H}_{\mathrm{AC}}$ and $\Delta \mathrm{H}_{\mathrm{CA}}>\Delta \mathrm{U}_{\mathrm{CA}}$
[JEE - Adv. 2018
Ans. (B,C)
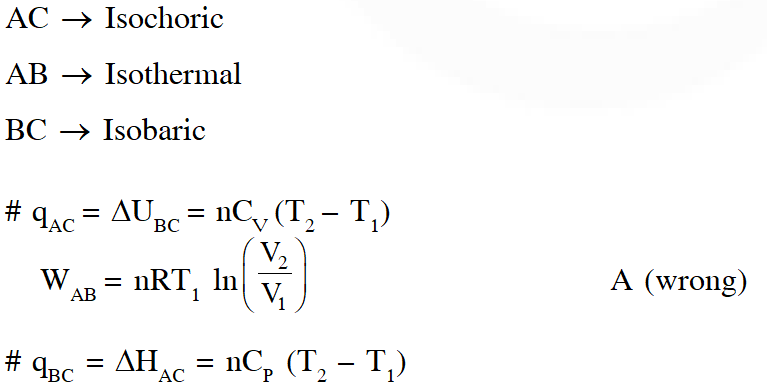
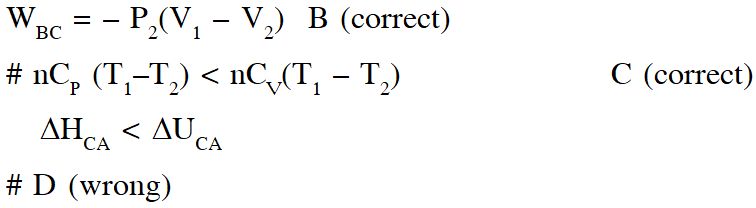
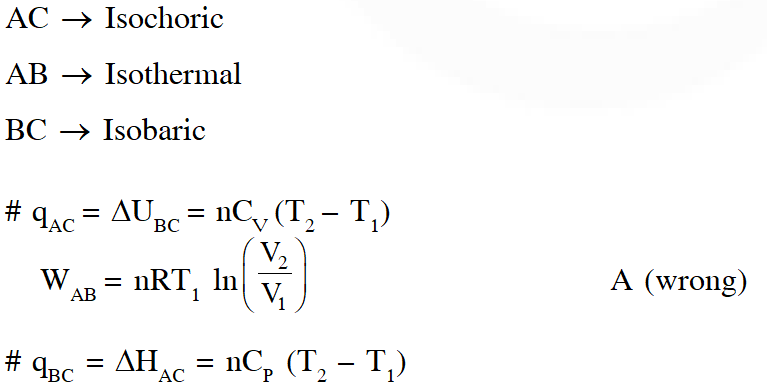
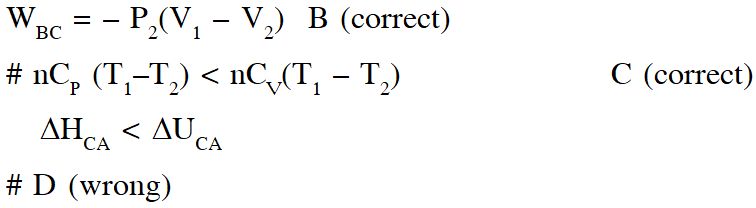
Q. For a reaction, $\mathbf{A} \square \mathbf{P}$, the plots of [A] and [P] with time at temperatures $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$ are given below.
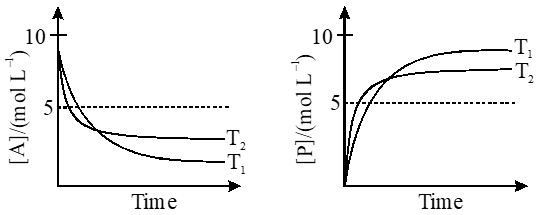 If $\mathrm{T}_{2}>\mathrm{T}_{1},$ the correct statement(s) is (are)
(Assume $\Delta \mathrm{H}^{\theta}$ and $\Delta \mathrm{S}^{\theta}$ are independent of temperature and ratio of $\ln \mathrm{K}$ at $\mathrm{T}_{1}$ to $\ln \mathrm{K}$ at $\mathrm{T}_{2}$ is greater than $\mathrm{T}_{2 / \mathrm{T}_{\mathrm{T}}}$. Here H, S, G and K are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)
(A) $\Delta \mathrm{H}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(B) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{H}^{\theta}>0$
(C) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(D) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}>0$
[JEE - Adv. 2018]
If $\mathrm{T}_{2}>\mathrm{T}_{1},$ the correct statement(s) is (are)
(Assume $\Delta \mathrm{H}^{\theta}$ and $\Delta \mathrm{S}^{\theta}$ are independent of temperature and ratio of $\ln \mathrm{K}$ at $\mathrm{T}_{1}$ to $\ln \mathrm{K}$ at $\mathrm{T}_{2}$ is greater than $\mathrm{T}_{2 / \mathrm{T}_{\mathrm{T}}}$. Here H, S, G and K are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)
(A) $\Delta \mathrm{H}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(B) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{H}^{\theta}>0$
(C) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(D) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}>0$
[JEE - Adv. 2018]
 If $\mathrm{T}_{2}>\mathrm{T}_{1},$ the correct statement(s) is (are)
(Assume $\Delta \mathrm{H}^{\theta}$ and $\Delta \mathrm{S}^{\theta}$ are independent of temperature and ratio of $\ln \mathrm{K}$ at $\mathrm{T}_{1}$ to $\ln \mathrm{K}$ at $\mathrm{T}_{2}$ is greater than $\mathrm{T}_{2 / \mathrm{T}_{\mathrm{T}}}$. Here H, S, G and K are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)
(A) $\Delta \mathrm{H}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(B) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{H}^{\theta}>0$
(C) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(D) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}>0$
[JEE - Adv. 2018]
If $\mathrm{T}_{2}>\mathrm{T}_{1},$ the correct statement(s) is (are)
(Assume $\Delta \mathrm{H}^{\theta}$ and $\Delta \mathrm{S}^{\theta}$ are independent of temperature and ratio of $\ln \mathrm{K}$ at $\mathrm{T}_{1}$ to $\ln \mathrm{K}$ at $\mathrm{T}_{2}$ is greater than $\mathrm{T}_{2 / \mathrm{T}_{\mathrm{T}}}$. Here H, S, G and K are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)
(A) $\Delta \mathrm{H}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(B) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{H}^{\theta}>0$
(C) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}<0$
(D) $\Delta \mathrm{G}^{\theta}<0, \Delta \mathrm{S}^{\theta}>0$
[JEE - Adv. 2018]
Ans. (A,C)
Comments
Faizal
Sept. 25, 2020, 2:40 a.m.
Sir Kisan bill kahe pass kr diye
Bahut galat kiya
....
....
.... Tu to giyo Modi
chitty
Sept. 17, 2020, 4:59 p.m.
not having sufficient previous questions ,please update those which are helpful in tests
