JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Simulator
Previous Years AIEEE/JEE Main Questions
Q. Assuming the gas to be ideal the work done on the gas in taking it from A to B is :-
(1) 400 R (2) 500 R (3) 200 R (4) 300
[AIEEE-2009]
Ans. (1)
Q. The work done on the gas in taking it from D to A is :-
(1) –690 R (2) +690 R (3) –414 R (4) +414 R
[AIEEE-2009]
Ans. (4)
Q. The net work done on the gas in the cycle ABCDA is :-
(1) 1076 R (2) 1904 R (3) Zero (4) 276 R
[AIEEE-2009]
Ans. (4)
Q. A diatomic ideal gas is used in a carnot engine as the working substance. If during the adiabatic expansion part of the cycle the volume of the gas increases from V to 32 V, the efficiency of the engine is :-
(1) 0.25 (2) 0.5 (3) 0.75 (4) 0.99
[AIEEE-2010]
Ans. (3)
Q. A Carnot engine operating between temperatures $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$ has efficientcy $\frac{1}{6} .$ When $\mathrm{T}_{2}$ is lowered
by $62 \mathrm{K},$ its efficiency increases to $\frac{1}{3} .$ Then $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$ are, respectively:-
(1) 330 K and 268 K (2) 310 K and 248 K (3) 372 K and 310 K (4) 372 K and 330 K
[AIEEE-2011]
Ans. (3)
Q. The specific heat capacity of a metal at low temperautre (T) is given as $\mathrm{C}_{\mathrm{p}}\left(\mathrm{kJk}^{-1} \mathrm{kg}^{-1}\right)=32\left(\frac{\mathrm{T}}{400}\right)^{3}$ A 100 gram vessel of this metal is to be cooled from 20°K to 4°K by a special refrigerator operating at room temperature (27°C). The amount of work required to cool the vessel is:-
(1) equal to 0.002 kJ
(2) greater than 0.148 kJ
(3) between 0.148 kJ and 0.028 kJ
(4) less than 0.028 kJ
[AIEEE-2011]
Ans. (3)
Q. A container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated. If the valve is suddenly opened, the pressure and temperature of the gas will be :-
(1) $\frac{\mathrm{P}}{2}, \mathrm{T}$
(2) $\frac{\mathrm{P}}{2}, \frac{\mathrm{T}}{2}$
(3) P, T
(4) $\mathrm{P}, \frac{\mathrm{T}}{2}$
[AIEEE-2011]
Ans. (1)
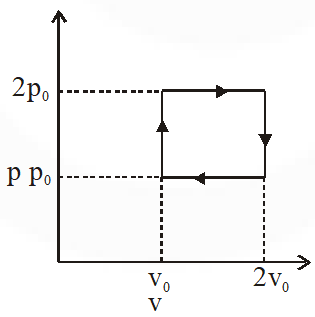
Q. Helium gas goes through a cycle ABCDA (consisting of two isochoric and two isobaric lines) as shown in figure. Efficiency of this cycle is nearly (Assume the gas to be close to ideal gas) :-
 [AIEEE-2012]
[AIEEE-2012]
 [AIEEE-2012]
[AIEEE-2012]
Ans. (2)
Q. A Carnot engine, whose efficiency is 40% takes in heat from a source maintained at a temperature of 500 K. It is desired to have an engine of efficiency 60%. Then, the intake temperature for the same exhaust (sink) temperature must be :-
(1) 600 K
(2) efficiency of Carnot engine cannot be made larger than 50%
(3) 1200 K
(4) 750 K
[AIEEE-2012]
Ans. (4)
Q. The above p-v diagram represents the thermodynamic cycle of an engine, operating with an ideal monoatomic gas. The amount of heat, extracted from the source in a single cycle is :
 (1) $\mathrm{p}_{0} \mathrm{v}_{0}$
( 2)$\left(\frac{13}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
( 3)$\left(\frac{11}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
(4) $4 \mathrm{p}_{0} \mathrm{v}_{0}$
[jEE-Mains-2013]
(1) $\mathrm{p}_{0} \mathrm{v}_{0}$
( 2)$\left(\frac{13}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
( 3)$\left(\frac{11}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
(4) $4 \mathrm{p}_{0} \mathrm{v}_{0}$
[jEE-Mains-2013]
 (1) $\mathrm{p}_{0} \mathrm{v}_{0}$
( 2)$\left(\frac{13}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
( 3)$\left(\frac{11}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
(4) $4 \mathrm{p}_{0} \mathrm{v}_{0}$
[jEE-Mains-2013]
(1) $\mathrm{p}_{0} \mathrm{v}_{0}$
( 2)$\left(\frac{13}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
( 3)$\left(\frac{11}{2}\right) \mathrm{p}_{0} \mathrm{v}_{0}$
(4) $4 \mathrm{p}_{0} \mathrm{v}_{0}$
[jEE-Mains-2013]
Ans. (2)
Q. One mole of diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperatures at A, B and C are 400 K, 800 K and 600 K respectively. Choose the correct statement :
 [jEE-Mains-2014]
[jEE-Mains-2014]
 [jEE-Mains-2014]
[jEE-Mains-2014]
Ans. (2)
Q. Consider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume $\mathrm{u}=\frac{\mathrm{U}}{\mathrm{V}} \propto \mathrm{T}^{4}$ and pressure $\mathrm{p}=\frac{1}{3}\left(\frac{\mathrm{U}}{\mathrm{v}}\right)$. If the shell now undergoes an adiabatic expansion the relation between T and R is –
(1) $\mathrm{T} \propto \frac{1}{\mathrm{R}}$
(2) $\mathrm{T} \propto \frac{1}{\mathrm{R}^{3}}$
(3) T $\propto \mathrm{e}^{-\mathrm{R}}$
(4) $\mathrm{T} \propto \mathrm{e}^{-3 \mathrm{R}}$
[jEE-Mains-2015]
Ans. (1)
Q. 'n' moles of an ideal gas undergoes a process $\mathrm{A} \rightarrow \mathrm{B}$ as shown in the figure. The maximum temperature of the gas during the process will be :
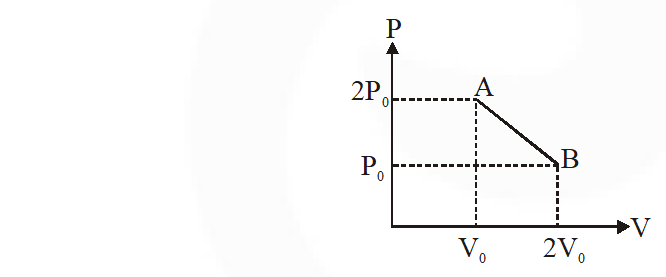 (1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (3) $\frac{3 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$ (4) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$
[jEE-Mains-2016]
(1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (3) $\frac{3 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$ (4) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$
[jEE-Mains-2016]
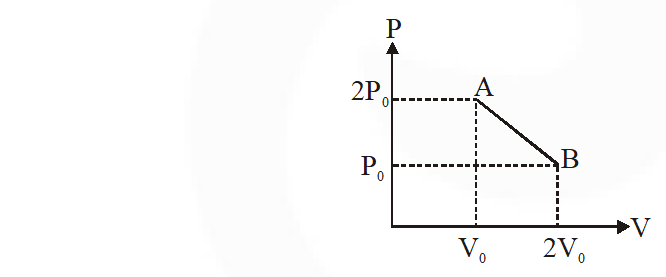 (1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (3) $\frac{3 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$ (4) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$
[jEE-Mains-2016]
(1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (1) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{\mathrm{nR}}$ (3) $\frac{3 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$ (4) $\frac{9 \mathrm{P}_{0} \mathrm{V}_{0}}{2 \mathrm{nR}}$
[jEE-Mains-2016]
Ans. (2)
Q. An ideal gas undergoes a quasi static, reversible process in which its molar heat capacity C remains constant. If during this process the relation of pressure P and volume V is given by $\mathrm{P} \mathrm{V}^{\mathrm{n}}$ = constant, then n is given by (Here $\mathrm{C}_{\mathrm{P}}$ and $\mathrm{C}_{\mathrm{v}}$ are molar specific heat at constant pressure and constant volume, respectively) :-
(1) $\mathrm{n}=\frac{\mathrm{C}-\mathrm{C}_{\mathrm{V}}}{\mathrm{C}-\mathrm{C}_{\mathrm{P}}}$
(2) $\mathrm{n}=\frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}$
(3) $\quad \mathrm{n}=\frac{\mathrm{C}-\mathrm{C}_{\mathrm{P}}}{\mathrm{C}-\mathrm{C}_{\mathrm{V}}}$
(4) $\mathrm{n}=\frac{\mathrm{C}_{\mathrm{P}}-\mathrm{C}}{\mathrm{C}-\mathrm{C}_{\mathrm{V}}}$
[jEE-Mains-2016]
Ans. (3)
Q. $\mathrm{C}_{\mathrm{p}}$ and $\mathrm{C}_{\mathrm{v}}$ are specific heats at constant pressure and constant volume respectively. It is observed that
$\mathrm{C}_{\mathrm{p}}-\mathrm{C}_{\mathrm{v}}=$ = a for hydrogen gas $\mathrm{C}_{\mathrm{p}}-\mathrm{C}_{\mathrm{v}}=$ = b for nitrogen gas The correct relation between a and b is :
(1) a = 14 b
(2) a = 28 b
(3) $a=\frac{1}{14} b$
(4) a = b
[jEE-Mains-2017]
Ans. (1)
Q. Two moles of an ideal monoatomic gas occupies a volume V at $27^{\circ}$ C. The gas expands adiabatically to a volume 2V. Calculate (a) the final temperature of the gas and (b) change in its internal energy.
(1) (a) 195 K (b) –2.7 kJ
(2) (a) 189 K (b) –2.7 kJ
(3) (a) 195 K (b) 2.7 kJ
(4) (a) 189 K (b) 2.7 kJ
[jEE-Mains-2018]
Ans. (2)
Comments
Abhishek
March 2, 2023, 5:48 p.m.
Sir 2018 tk ke hi kiu hai q 2019 ,20,21,22, ke bhi provide kra dijiye plzz 🙏🙏
sonu
Feb. 27, 2021, 10:55 a.m.
AIEEE 2012 and Mains 2013 asked the same question but mains 2013 only asked for Q2 (extracted heat). So will it not be 3rd option (11/2) ?
Suggestion
Aug. 9, 2020, 10:09 a.m.
Post the questions completely with graphs & give the solutions for the questions.
