Now we have the basic idea of what is Electric Charge. So, the next step is How two charges interact with each other? How do they interact with each other? What all parameters affect the forces they exert on each other? What is the resultant force and in what is its direction? Here we are going to know more about Vector form of Coulomb’s Law to get answers of all these questions.
So, let’s begin!!
If q1 & q2 are charges, r is the distance between them and F is the force acting between them
Then, F ∝ q1q2
F ∝ 1/r²
∴ F ∝ ${{{q_1}{q_2}} \over {{r^2}}}$
Or $F = C{{{q_1}{q_2}} \over {{r^2}}}$
[caption id="attachment_4246" align="aligncenter" width="298"]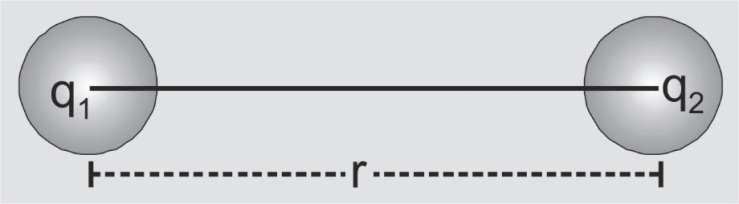
Coulomb's law depiction of 2 Electric charges[/caption]
C is const. which depends upon system of units and also on medium between two charges.
In SI unit,
C = 1 in electrostatic unit (esu)
ε0 = 8.85 × 10–12 C²/Nm² = permittivity of free space or vacuum
Fair =${1 \over {4\pi {\varepsilon _0}}}{{{q_1}{q_2}} \over {{r^2}}}$ and Fmedium = ${1 \over {4\pi {\varepsilon _0}{\varepsilon _r}}}{{{q_1}{q_2}} \over {{r^2}}}$
${{{F_{medium}}} \over {{F_{air}}}} = {1 \over {{\varepsilon _r}}}$= K
εr or K = Dielectric constant or Relative permittivity or specific inductive capacity of medium.
The dielectric constants of different mediums are:
$\mathop {{F_{21}}}\limits^ \to = {1 \over {4\pi {\varepsilon _0}{\varepsilon _r}}}\,\,\,{{{q_1}{q_2}} \over {r_{12}^2}}\,\,{\hat r_{12}}$
[caption id="attachment_4247" align="aligncenter" width="303"]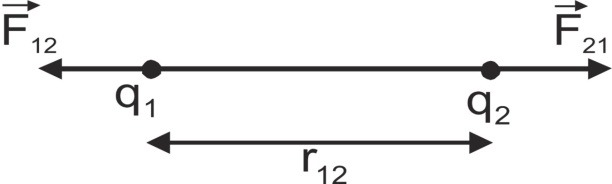
Vector form of Coulomb's Law[/caption]
$\mathop {{F_{12}}}\limits^ \to $= Force on q1 due to q2
$\mathop {{F_{12}}}\limits^ \to = {1 \over {4\pi {\varepsilon _0}{\varepsilon _r}}}\,\,\,{{{q_1}{q_2}} \over {r_{21}^2}}\,\,{\hat r_{21}}$
$\mathop {{F_{12}}}\limits^ \to = - \mathop {{F_{21}}}\limits^ \to $ (∵ ${\hat r_{12}} = - {\hat r_{21}}$ )
Or ${\mathop F\limits^ \to _{12}} + {\mathop F\limits^ \to _{21}} = 0$
This is known as Vector form of Coulomb's Law.
(b) Both the forces obey inverse square law i.e., F ∝ (1/r²).
(c) Both are conservative forces, i.e., the work done by these is independent of the nature of path.
(d) Both the forces can operate in vacuum.
(b) The gravitational force is independent of medium while electrostatic force depends on nature of medium.
(c) Electrostatic forces are very large as compared to gravitational forces.
For an electron-proton system, electrostatic force of attraction
${F_e} = {1 \over {4\pi {\varepsilon _0}}}{{e.e} \over {{r^2}}} = 9 \times {10^9}.{{{{(1.6 \times {{10}^{ - 19}})}^2}} \over {{r^2}}}$N
where ‘r’ meter is the separation between the electron and proton,
Force of gravitational attraction ${F_g} = G{{{m_e}{m_p}} \over {{r^2}}} = 6.67 \times {10^{ - 11}}.{{(9.1 \times {{10}^{ - 31}}) \times (1.67 \times {{10}^{ - 27}})} \over {{r^2}}}N$
Thus,${{{F_e}} \over {{F_g}}} = 2.26 \times {10^{39}}$ i.e., electrostatic force between a proton and an electron is about 1039 times stronger than the gravitational force.
- Coulomb’s Law definition
- Effect of Medium
- Vector form of Coulomb's Law
- Important Points on Coulomb’s Law
- Comparison of Electrostatic and Gravitational Forces
- Coulomb’s Law Examples
Coulomb's Law Definition
The force of attraction or repulsion between two stationary point charges is directly proportional to the product of charges and inversely proportional to the square of distance between them. This force acts along the line joining the center of two charges.If q1 & q2 are charges, r is the distance between them and F is the force acting between them
Then, F ∝ q1q2
F ∝ 1/r²
∴ F ∝ ${{{q_1}{q_2}} \over {{r^2}}}$
Or $F = C{{{q_1}{q_2}} \over {{r^2}}}$
[caption id="attachment_4246" align="aligncenter" width="298"]
Coulomb's law depiction of 2 Electric charges[/caption]
C is const. which depends upon system of units and also on medium between two charges.
In SI unit,
C = 1 in electrostatic unit (esu)
ε0 = 8.85 × 10–12 C²/Nm² = permittivity of free space or vacuum
Effect of medium
The dielectric constant of a medium is the ratio of the electrostatic force between two charges separated by a given distance in air to electrostatic force between same two charges separated by same distance in that medium.Fair =${1 \over {4\pi {\varepsilon _0}}}{{{q_1}{q_2}} \over {{r^2}}}$ and Fmedium = ${1 \over {4\pi {\varepsilon _0}{\varepsilon _r}}}{{{q_1}{q_2}} \over {{r^2}}}$
${{{F_{medium}}} \over {{F_{air}}}} = {1 \over {{\varepsilon _r}}}$= K
εr or K = Dielectric constant or Relative permittivity or specific inductive capacity of medium.
- Permittivity: Permittivity is a measure of the ability of the medium surrounding electric charges to allow electric lines of force to pass through it. It determines the forces between the charges.
- Relative Permittivity: The relative permittivity or the dielectric constant (εr or K) of a medium is defined as the ratio of the permittivity ε of the medium to the permittivity ε0 of free space i.e. εr or $K = {\varepsilon \over {{\varepsilon _0}}}$
The dielectric constants of different mediums are:
| Medium | Vacuum | Air | Water | Mica | Teflon | Glass | PVC | Metal |
| εr | 1 | 1.00059 | 80 | 6 | 2 | 5-10 | 4.5 | ∞ |
Vector form of Coulomb's Law
The electrical force, like all forces, is typically expressed using the unit Newton. Being a force, the strength of the electrical interaction is a vector quantity that has both magnitude and direction. The direction of the electrical force is dependent upon whether the charged objects are charged with like charge or opposite charge. [source]
The direction of the force acting between two charges also depends on their nature and it is along the line joining the center of two charges.
$\mathop {{F_{21}}}\limits^ \to $= force on q2 due to q1$\mathop {{F_{21}}}\limits^ \to = {1 \over {4\pi {\varepsilon _0}{\varepsilon _r}}}\,\,\,{{{q_1}{q_2}} \over {r_{12}^2}}\,\,{\hat r_{12}}$
[caption id="attachment_4247" align="aligncenter" width="303"]
Vector form of Coulomb's Law[/caption]
$\mathop {{F_{12}}}\limits^ \to $= Force on q1 due to q2
$\mathop {{F_{12}}}\limits^ \to = {1 \over {4\pi {\varepsilon _0}{\varepsilon _r}}}\,\,\,{{{q_1}{q_2}} \over {r_{21}^2}}\,\,{\hat r_{21}}$
$\mathop {{F_{12}}}\limits^ \to = - \mathop {{F_{21}}}\limits^ \to $ (∵ ${\hat r_{12}} = - {\hat r_{21}}$ )
Or ${\mathop F\limits^ \to _{12}} + {\mathop F\limits^ \to _{21}} = 0$
This is known as Vector form of Coulomb's Law.
Important Points on Coulomb’s Law
- The electrostatic force is a medium dependent force.
- The electrostatic force is an action-reaction pair, i.e., the force exerted by one charge on the other is equal and opposite to the force exerted by the other on the first.
- The force is conservative, i.e., work done in moving a point charge around a closed path under the action of Coulomb's force is zero.
- Coulomb's law is applicable to point charges only. But it can be applied for distributed charges also.
- This law is valid only for stationary point charges and cannot be applied for moving charges.
- The law expresses the force between two-point charges at rest. In applying it to the case of extended bodies of finite size care should be taken in assuming the whole charge of a body to be concentrated at its 'center' as this is true only for spherically charged body, that too for a external point.
- The equilibrium of a charged particle under the action of Coulombian forces alone can never be stable. This statement is called Earnshaw's theorem.
- Unit of charge: $F = {1 \over {4\pi {\varepsilon _0}}}\,\,{{{q_1}{q_2}} \over {{r^2}}}$ If q1 = q2 = 1 coulomb, r = 1m then $F = {1 \over {4\pi {\varepsilon _0}}}\,\,$ = 9 × 109 N One Coulomb of charge is that charge which when placed at rest in vacuum at a distance of one meter from an equal and similar stationary charge is repelled by it with a force of 9 × 109 Newton.
Comparison of Electrostatic and Gravitational Forces
Two charged bodies experience electrostatic force and also a gravitational force on account of their masses.Similarities:
(a) Both the forces are central forces, i.e., they act along the line joining the center of two charges or masses.(b) Both the forces obey inverse square law i.e., F ∝ (1/r²).
(c) Both are conservative forces, i.e., the work done by these is independent of the nature of path.
(d) Both the forces can operate in vacuum.
Differences:
(a) The gravitational forces are always attractive while the electrostatic forces may be attractive or repulsive.(b) The gravitational force is independent of medium while electrostatic force depends on nature of medium.
(c) Electrostatic forces are very large as compared to gravitational forces.
For an electron-proton system, electrostatic force of attraction
${F_e} = {1 \over {4\pi {\varepsilon _0}}}{{e.e} \over {{r^2}}} = 9 \times {10^9}.{{{{(1.6 \times {{10}^{ - 19}})}^2}} \over {{r^2}}}$N
where ‘r’ meter is the separation between the electron and proton,
Force of gravitational attraction ${F_g} = G{{{m_e}{m_p}} \over {{r^2}}} = 6.67 \times {10^{ - 11}}.{{(9.1 \times {{10}^{ - 31}}) \times (1.67 \times {{10}^{ - 27}})} \over {{r^2}}}N$
Thus,${{{F_e}} \over {{F_g}}} = 2.26 \times {10^{39}}$ i.e., electrostatic force between a proton and an electron is about 1039 times stronger than the gravitational force.
Vector form of Coulomb’s Law Examples
Q. Three equal charges Q each are placed on the vertices of an equilateral triangle of side a. What is the resultant force on any one charge due to the other two?
Ans. The charges are shown in fig.
The resultant force $F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos 60^\circ } $
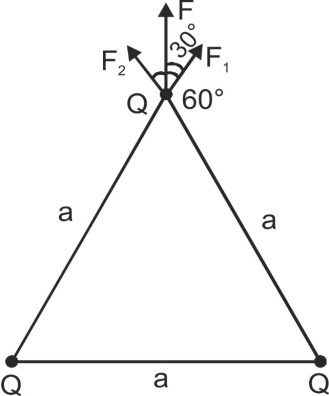
With F1 = F2 = kQ2/a2 $F = {{\sqrt 3 k{Q^2}} \over {{a^2}}}$
From symmetry the direction is along y-axis.
The resultant force $F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos 60^\circ } $
With F1 = F2 = kQ2/a2 $F = {{\sqrt 3 k{Q^2}} \over {{a^2}}}$
From symmetry the direction is along y-axis.
Q. Two equally charged identical metal spheres A and B repel each other with a force of 2 × 10–5 N. Another identical uncharged sphere C is touched to B and then placed at the mid-point between A and B. What is the net electric force on C?
Ans. Let initially the charge on each sphere is q and separation between their centers is r:
$F = {1 \over {4\pi {\varepsilon _0}}}{{q \times q} \over {{r^2}}} = 2 \times {10^{ - 5}}N$
When sphere C touches B, the charge of B, q will distribute equally on B and C as spheres are identical now: qB = qC = (q/2)
So, sphere C will experience a force
${F_{CA}} = {1 \over {4\pi {\varepsilon _0}}}{{q\left( {q/2} \right)} \over {{{\left( {r/2} \right)}^2}}} = 2F$ along $\mathop {AB}\limits^ \to $ due to charge on A
and, ${F_{CB}} = {1 \over {4\pi {\varepsilon _0}}}{{(q/2)\,(q/2)} \over {{{(r/2)}^2}}} = F$ along $\mathop {BA}\limits^ \to $ due to charge on B
So, the net force on C due to charges on A and B,
FC = FCA – FCB = 2F – F = F = 2 × 10–5 N along $\mathop {AB}\limits^ \to $.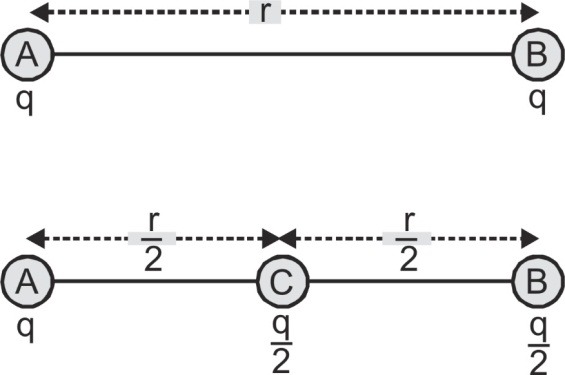
$F = {1 \over {4\pi {\varepsilon _0}}}{{q \times q} \over {{r^2}}} = 2 \times {10^{ - 5}}N$
When sphere C touches B, the charge of B, q will distribute equally on B and C as spheres are identical now: qB = qC = (q/2)
So, sphere C will experience a force
${F_{CA}} = {1 \over {4\pi {\varepsilon _0}}}{{q\left( {q/2} \right)} \over {{{\left( {r/2} \right)}^2}}} = 2F$ along $\mathop {AB}\limits^ \to $ due to charge on A
and, ${F_{CB}} = {1 \over {4\pi {\varepsilon _0}}}{{(q/2)\,(q/2)} \over {{{(r/2)}^2}}} = F$ along $\mathop {BA}\limits^ \to $ due to charge on B
So, the net force on C due to charges on A and B,
FC = FCA – FCB = 2F – F = F = 2 × 10–5 N along $\mathop {AB}\limits^ \to $.
Q. Force F is acting between two charges. If a sheet of glass (εr = 6) is placed between the two charges, what will be the force?
Ans. $F = {1 \over {4\pi {\varepsilon _0}}}{{{q_1}{q_2}} \over {{r^2}}}$
or $F' = {1 \over {4\pi { \in _0}K}}{{{q_1}{q_2}} \over {{r^2}}}$
or $F' = {F \over K} = {F \over 6}$
Q. How should we divide a charge 'Q' to get maximum force of repulsion between them?
Ans. Let q & Q – q be the two parts.
$F = {1 \over {4\pi {\varepsilon _0}}}{{q\left( {Q - q} \right)} \over {{r^2}}}$
for maximum F, ${{dF} \over {dq}} = 0$
or ${1 \over {4\pi {\varepsilon _0}}}{{Q - 2q} \over {{r^2}}} = 0$
or $q = {Q \over 2}$
Hence Q should be divided in two equal parts.