Some applications of General Equation
(A) Projection from a height at an angle $\theta$ above horizontal :
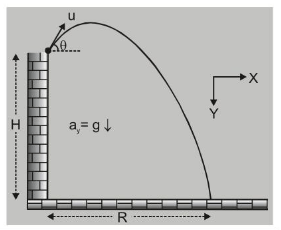$u_{x}=u \cos \theta \quad \quad u_{y}=-u \sin \theta$
$x=(u \cos \theta) t \quad a_{y}=+g$
$h=(-u \sin \theta) t+\frac{1}{2} g t^{2}$
$g t^{2}-(2 u \sin \theta) t-2 h=0$
$\mathrm{t}=\frac{+2 \mathrm{u} \sin \theta \pm \sqrt{(2 \mathrm{u} \sin \theta)^{2}+8 \mathrm{hg}}}{2 \mathrm{~g}}$
or $\quad t=\frac{u \sin \theta}{g} \pm \sqrt{\left(\frac{u \sin \theta}{g}\right)^{2}+\frac{2 h}{g}}$
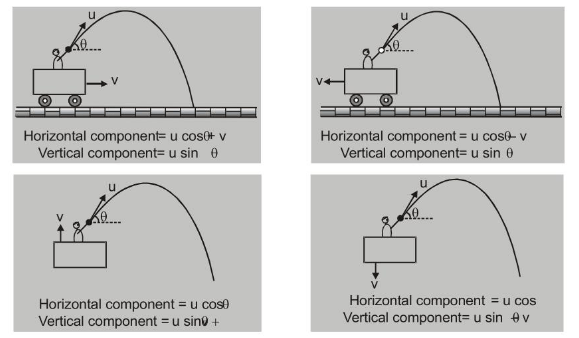
(B) Projection from a moving body :
Consider a man who throws a ball from a moving trolley. Let the velocity of ball relative to man be $u$
$\vec{V}_{\text {ball, trolley }}=\vec{V}_{\text {ball }}-\vec{V}_{\text {trolley }} \quad$ i.e. $\quad \vec{V}_{\text {ball }}=\vec{V}_{\text {ball, trolley }}+\vec{V}_{\text {trolley }}$
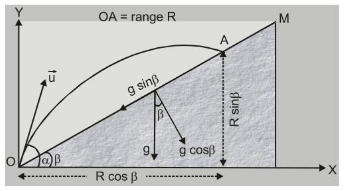(C) Projection on an inclined plane :
$a_{x}=-g \sin \beta \quad a_{y}=-g \cos \beta$
$u_{x}=u \cos (\alpha-\beta) \quad u_{y}=u \sin (\alpha-\beta)$
or $\quad T=\frac{2 u \sin (\alpha-\beta)}{g \cos \beta} \mid$ is the time of flight
$x=u_{x} t+\frac{1}{2} a_{x} t^{2} \quad$ gives the Range $R=\frac{2 u^{2} \sin (\alpha-\beta) \cos \alpha}{g \cos ^{2} \beta}$
Ex. If $t_{1}$ be the time taken by a body to clear the top of a building and $t_{2}$ be the time spent in air, find the ratio $t_{2}: t_{1}$.
Sol. Total time of flight $=2$ (time taken to reach max. height) $\Rightarrow t_{2}=2 t_{1} \quad \Rightarrow \frac{t_{2}}{t_{1}}=\frac{2}{1}$
Ex. When the angle of elevation of a gun are $60^{\circ}$ and $30^{\circ}$ respectively. The height it shoots are $h_{1}$ and $\mathrm{h}_{2}$ respectively. Find the ratio $\mathrm{h}_{1} / \mathrm{h}_{2}$.
Sol. For angle of elevation of $60^{\circ}$, we have maximum height $h_{1}=\frac{u^{2} \sin ^{2} 60^{\circ}}{2 g}=\frac{3 u^{2}}{8 g}$
For angle of elevation of $30^{\circ}$, we have maximum height $h_{2}=\frac{u^{2} \sin ^{2} 30^{\circ}}{2 g}=\frac{u^{2}}{8 g}$
$\frac{\mathrm{h}_{1}}{\mathrm{~h}_{2}}=\frac{3}{1}$
Ex. From a certain height above the ground, a stone $P$ is dropped gently. Simultaneously, another stone $\mathrm{Q}$ is thrown horizontally. Which of the two stones will arrive at the ground earlier?
Sol. Both the stones will reach the ground at the same time. This result follows from the physical independence of horizontal and vertical motions.
Ex. A gun, kept on a straight horizontal road, is used to hit a car travelling along the same road away from the gun with a uniform sped of $72 \mathrm{~km} / \mathrm{hr}$. The car is at a distance of $500 \mathrm{~m}$ from the gun, when the gun is fired at an angle of $45^{\circ}$ with the horizontal.
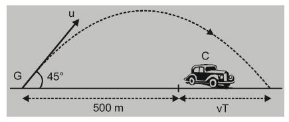Find
(a) the distance of the car from the gun when the shell hits it;
(b) The speed of projection of the shell from the gun. $\left(\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}\right)$
Sol. The speed of the car $v=72 \times(5 / 18)=20 \mathrm{~m} / \mathrm{s}$
The time of flight of projectile $T=\frac{2 u \sin \theta}{g}=\frac{u \sqrt{2}}{g} \quad$ [as $\theta=45^{\circ}$ ] ...(1)
and range of projectile $R=\frac{u^{2} \sin 2 \theta}{g}=\frac{u^{2}}{g}$ ...(2)
During the flight of shell, the car will cover a distance $R=500+v T$
Substituting the values of $T$ and $R$
form Eqn. (1) and (2) in the above,
$\frac{u^{2}}{g}=500+\frac{u \sqrt{2}}{g} \times 20$
or $\quad u^{2}-20 \sqrt{2} u-4900=0$
or $\quad u=(1 / 2)[20 \sqrt{2} \pm \sqrt{(800+4 \times 4900}]$
or $\quad u=10[\sqrt{2} \pm \sqrt{51}]$
As negative sign of $u$ is physically unacceptable,
$\mathrm{u}=10[1.414+7.141]=85.56 \mathrm{~m} / \mathrm{s}$
Substituting the above value of $u$ in Eqn. (2)
$\mathrm{R}=\frac{\mathrm{u}^{2}}{\mathrm{~g}}=\frac{(85.56)^{2}}{9.8}=746.9 \mathrm{~m}$
Ex. Two particle located at a point begin to move with velocities $4 \mathrm{~m} / \mathrm{s}$ and $1 \mathrm{~m} / \mathrm{s}$ horizontally in opposite directions. Determine the time when their velocity vectors become perpendicular. Assume that the motion takes place in a uniform gravitational field of strength $\mathrm{g}$.
Sol. Velocity of first particle at time $t=4 \hat{i}-g t \hat{j}$
Velocity of second particle at time $t=-\hat{\mathrm{i}}-\mathrm{gt} \hat{\mathrm{j}}$
Since the dot product of perpendicular vectors is zero therefore
$(4 \hat{i}-g t \hat{j}) \cdot(-\hat{i}-g t \hat{j})=0$
or $\quad=4+g^{22} t^{2}=0 \quad$ or $\quad g^{22 t^{2}}=4 \quad$ or $\quad t=\frac{2}{g}$
Ex. Particles $P$ and $Q$ of mass $20 \mathrm{gm}$ and $40 \mathrm{gm}$ respectively are simultaneously projected from point $A$ and $B$ on the ground. The initial velocities of $P$ and $Q$ make $45^{\circ}$ and $135^{\circ}$ angles respectively with the horizontal AB as shown in fig. Each particle has an initial speed of $49 \mathrm{~m} / \mathrm{sec}$. The separator $A B$ is $245 \mathrm{~m}$. Both particles travel in the same vertical plane and
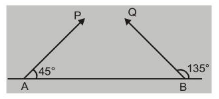undergo a collision. After collision P retraces its path. Determine the position of $Q$ when it hits the ground. How much time after the collision does the particle
$Q$ take to reach the ground? (Take $g=9.8 \mathrm{~m} / \mathrm{s}^{2}$ )
Sol. As the horizontal speed of two particles towards each other is same (u $\cos 45$ ), they will meet at the middle of $A B$, i.e., at distance $(245 / 2)=122.5$ from $A$ toward $B$.
Now as $\mathrm{R}=\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}=\mathrm{R}=\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}}=\frac{49 \times 49 \times 1}{9.8}=245 \mathrm{~m}$
so $A B$ is the range and as the collision takes place at the middle of $A B$, so it is at the highest point of the trajectory.
Now applying conservation of linear momentum at the highest point along horizontal direction keeping in mind, $v_{p}=-u_{p} \cos 45^{\circ}, .$
$20 \times 10^{-3} u \cos 45^{\circ}-40 \times 10^{-3} u \cos 45^{\circ}=-20 \times 10^{-3} u \cos 45^{\circ}+v_{0}(u=49 \mathrm{~m} . / \mathrm{sec} .)$
This give $v_{0}=0$, i.e., after collision, the velocity of $Q$ at highest point is zero. So $Q$ will fall freely
under gravity and will hit the ground in the middle of AB, i.e., $122.5 \mathrm{~m}$ from A towards B.
Now as $\mathrm{H}=\frac{\mathrm{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}=\frac{49 \times 49 \times 1}{2 \times 9.8 \times 2}=\frac{490}{8}=61.25 \mathrm{~m}$
So time taken by $Q$ to reach ground, $t=\sqrt{\frac{2 H}{g}}=\sqrt{\left(\frac{2 \times 490}{8 \times 9.8}\right)}=\frac{5}{\sqrt{2}}=3.536 \mathrm{sec}$
Ex. Is it important in the long jump that how much height you take for jumping.
Sol. It is important in the long jump how high a person jumps.
As $\quad \mathrm{h}=\frac{\mathrm{u}^{2} \sin ^{2} \theta}{2 \mathrm{~g}}$
and $\quad$ range $R=\frac{u^{2} \sin 2 \theta}{g}=\frac{2 h}{\sin ^{2} \theta} \times \sin 2 \theta=4 h \cot \theta$
i.e. the range of jump is determined by initial speed $u$ and angle $\theta$.
or height $h$ and angle of projection $\theta$.
Ex. An object of mass $5 \mathrm{~kg}$ is projected with a velocity of $20 \mathrm{~m} / \mathrm{s}$ at an angle of $60^{\circ}$ to the horizontal. At the highest point of its path the projectile explodes and breaks up into two fragments of masses $1 \mathrm{~kg}$ and $4 \mathrm{~kg}$. The fragments separate horizontally after the explosion. The explosion releases internal energy such that the kinetic energy of the system, at the highest point is doubled. Calculate the separation between the two fragments when they reach the ground. $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^{2}\right)$.
Sol. At the highest point of trajectory applying conservation of linear momentum along horizontal,
$5 \times 20 \cos 60=1 \times v_{1}+4 v_{2}, \quad$ i.e., $v_{1}+4 v_{2}=50$
And by conservation of energy at highest point, according to given condition,
$\left(\frac{1}{2} \times 5 \times 10^{2}\right) \times 2=\frac{1}{2} \times 1 \mathrm{v}_{1}^{2}+\frac{1}{2} 4 \mathrm{v}_{2}^{2}$,
i.e. $\mathrm{v}_{1}^{2}+4 \mathrm{v}_{2}^{2}=1000$
Substituting $v_{1}$ from eqn. (1) in (2),
$\left(50-4 v_{2}\right)^{2}+4 v_{2}^{2}=1000, \quad$ i.e. $v_{2}^{2}-20 v_{2}+75=0$
which on solving gives
$v_{2}=5 \mathrm{~m} / \mathrm{s} \quad$ or $\quad 15 \mathrm{~m} / \mathrm{s}$
So from Equn. (1),
for $\quad v_{2}=5 \mathrm{~m} / \mathrm{s} \quad v_{1}=30 \mathrm{~m} / \mathrm{s}$
and for $v_{2}=15 \mathrm{~m} / \mathrm{s}$ $v_{1}=-10 \mathrm{~m} / \mathrm{s}$
so if both the particle move in same direction,
$v_{\text {rel }}=30-5=25 \mathrm{~m} / \mathrm{s}$
and if both move in opposite direction,
$v_{\text {rel }}=15-(-10)=25 \mathrm{~m} / \mathrm{s}$
i.e., fragments after explosion separate from each other horizontally $25 \mathrm{~m}$ per sec.
Now as time taken by fragments to reach, ground
$\mathrm{t}=\frac{\mathrm{T}}{2}=\frac{\mathrm{u} \sin \theta}{\mathrm{g}}=\frac{20 \times \sqrt{3}}{10 \times 2}=\sqrt{3} \mathrm{~s}$
So the separation between two fragments when they reach the ground
$d=v_{\text {fel }} \times t=25 \times \sqrt{3}=43.3 \mathrm{~m}$
Ex. If a projectile has a constant initial speed and angle of projection, find the relation between the change in the horizontal range due to change in acceleration due to gravity.
Sol. Horizontal range, $R=\frac{u^{2} \sin 2 \theta}{g}$
Differentiating $t$ w.r.t. we have
$\frac{\mathrm{dR}}{\mathrm{dg}}=-\frac{\mathrm{u}^{2}}{\mathrm{~g}^{2}} \sin 2 \theta$ $[\therefore \quad \mathrm{u}$ and $\theta$ are constant $]$
or $\quad \mathrm{dR}=-\frac{\mathrm{u}^{2} \sin 2 \theta}{\mathrm{g}^{2}} \frac{\mathrm{dg}}{\mathrm{g}}=-\mathrm{R} \frac{\mathrm{dg}}{\mathrm{g}}$
or $\quad \frac{\mathrm{dR}}{\mathrm{R}}=-\frac{\mathrm{dg}}{\mathrm{g}}$
Also Read
JEE Physics Notes
To watch Free Learning Videos on JEE by Kota’s top IITian Faculties Install the eSaral App