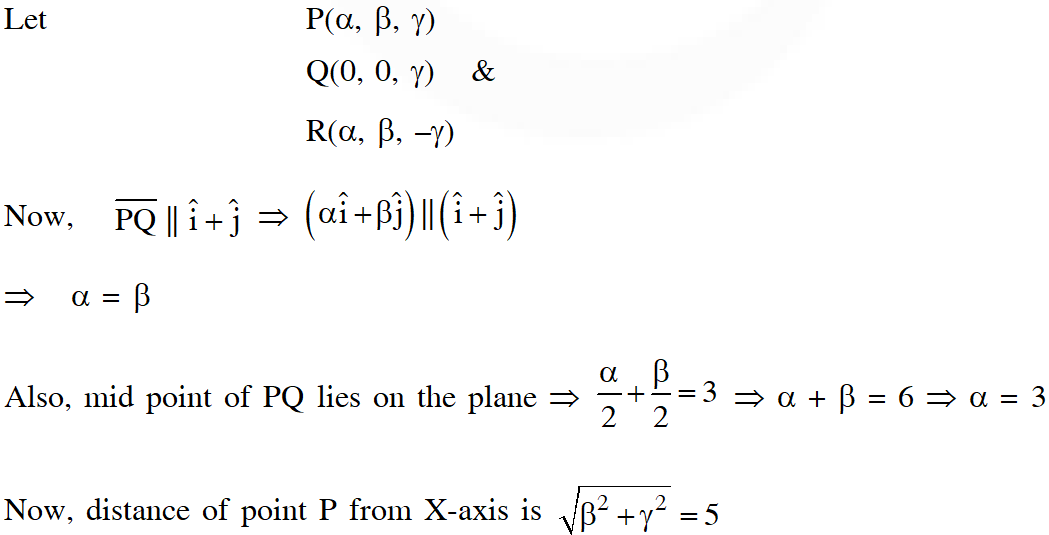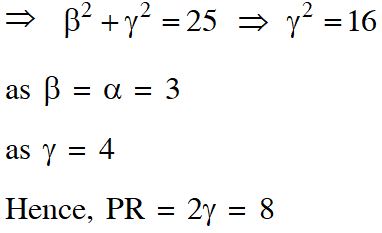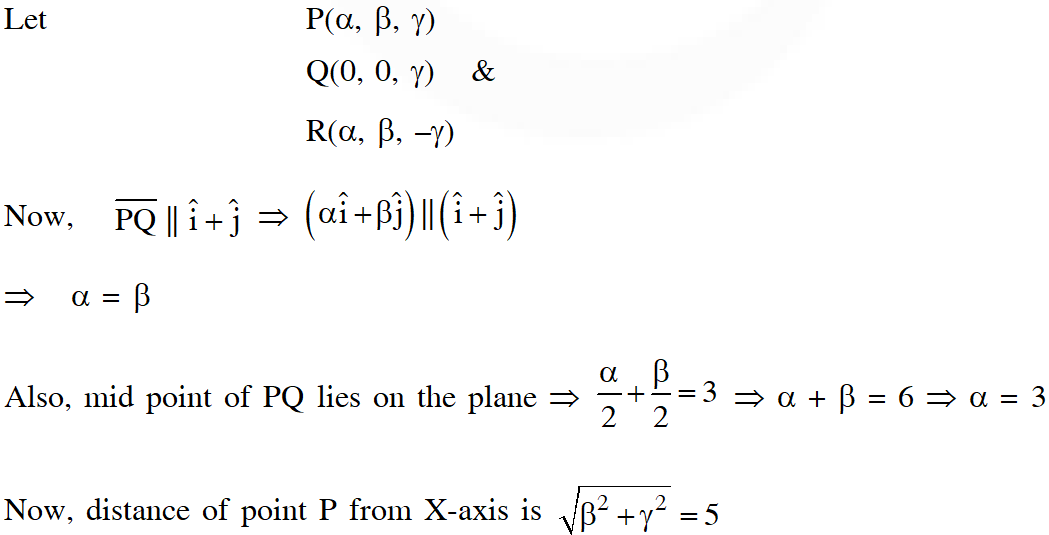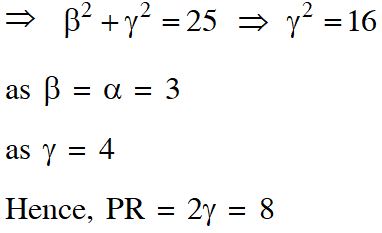JEE Advanced Previous Year Questions of Math with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral also provides complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. (A) Let $\mathrm{P}(3,2,6)$ be a point in space and $\mathrm{Q}$ be a point on the line $\overrightarrow{\mathrm{r}}=(\hat{\mathrm{i}}-\hat{\mathrm{j}}+2 \hat{\mathrm{k}})+\mu(-3 \hat{\mathrm{i}}+\hat{\mathrm{j}}+5 \hat{\mathrm{k}}) .$ Then the value of $\mu$ for which the vector $\overline{\mathrm{PQ}}$ is parallel to the plane $x-4 y+3 z=1$ is -
(A) $\frac{1}{4}$
(B) $-\frac{1}{4}$
(C) $\frac{1}{8}$
(D) $-\frac{1}{8}$
(B) A line with positive direction cosines passes through the point P (2, –1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals –
(A) 1
(B) $\sqrt{2}$
(C) $\sqrt{3}$
(D) 2
(C) Let $(\mathrm{x}, \mathrm{y}, \mathrm{z})$ be points with integer coordinates satisfying the system of homogeneous equations $: 3 x-y-z=0 ;-3 x+z=0 ;-3 x+2 y+z=0 .$ Then the number of such points for which $\mathrm{x}^{2}+\mathrm{y}^{2}+\mathrm{z}^{2} \leq 100$ is
[JEE 2009, 3+3+4]
Ans. ( (a) $A ;(b) C ;(c) 7$ )
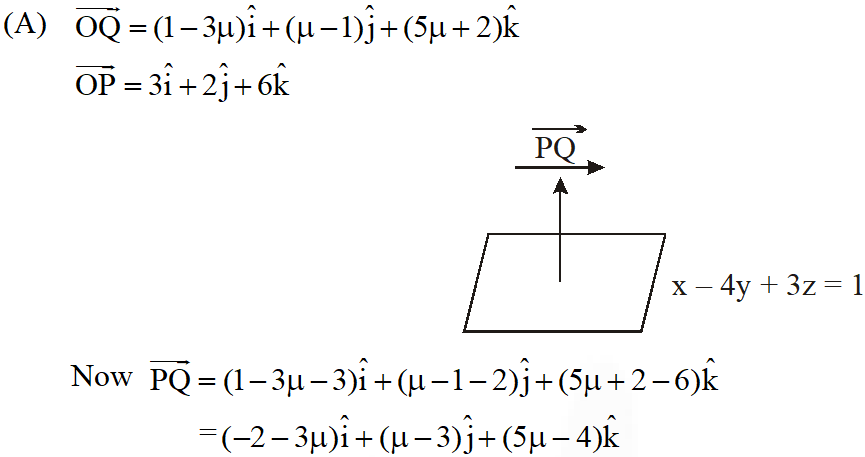
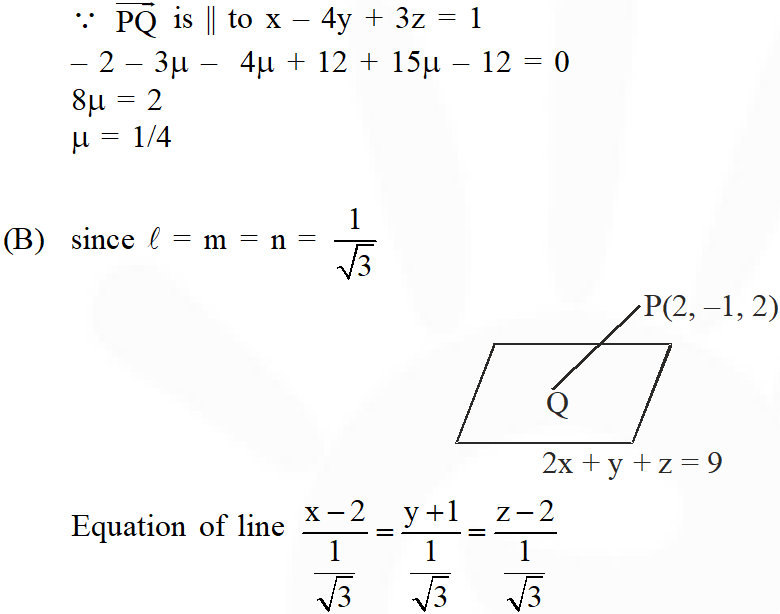
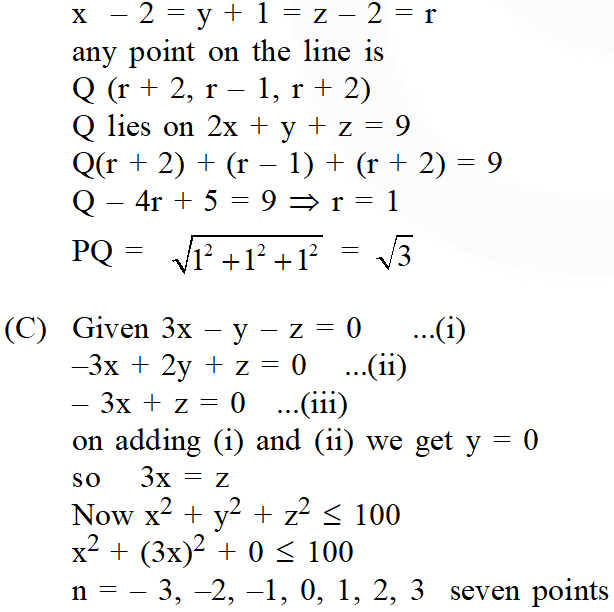
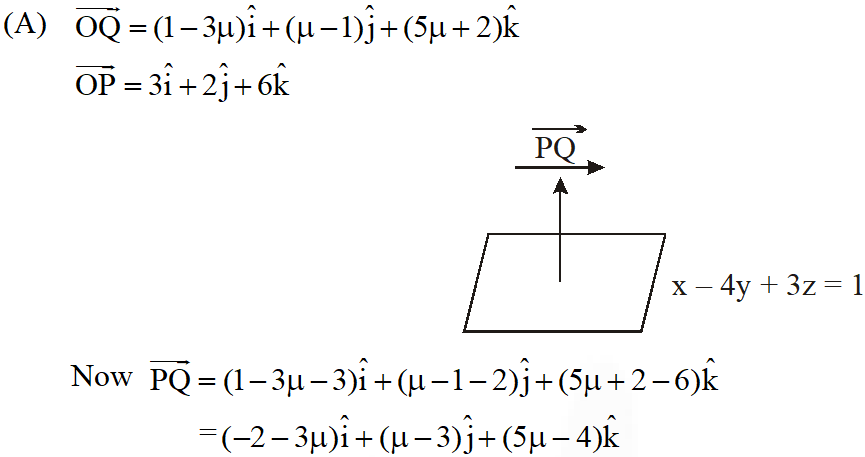
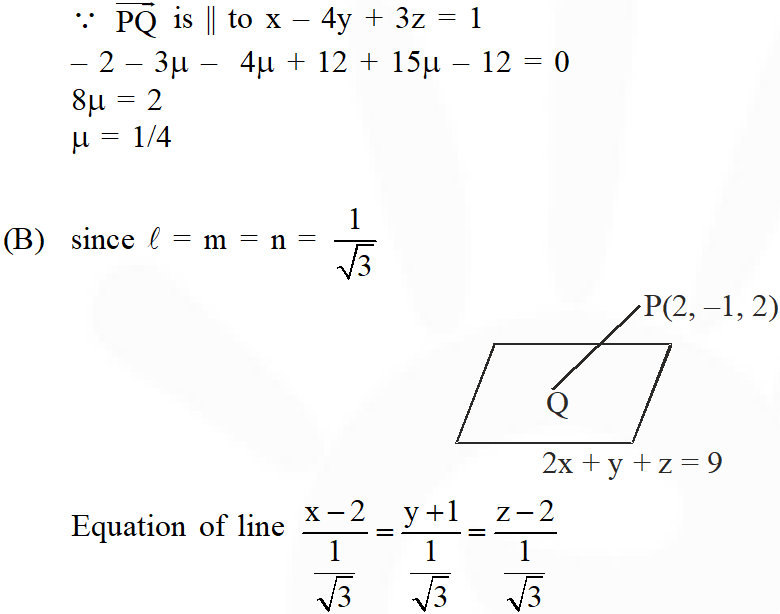
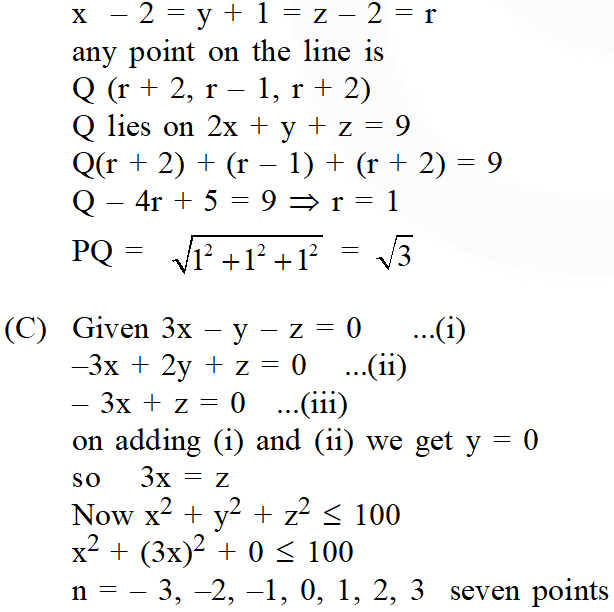
Q. (A) Equation of the plane containing the straight line $\frac{\mathrm{x}}{2}=\frac{\mathrm{y}}{3}=\frac{\mathrm{z}}{4}$ and perpendicular to the plane containing the straight lines $\frac{x}{3}=\frac{y}{4}=\frac{z}{2}$ and $\frac{x}{4}=\frac{y}{2}=\frac{z}{3}$
(A) x + 2y – 2z = 0
(B) 3x + 2y – 2z = 0
(C) x – 2y + z = 0
(D) 5x + 2y – 4z = 0
(B) If the distance of the point $\mathrm{P}(1,-2,1)$ from the plane $\mathrm{x}+2 \mathrm{y}-2 \mathrm{z}=\alpha$ where $\alpha>0,$ is $5,$ then the foot of the perpendicular from $P$ to the plane is-
(A) $\left(\frac{8}{3}, \frac{4}{3},-\frac{7}{3}\right)$
(B) $\left(\frac{4}{3},-\frac{4}{3}, \frac{1}{3}\right)$
(C) $\left(\frac{1}{3}, \frac{2}{3}, \frac{10}{3}\right)$
(D) $\left(\frac{2}{3},-\frac{1}{3}, \frac{5}{2}\right)$
(C) If the distance between the plane Ax – 2y + z = d and the plane containing the lines $\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}$ and $\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}$ is $\sqrt{6},$ then $|d|$ is
(D) Match the statements in Column-I with the values in Column-II.
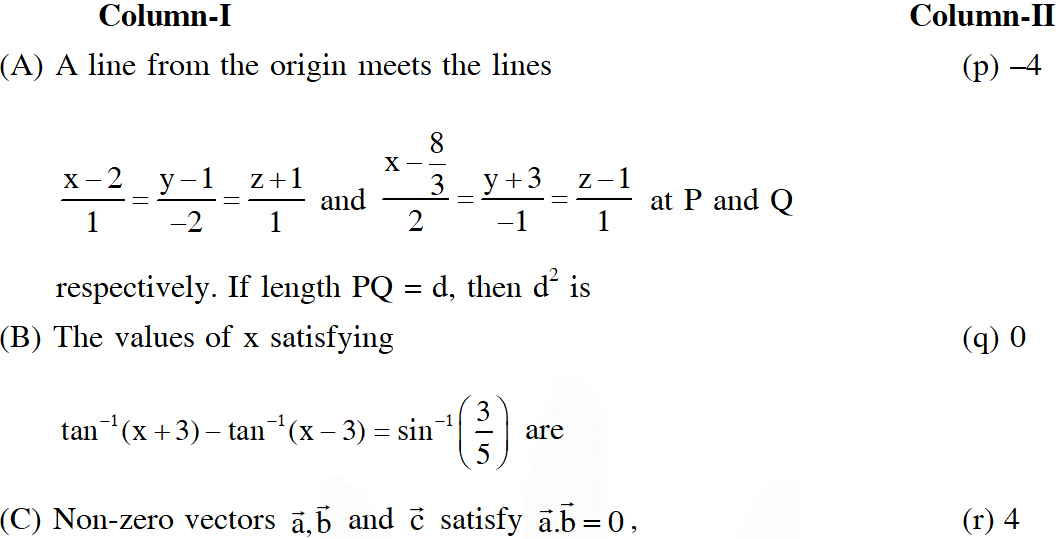
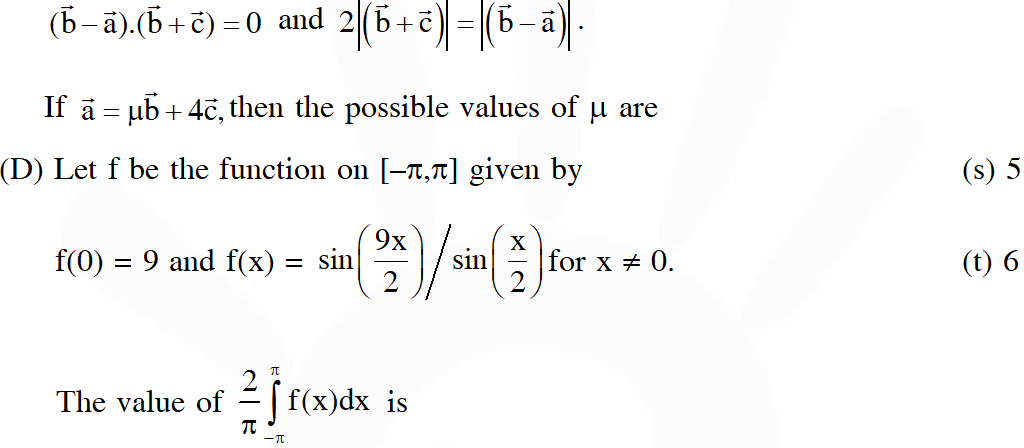[JEE 2010, 3+5+3+(2+2+2+2)]
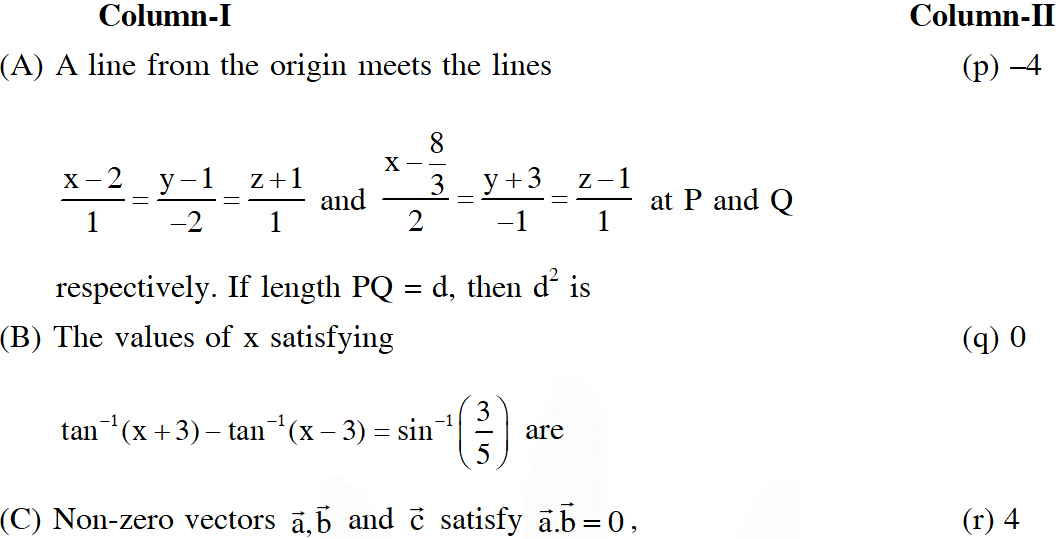
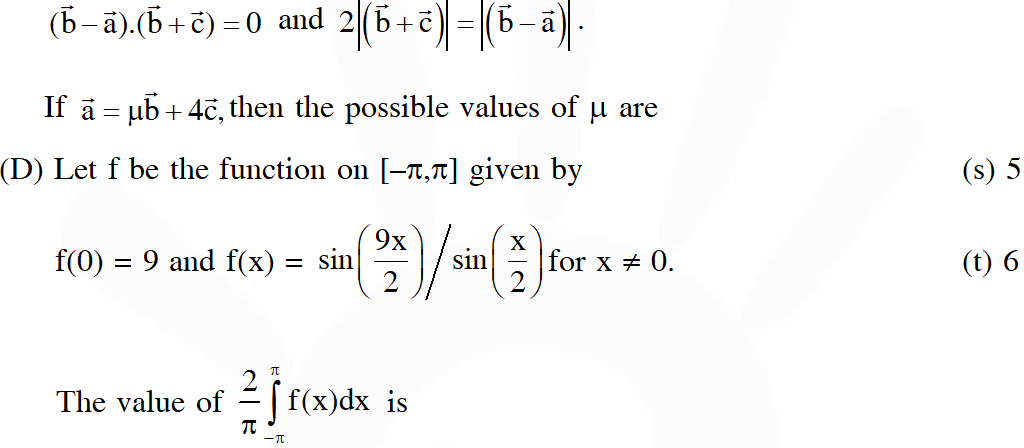[JEE 2010, 3+5+3+(2+2+2+2)]
Ans. ((A) $\mathrm{C} ;(\mathrm{B}) \mathrm{A} ;(\mathrm{C}) 6 ;(\mathrm{D})(\mathrm{A}) \mathrm{t}(\mathrm{B}) \mathrm{p}, \mathrm{r}(\mathrm{C}) \mathrm{q}(\mathrm{D}) \mathrm{r}$ )
(a) Normal vector to the plane containing the
lines $\frac{x}{3}=\frac{y}{4}=\frac{z}{2}$ and $\frac{x}{4}=\frac{y}{2}=\frac{z}{3}$ is
$\hat{n}=\left|\begin{array}{lll}{\hat{i}} & {\hat{j}} & {\hat{k}} \\ {3} & {4} & {2} \\ {4} & {2} & {3}\end{array}\right|=8 \hat{i}-\hat{j}-10 \hat{k}$
Let direction ratios of required plane be a, b, c.
Now 8a – b – 10c = 0
and $2 \mathrm{a}+3 \mathrm{b}+4 \mathrm{c}=0\left(\because \text { plane contains the line } \frac{\mathrm{x}}{2}=\frac{\mathrm{y}}{3}=\frac{\mathrm{z}}{4}\right)$
$\Rightarrow \frac{a}{1}=\frac{b}{-2}=\frac{c}{1}$
$\cdot$ plane contains the line, which passes through origin, hence origin lies on a plane.
$\Rightarrow$ equation of required plane is $x-2 y+z=0$
(b) $\quad \because \quad\left|\frac{1-4-2-\alpha}{3}\right|=5$
$\Rightarrow \alpha=10,-20$
$\Rightarrow \alpha=10 \because \alpha>0$
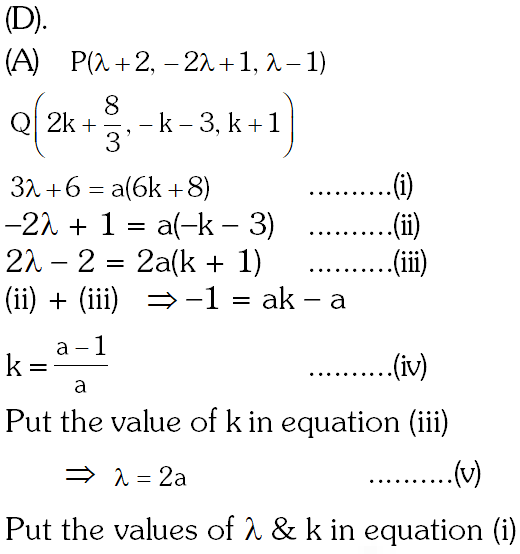
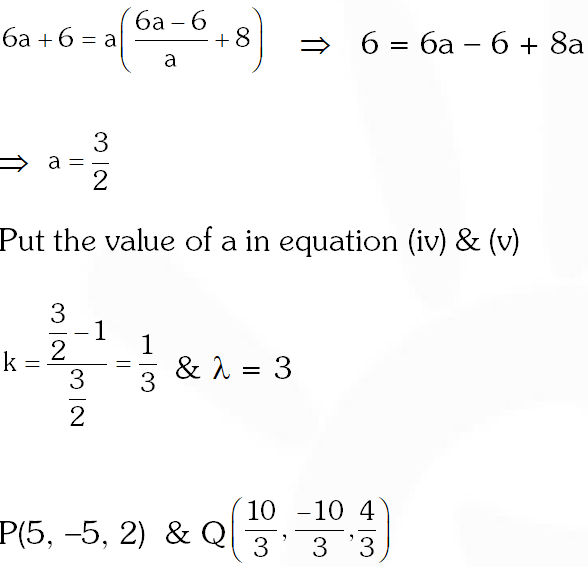
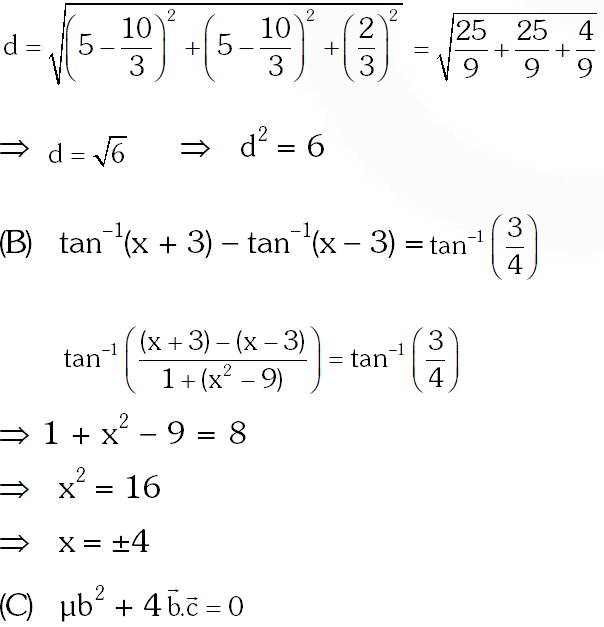
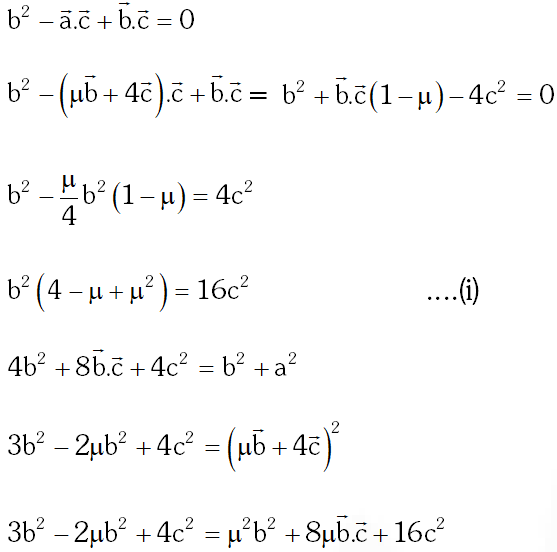
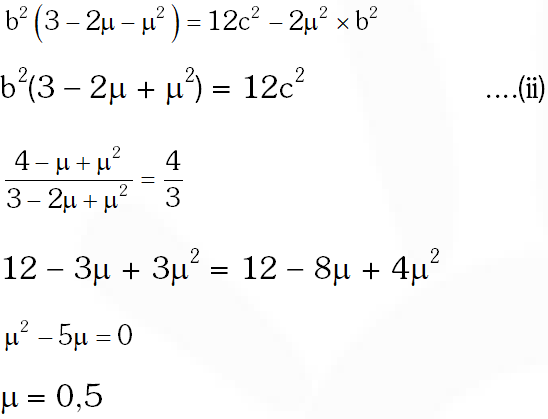
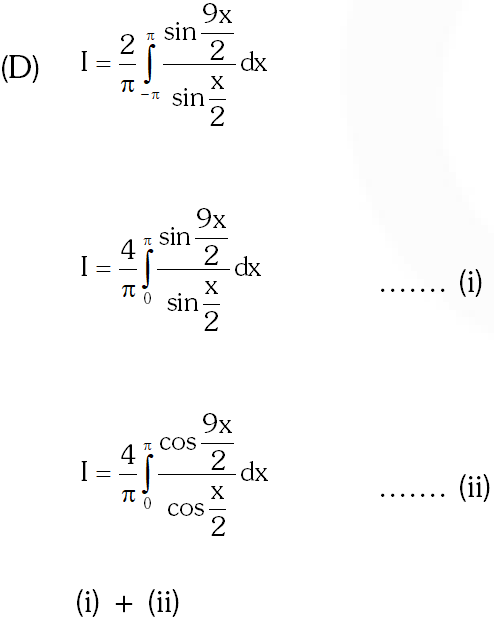
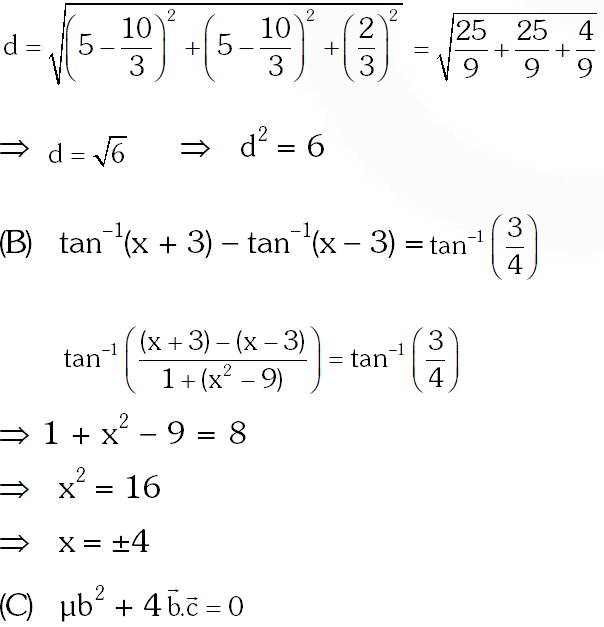
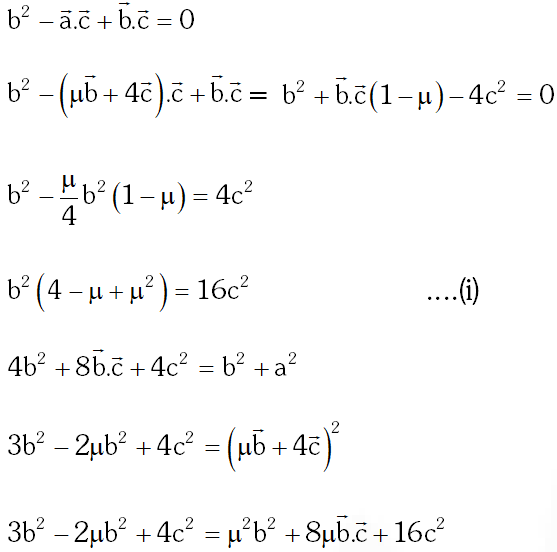
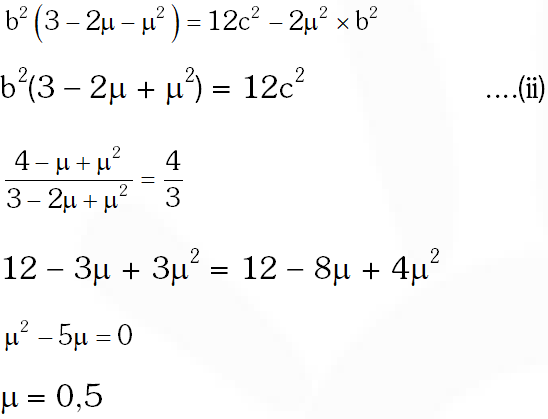
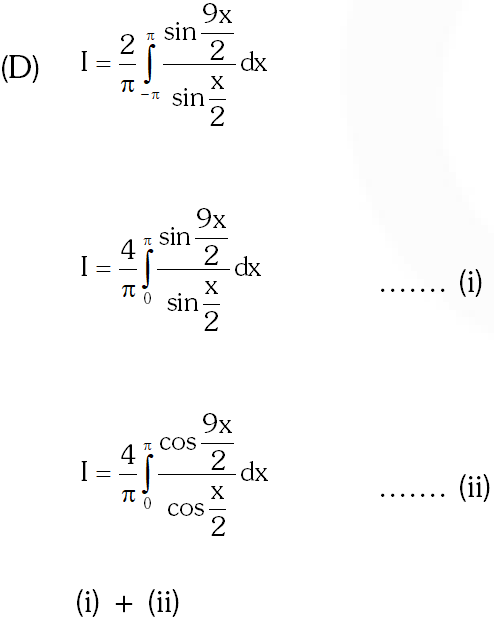
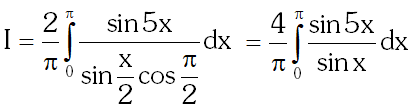
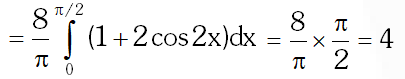
Q. (A) The point P is the intersection of the straight line joining the points Q(2,3,5) and R(1,–1,4) with the plane 5x – 4y – z = 1. If S is the foot of the perpendicular drawn from the point T(2,1,4) to QR, then the length of the line segment PS is –
(A) $\frac{1}{\sqrt{2}}$
(B) $\sqrt{2}$
(C) 2
(D) $2 \sqrt{2}$
(B) The equation of a plane passing through the line of intersection of the planes x + 2y $+3 \mathrm{z}=2$ and $\mathrm{x}-\mathrm{y}+\mathrm{z}=3$ and at a distance $\frac{2}{\sqrt{3}}$ from the point $(3,1,-1)$ is
(A) $5 x-11 y+z=17$
(B) $\sqrt{2} x+y=3 \sqrt{2}-1$
(C) $x+y+z=\sqrt{3}$
(D) $x-\sqrt{2} y=1-\sqrt{2}$
(C) If the straight lines $\frac{x-1}{2}=\frac{y+1}{k}=\frac{z}{2}$ and $\frac{x+1}{5}=\frac{y+1}{2}=\frac{z}{k}$ are coplanar, then the plane(s) containing these two lines is(are)
(A) y + 2z = –1
(B) y + z = –1
(C) y – z = –1
(D) y – 2z = –1
[JEE 2012, 3+3+4]
Ans. ((a) $A ;(b) A ;(c) B, C$)
(a) Line QR :
$\frac{x-2}{1}=\frac{y-3}{4}=\frac{z-5}{1}=\lambda$
Any point on line QR :
$(\lambda+2,4 \lambda+3, \lambda+5)$
$\therefore$ Point of intersection with plane :
$5 \lambda+10-16 \lambda-12-\lambda-5=1$
$\Rightarrow \lambda=-\frac{2}{3}$
$\therefore \mathrm{P}\left(\frac{4}{3}, \frac{1}{3}, \frac{13}{3}\right)$
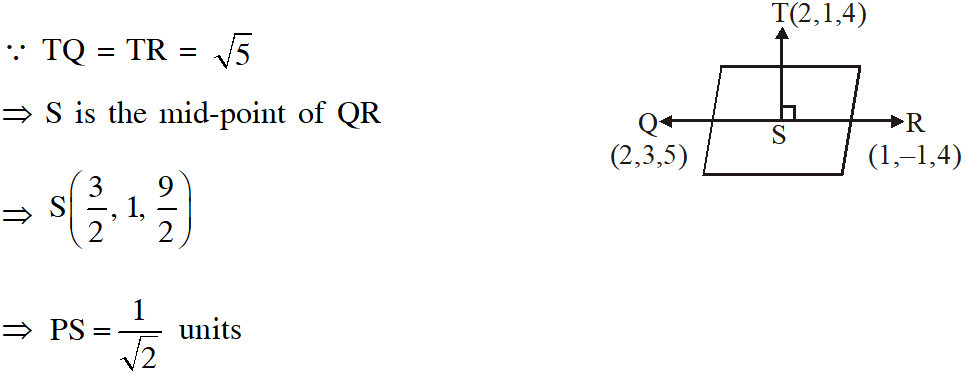
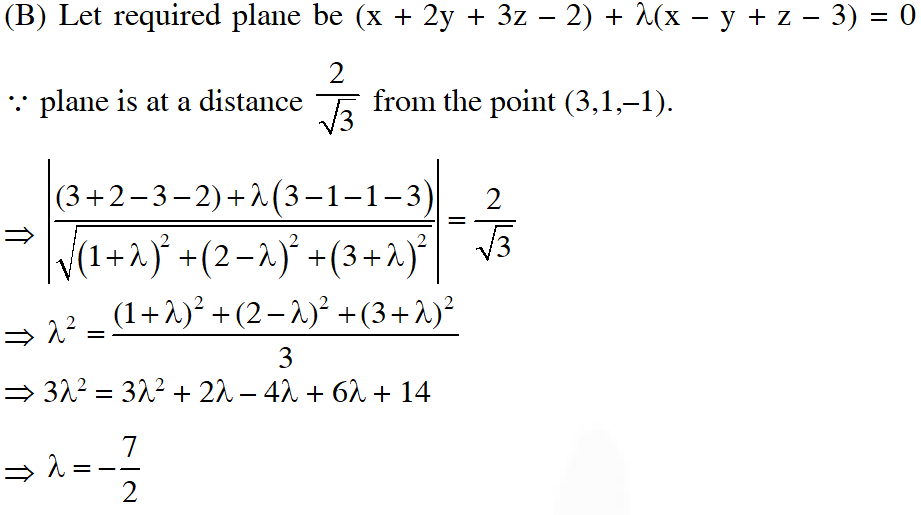
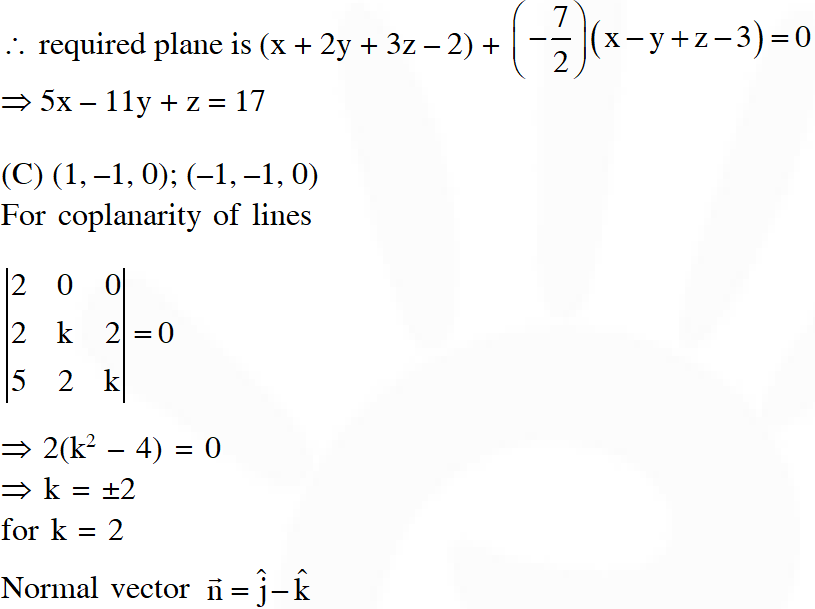
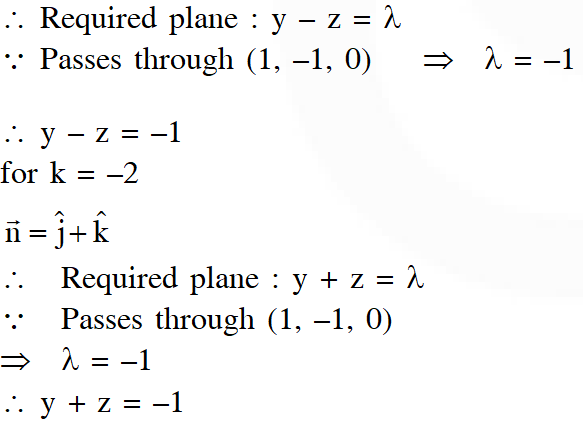
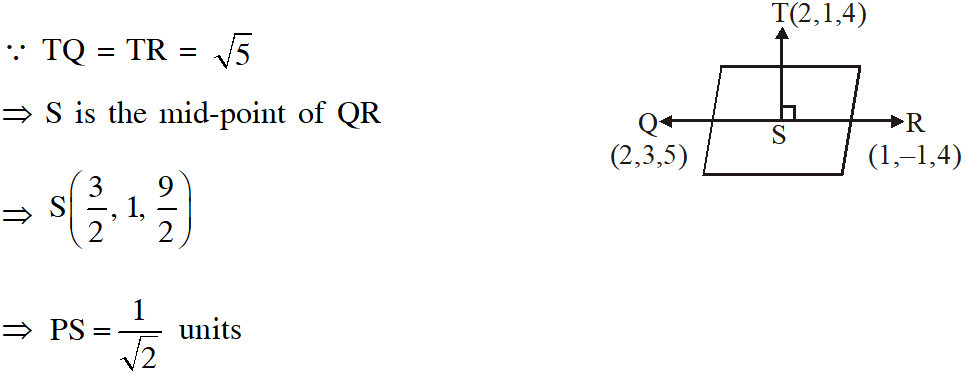
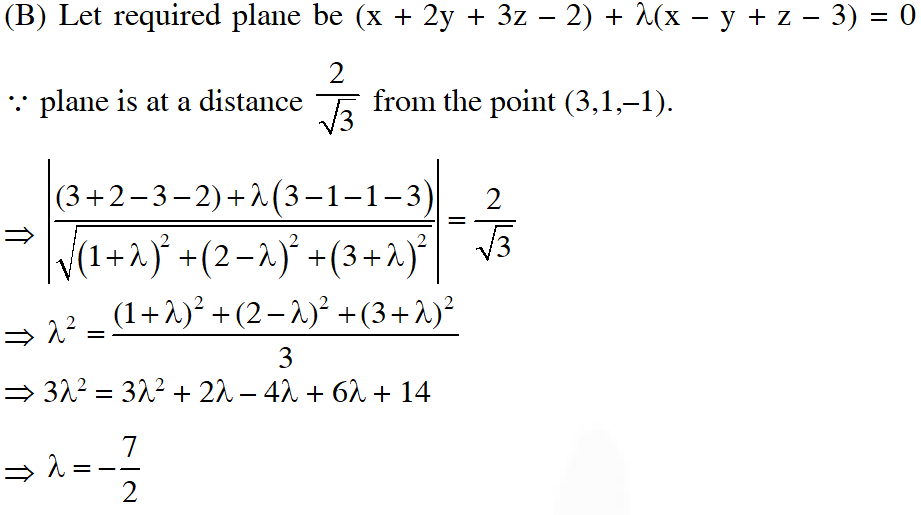
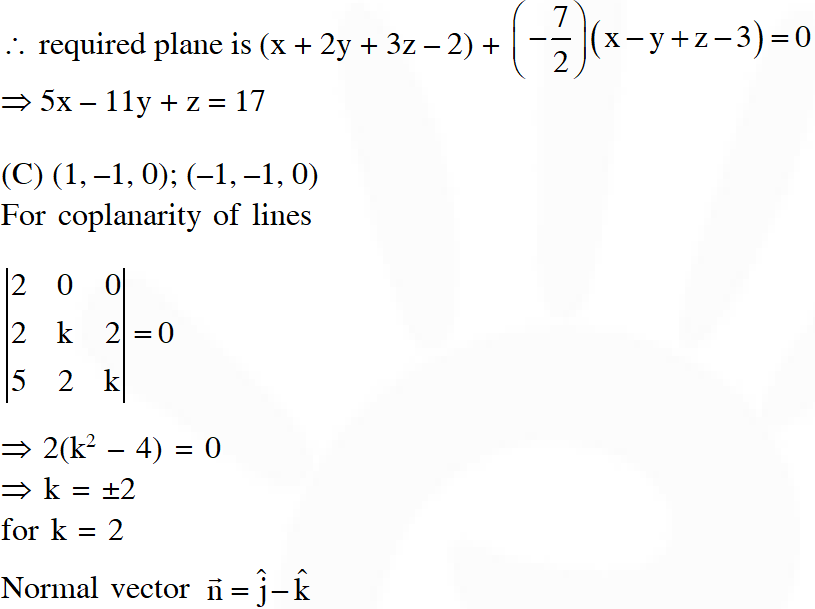
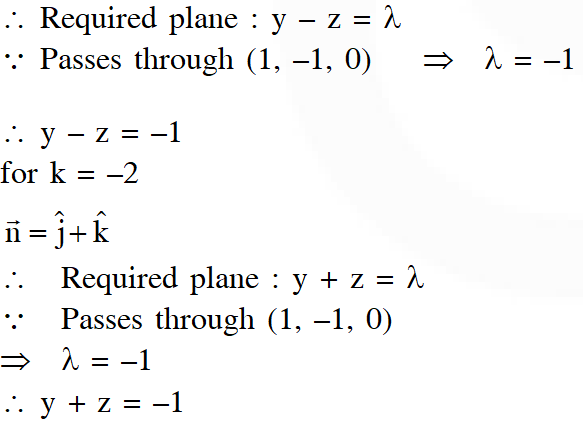
Q. Perpendiculars are drawn from points on the line $\frac{x+2}{2}=\frac{y+1}{-1}=\frac{z}{3}$ to the plane $x$ $+\mathrm{y}+\mathrm{z}=3 .$ The feet of perpendiculars lie on the line
(A) $\frac{x}{5}=\frac{y-1}{8}=\frac{z-2}{-13}$
(B) $\frac{x}{2}=\frac{y-1}{3}=\frac{z-2}{-5}$
(C) $\frac{x}{4}=\frac{y-1}{3}=\frac{z-2}{-7}$
(D) $\frac{x}{2}=\frac{y-1}{-7}=\frac{z-2}{5}$
[JEE-Advanced 2013, 2]
Ans. (D)
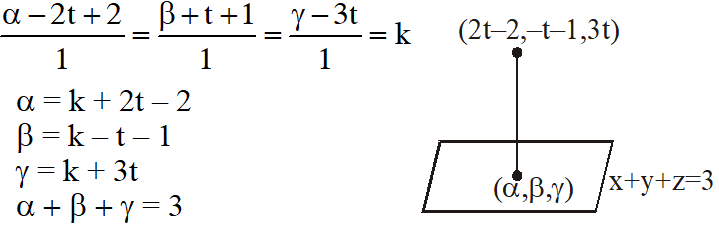
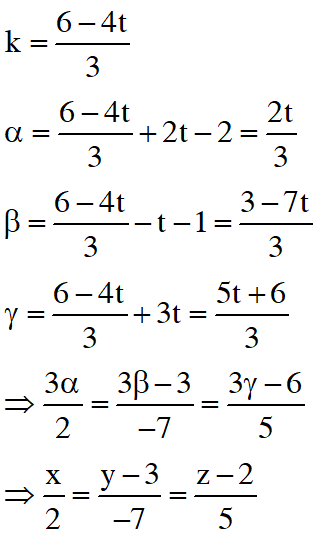
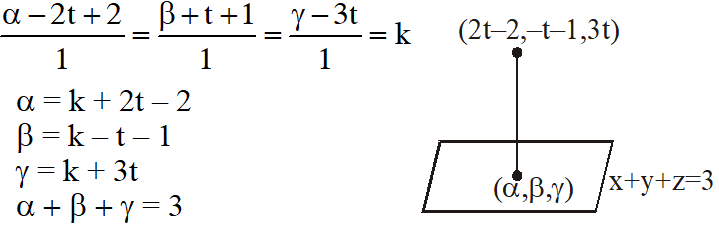
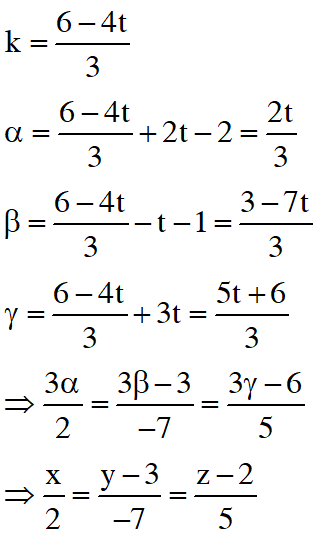
Q. A line $\ell$ passing through the origin is perpendicular to the lines
$\ell_{1}:(3+\mathrm{t}) \hat{\mathrm{i}}+(-1+2 \mathrm{t}) \hat{\mathrm{j}}+(4+2 \mathrm{t}) \hat{\mathrm{k}},-\infty<\mathrm{t}<\infty$
$\ell_{2}:(3+2 s) \hat{\mathrm{i}}+(3+2 \mathrm{s}) \hat{\mathrm{j}}+(2+\mathrm{s}) \hat{\mathrm{k}},-\infty<\mathrm{s}<\infty$ Then, the coordinate(s) of the point(s) on $\ell_{2}$
at a distance of $\sqrt{17}$ from the point of intersection of $\ell$ and $\ell_{1}$ is (are) –
(A) $\left(\frac{7}{3}, \frac{7}{3}, \frac{5}{3}\right)$
(B) (–1,–1,0)
(C) (1,1,1)
(D) $\left(\frac{7}{9}, \frac{7}{9}, \frac{8}{9}\right)$
[JEE-Advanced 2013, 4, (–1)]
Ans. (B,D)
Q. Two lines $L_{1}: x=5, \frac{y}{3-\alpha}=\frac{z}{-2}$ and $L_{2}: x=\alpha, \frac{y}{-1}=\frac{z}{2-\alpha}$ are coplanar. Then $\alpha$ can take value(s)
(A) 1 (B) 2 (C) 3 (D) 4
[JEE-Advanced 2013, 3, (–1)]
Ans. (A,D)
$\mathrm{L}_{1}: \frac{\mathrm{x}-5}{0}=\frac{\mathrm{y}}{3-\alpha}=\frac{\mathrm{z}}{-2}$
$\mathrm{L}_{2}: \frac{\mathrm{x}-\alpha}{0}=\frac{\mathrm{y}}{-1}=\frac{\mathrm{z}}{2-\alpha}$
for lines to be coplanar
$\left|\begin{array}{ccc}{5-\alpha} & {0} & {0} \\ {0} & {3-\alpha} & {-2} \\ {0} & {-1} & {2-\alpha}\end{array}\right|=0$
$\Rightarrow \quad(5-\alpha)((3-\alpha)(2-\alpha)-2)=0$
$\Rightarrow \quad(5-\alpha)\left(\alpha^{2}-5 \alpha+4\right)=0$
$\Rightarrow \quad \alpha=1,4,5$
Q. Consider the lines $\mathrm{L}_{1}: \frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}}{-1}=\frac{\mathrm{z}+3}{1}, \mathrm{L}_{2}: \frac{\mathrm{x}-4}{1}=\frac{\mathrm{y}+3}{1}=\frac{\mathrm{z}+3}{2}$ and the planes $\mathrm{P}_{1}: 7 \mathrm{x}+\mathrm{y}+2 \mathrm{z}=3, \mathrm{P}_{2}: 3 \mathrm{x}+5 \mathrm{y}-6 \mathrm{z}=4 .$ Let $\mathrm{ax}+\mathrm{by}+\mathrm{cz}=\mathrm{d}$ be the
equation of the plane passing through the point of intersection of lines $L_{1}$ and $\mathrm{L}_{2}$ and perpendicular to planes $\mathrm{P}_{1}$ and $\mathrm{P}_{2} .$ Match List-I with List-II and select the correct answer using the code given below the lists.
[JEE-Advanced 2013, 3, (–1)]
[JEE-Advanced 2013, 3, (–1)]
Ans. (A)
For point of intersection of $L_{1}$ and $L_{2}$
$\left\{\begin{array}{l}{2 \lambda+1=\mu+4} \\ {-\lambda=\mu-3} \\ {\lambda-3=2 \mu-3}\end{array}\right.$
$\Rightarrow \mu=1$
$\Rightarrow$ point of intersction is $(5,-2,-1)$
Now, vector normal to the plane is $\overrightarrow{\mathrm{n}}_{1} \times \overrightarrow{\mathrm{n}}_{2}=\left|\begin{array}{ccc}{\hat{\mathrm{i}}} & {\hat{\mathrm{j}}} & {\hat{\mathrm{k}}} \\ {7} & {1} & {2} \\ {3} & {5} & {-6}\end{array}\right|$
$=-16(\hat{i}-3 \hat{j}-2 \hat{k})$
Let equation of required plane be $x-3 y-2 z=\alpha$
$\because$ it passes through $(5,-2,-1)$
$\therefore \alpha=13$
$\Rightarrow$ equation of plane is $x-3 y-2 z=13$
Q. From a point $\mathrm{P}(\lambda, \lambda, \lambda),$ perpendiculars $\mathrm{PQ}$ and $\mathrm{PR}$ are drawn respectively on the lines $\mathrm{y}=$ $\mathrm{x}, \mathrm{z}=1$ and $\mathrm{y}=-\mathrm{x}, \mathrm{z}=-1 .$ If $\mathrm{P}$ is such that $\angle \mathrm{QPR}$ is a right angle, then the possible value(s) of $\lambda$ is (are)
(A) $\sqrt{2}$ (B) 1 (C) –1 (D) $-\sqrt{2}$
[JEE(Advanced)-2014, 3]
Ans. (C)
Line $\mathrm{L}_{1}$ given by $\mathrm{y}=\mathrm{x} ; \mathrm{z}=1$ can be expressed as
$\mathrm{L}_{1}: \frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{1}=\frac{\mathrm{z}-1}{0}$
Similarly $\mathrm{L}_{2}(\mathrm{y}=-\mathrm{x} ; \mathrm{z}=-1)$ can be expressed as
$\mathrm{L}_{2}: \frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{-1}=\frac{\mathrm{z}+1}{0}$
Let any point $\mathrm{Q}(\alpha, \alpha, 1)$ on $\mathrm{L}_{1}$ and $\mathrm{R}(\beta,-\beta,-1)$ on $\mathrm{L}_{2}$
Given that $\mathrm{PQ}$ is perpendicular to $\mathrm{L}_{1}$
$\Rightarrow(\lambda-\alpha) .1+(\lambda-\alpha) \cdot 1+(\lambda-1) \cdot 0=0 \Rightarrow \lambda=\alpha$
$\therefore \mathrm{Q}(\lambda, \lambda, 1)$
Similarly PR is perpendicular to L $_{2}$ $(\lambda-\beta) \cdot 1+(\lambda+\beta)(-1)+(\lambda+1) \cdot 0=0 \Rightarrow \beta=0$
$\therefore \mathrm{R}(0,0,-1)$
Now as given
$\Rightarrow \overrightarrow{\mathrm{PR}} \cdot \overrightarrow{\mathrm{PQ}}=0$
$0 . \lambda+0 . \lambda+(\lambda-1)(\lambda+1)=0$
$\lambda \neq 1$ as $\mathrm{P} \& \mathrm{Q}$ are different points
$\Rightarrow \lambda=-1$
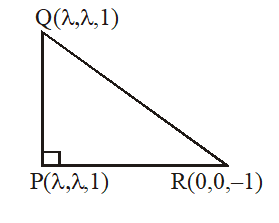
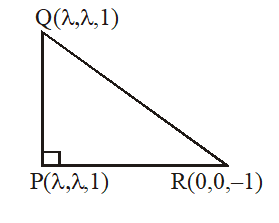
Q. In $\mathbb{D}^{3},$ consider the planes $P_{1}: y=0$ and $P_{2}: x+z=1 .$ Let $P_{3}$ be a plane, different from $\mathrm{P}_{1}$ and $\mathrm{P}_{2},$ which passes through the intersection of $\mathrm{P}_{1}$ and $\mathrm{P}_{2} .$ If the distance of the point $(0,1,0)$ from $P_{3}$ is 1 and the distance of a point $(\alpha, \beta, \gamma)$ from $P_{3}$ is $2,$ then which of the following relations is (are) true?
(A) $2 \alpha+\beta+2 \gamma+2=0$
(B) $2 \alpha-\beta+2 \gamma+4=0$
(C) $2 \alpha+\beta-2 \gamma-10=0$
(D) $2 \alpha-\beta+2 \gamma-8=0$
[JEE 2015, 4M, –2M]
Ans. (B,D)
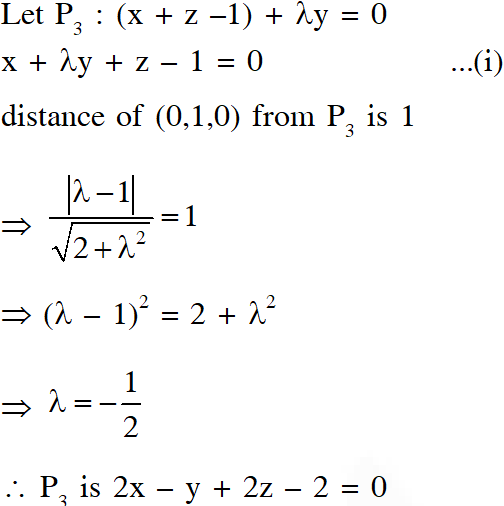
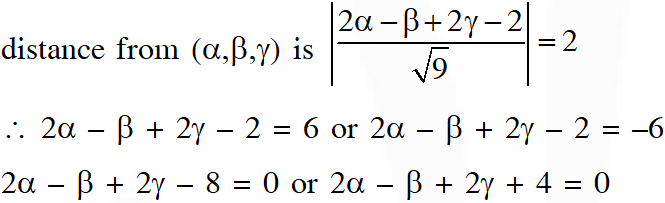
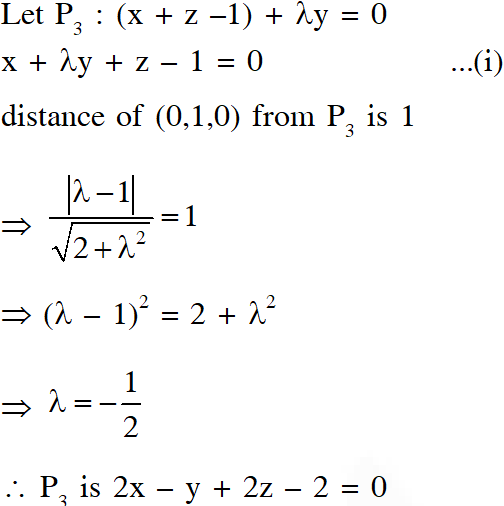
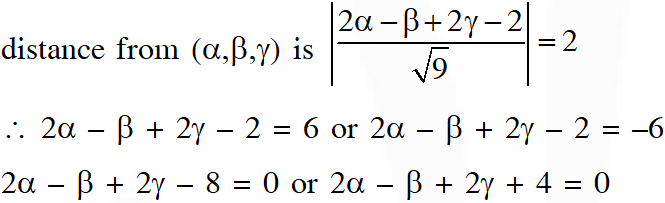
Q. In $\square^{3},$ let $L$ be a straight line passing through the origin. Suppose that all the points on $L$ are at a constant distance from the two planes $P_{1}: x+2 y-z+1=0$ and $P_{2}: 2 x-y+$ $\mathrm{z}-1=0 .$ Let $\mathrm{M}$ be the locus of the feet of the perpendiculars drawn from the points on L to the plane $P_{1} .$ Which of the following points lie(s) on M?
[JEE 2015, 4M, –2M]
[JEE 2015, 4M, –2M]
Ans. (A,B)
Straight line 'L' is parallel to line of intersection of plane $\mathrm{P}_{1} \&$ plane $\mathrm{P}_{2}$
$\therefore$ Equation of line $^{\prime} \mathbf{L}^{\prime}$ is
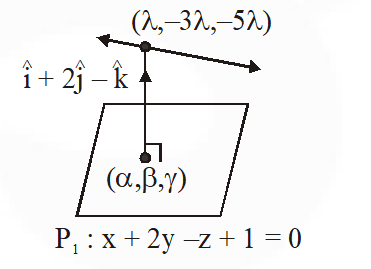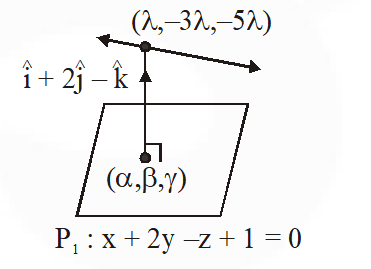$\frac{x}{1}=\frac{y}{-3}=\frac{z}{-5}=\lambda$
$\frac{\alpha-\lambda}{1}=\frac{\beta+3 \lambda}{2}=\frac{\gamma+5 \lambda}{-1}=\mathrm{k}$
$\left.\begin{array}{l}{\alpha=\mathrm{k}+\lambda} \\ {\beta=2 \mathrm{k}-3 \lambda} \\ {\mathrm{y}=-\mathrm{k}-5 \lambda}\end{array}\right\}$ ...(1)
satisfying in plane $\mathrm{P}_{1}$
$\mathrm{k}+\lambda+4 \mathrm{k}-6 \lambda+\mathrm{k}+5 \lambda+1=0$
$6 k=-1$
putting in ( 1) required locus is
$\mathrm{x}=-\frac{1}{6}+\lambda$
$y=-\frac{1}{3}-3 \lambda$
$z=\frac{1}{6}-5 \lambda$
Now check the options.
$\frac{x}{1}=\frac{y}{-3}=\frac{z}{-5}=\lambda$
$\frac{\alpha-\lambda}{1}=\frac{\beta+3 \lambda}{2}=\frac{\gamma+5 \lambda}{-1}=\mathrm{k}$
$\left.\begin{array}{l}{\alpha=\mathrm{k}+\lambda} \\ {\beta=2 \mathrm{k}-3 \lambda} \\ {\mathrm{y}=-\mathrm{k}-5 \lambda}\end{array}\right\}$ ...(1)
satisfying in plane $\mathrm{P}_{1}$
$\mathrm{k}+\lambda+4 \mathrm{k}-6 \lambda+\mathrm{k}+5 \lambda+1=0$
$6 k=-1$
putting in ( 1) required locus is
$\mathrm{x}=-\frac{1}{6}+\lambda$
$y=-\frac{1}{3}-3 \lambda$
$z=\frac{1}{6}-5 \lambda$
Now check the options.
Q. Consider a pyramid OPQRS located in the first octant $(\mathrm{x} \geq 0, \mathrm{y} \geq 0, \mathrm{z} \geq 0)$ with $\mathrm{O}$ as origin, and OP and OR along the x-axis and the y-axis, respectively. The base OPQR of the pyramid is a square with $\mathrm{OP}=3 .$ The point $\mathrm{S}$ is directly above the mid-point $\mathrm{T}$ of diagonal OQ such that TS $=3 .$ Then-
(A) the acute angle between $\mathrm{OQ}$ and $\mathrm{OS}$ is $\frac{\mathrm{K}}{3}$
(B) the equaiton of the plane containing the triangle $\mathrm{OQS}$ is $\mathrm{x}-\mathrm{y}=0$
(C) the length of the perpendicular from $P$ to the plane containing the triangle OQS is $\frac{3}{\sqrt{2}}$
(D) the perpendicular distance from $\mathrm{O}$ to the straight line containing RS is $\sqrt{\frac{15}{2}}$
[JEE(Advanced) 2016]
Ans. (B,C,D)
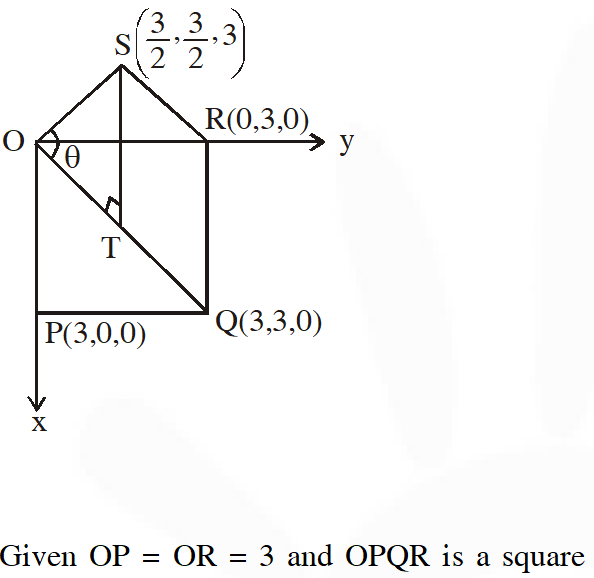
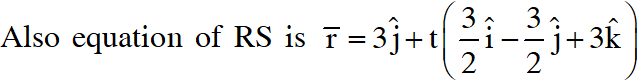
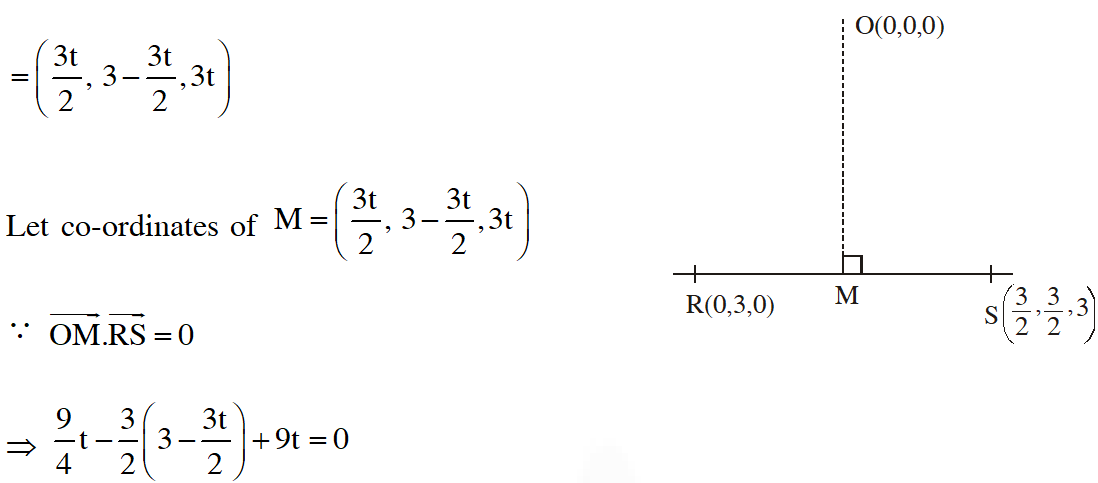
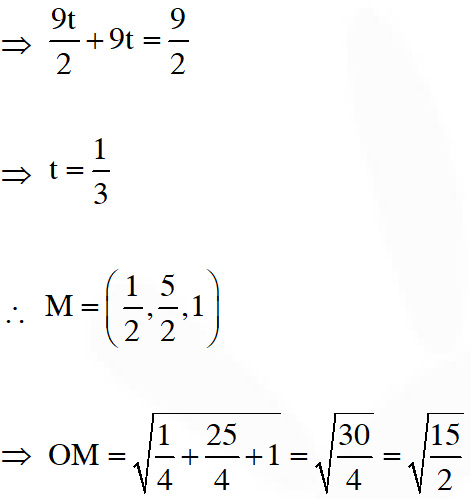
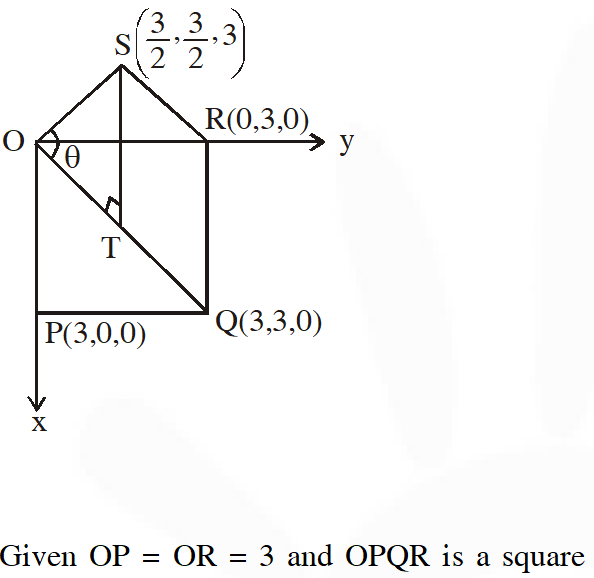
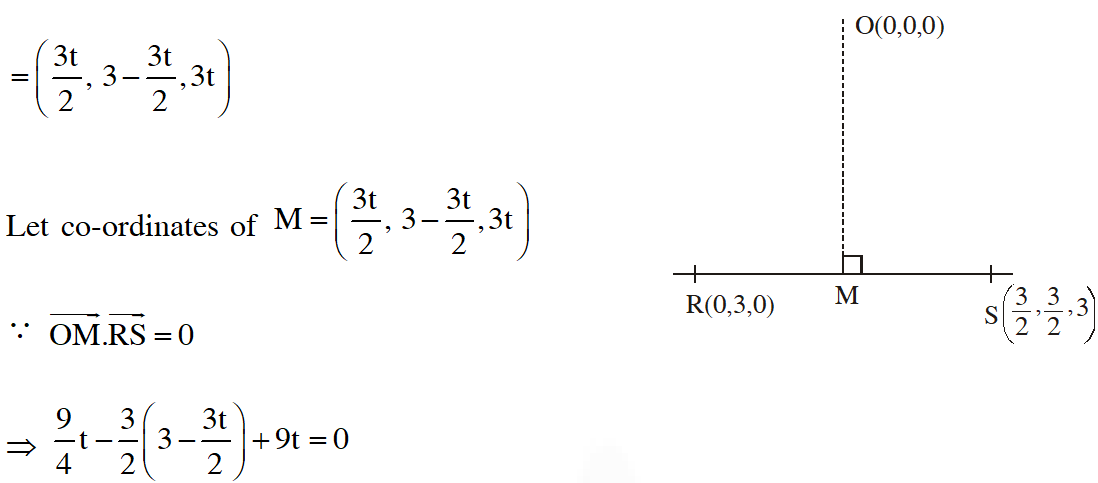
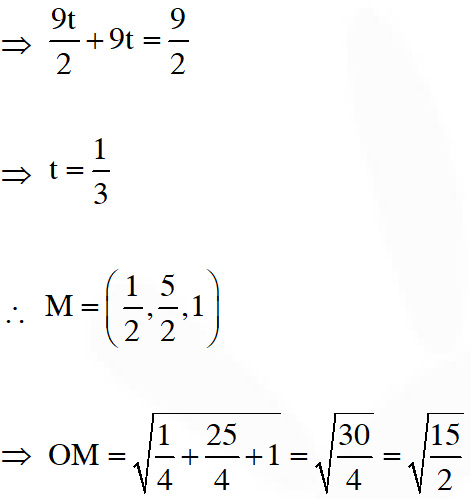
Q. Let $P$ be the image of the point $(3,1,7)$ with respect to the plane $x-y+z=3 .$ Then the equation of the plane passing through $\mathrm{P}$ and containing the straight line $\frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{2}=\frac{\mathrm{z}}{1}$ is
(A) x + y – 3z = 0
(B) 3x + z = 0
(C) x – 4y + 7z = 0
(D) 2x – y = 0
[JEE(Advanced) 2016]
Ans. (C)
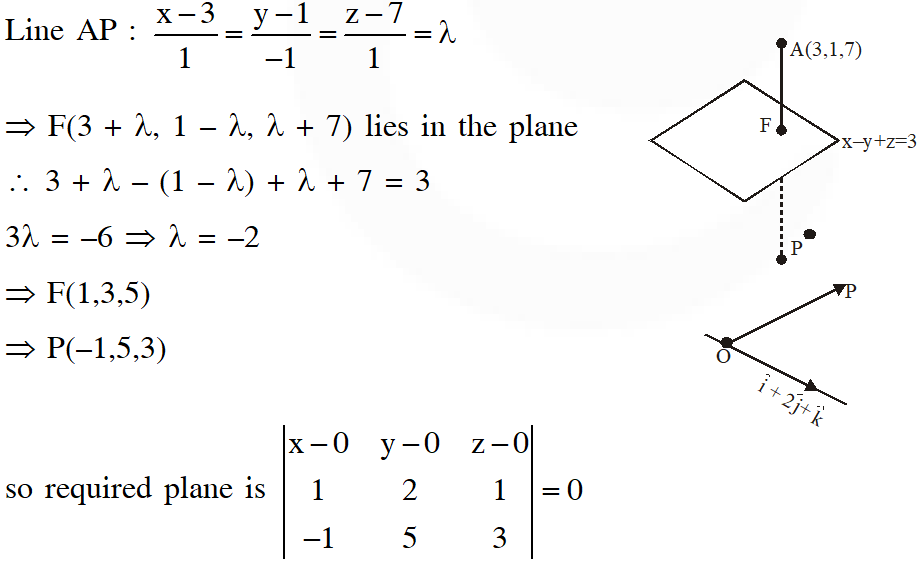$\therefore x-4 y+7 z=0$
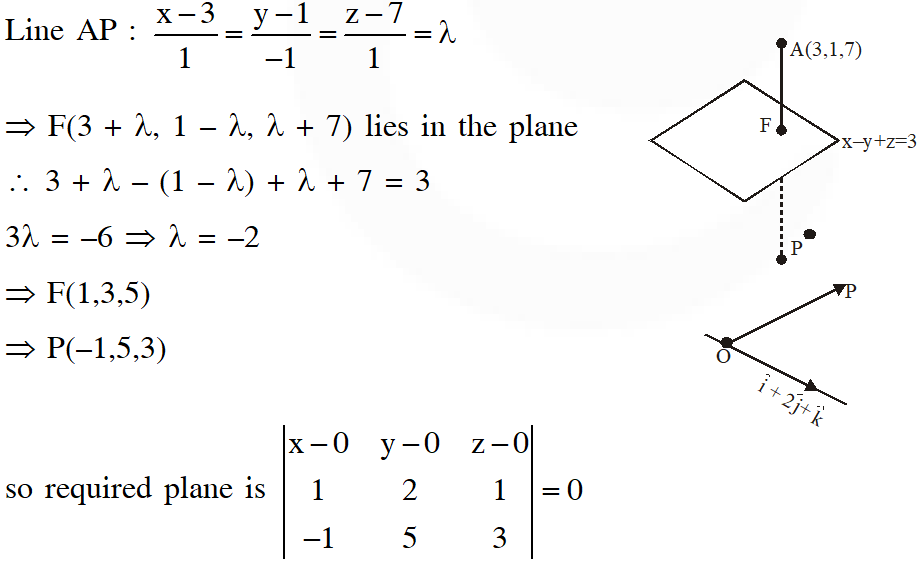$\therefore x-4 y+7 z=0$
Q. The equation of the plane passing through the point (1,1,1) and perpendicular to the planes 2x + y – 2z = 5 and 3x – 6y – 2z = 7, is-
(A) 14x + 2y + 15z = 31
(B) 14x + 2y – 15z = 1
(C) –14x + 2y + 15z = 3
(D) 14x – 2y + 15z = 27
[JEE(Advanced) 2017]
Ans. (A)
Q. Let $P_{1}: 2 x+y-z=3$ and $P_{2}: x+2 y+z=2$ be two planes. Then, which of the following statement(s) is (are) TRUE ?
(A) The line of intersection of $\mathrm{P}_{1}$ and $\mathrm{P}_{2}$ has direction ratios $1,2,-1$
(B) The line $\frac{3 x-4}{9}=\frac{1-3 y}{9}=\frac{z}{3}$ is perpendicular to the line of intersection of $P_{1}$ and $P_{2}$
(C) The acute angle between $\mathrm{P}_{1}$ and $\mathrm{P}_{2}$ is $60^{\circ}$
(D) If $P_{3}$ is the plane passing through the point $(4,2,-2)$ and perpendicular to the line of intersection of $\mathrm{P}_{1}$ and $\mathrm{P}_{2},$ then the distance of the point $(2,1,1)$ from the plane $\mathrm{P}_{2}$ is $\frac{2}{\sqrt{3}}$
[JEE(Advanced) 2018]
Ans. (C,D)
D.C. of line of intersection $(a, b, c)$
$\begin{aligned} \Rightarrow \quad & 2 \mathrm{a}+\mathrm{b}-\mathrm{c}=0 \\ & \mathrm{a}+2 \mathrm{b}+\mathrm{c}=0 \end{aligned}$
$\frac{a}{1+2}=\frac{b}{-1-2}=\frac{c}{4-1}$
$\therefore \quad \mathrm{D} . \mathrm{C} .$ is $(1,-1,1)$
B) $\frac{3 x-4}{9}=\frac{1-3 y}{9}=\frac{z}{3}$
$\Rightarrow \quad \frac{x-4 / 3}{3}=\frac{y-1 / 3}{-3}=\frac{z}{3}$
$\Rightarrow \quad$ lines are parallel.
(C) Acute angle between $\mathrm{P}_{1}$ and $\mathrm{P}_{2}=\cos ^{-1}\left(\frac{2 \times 1+1 \times 2-1 \times 1}{\sqrt{6} \sqrt{6}}\right)$ \[ =\cos ^{-1}\left(\frac{3}{6}\right)=\cos ^{-1}\left(\frac{1}{2}\right)=60^{\circ} \]
(D) Plane is given by $(x-4)-(y-2)+(z+2)=0$ \[ \Rightarrow \quad x-y+z=0 \]
Distance of $(2,1,1)$ from plane $=\frac{2-1+1}{\sqrt{3}}=\frac{2}{\sqrt{3}}$
Q. Consider the cube in the first octant with sides $\mathrm{OP}, \mathrm{OQ}$ and $\mathrm{OR}$ of length $1,$ along the x-axis,
y-axis and z-axis, respectively, where $\mathrm{O}(0,0,0)$ is the origin. Let $\mathrm{S}\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}\right)$ be the centre
of the cube and $T$ be the vertex of the cube opposite to the origin $O$ such that $S$ lies on the diagonal OT.If $\overrightarrow{\mathrm{p}}=\overrightarrow{\mathrm{SP}}, \overrightarrow{\mathrm{q}}=\overrightarrow{\mathrm{SQ}}, \overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{SR}}$ and $\overrightarrow{\mathrm{t}}=\overrightarrow{\mathrm{ST}},$ then the value of $|(\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{q}}) \times(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{t}})|$ is
[JEE(Advanced) 2018]
Ans. 8
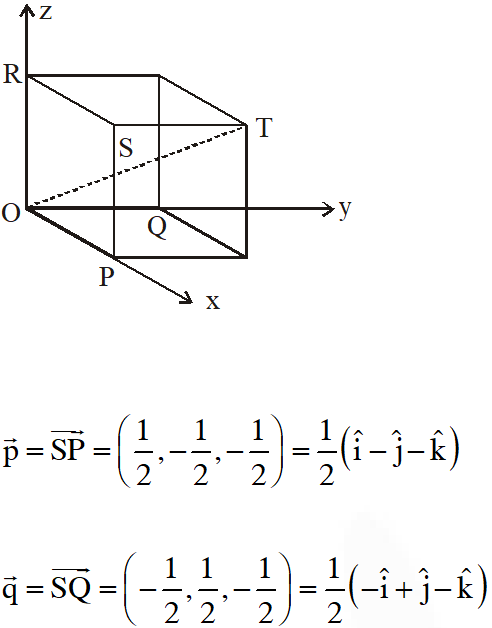
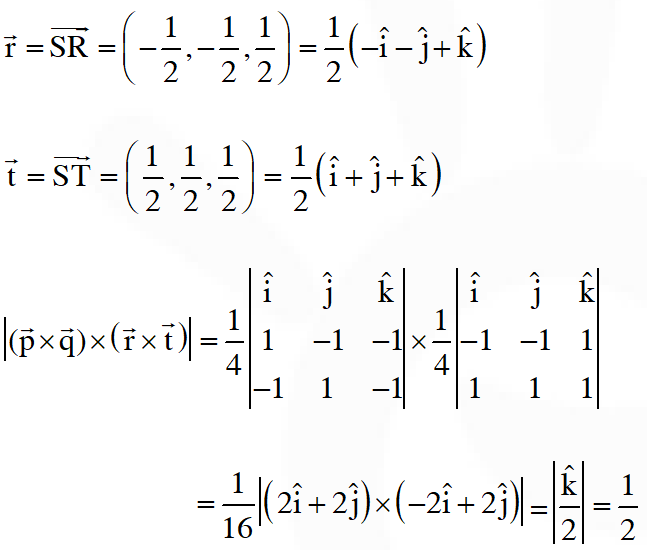
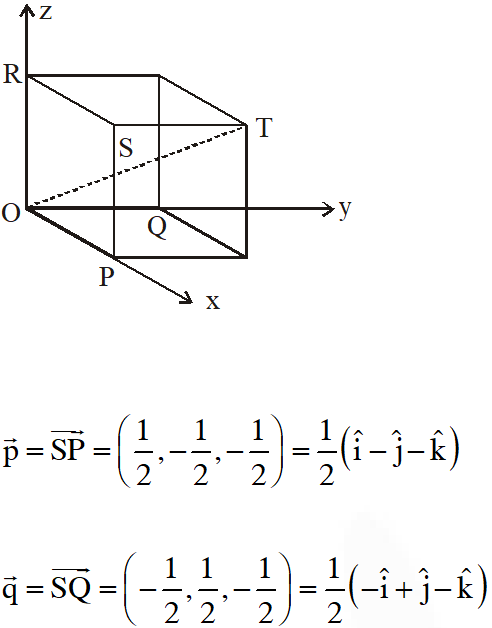
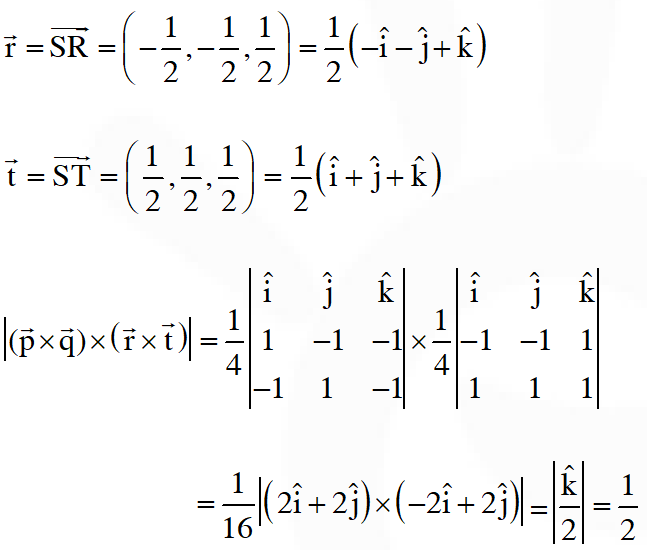
Q. Let P be a point in the first octant, whose image Q in the plane x + y = 3 (that is, the line segment PQ is perpendicular to the plane x + y = 3 and the mid-point of PQ lies in the plane x + y = 3) lies on the z-axis. Let the distance of P from the x-axis be 5. If R is the image of P in the xy-plane, then the length of PR is
Ans. 8
