JEE Main Previous Year Question of Math with Solutions are available at eSaral. Practicing JEE Main Previous Year Papers Questions of mathematics will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. Let the line $\frac{x-2}{3}=\frac{y-1}{-5}=\frac{z+2}{2}$ lie in the plane $x+3 y-\alpha z+\beta=0 .$ Then $(\alpha, \beta)$ equals
(1) (5, – 15) (2) (–5, 5) (3) (6, –17) (4) (–6, 7)
[AIEEE-2009]
Ans. (4)
Line $\frac{x-2}{3}=\frac{y-1}{-5}=\frac{z+2}{2} \ldots .(1)$
Plane $\mathrm{x}+3 \mathrm{y}-\alpha \mathrm{z}+\beta=0 \quad \ldots .(2)$
Point $(2,1,-2)$ put in ( 2)
$2+3+2 \alpha+\beta=0 \Rightarrow 2 \alpha+\beta=-5$
$\mathrm{Now} \mathrm{a}_{1} \mathrm{a}_{2}+\mathrm{b}_{1} \mathrm{b}_{2}+\mathrm{c}_{1} \mathrm{c}_{2}=0$
$3-15-2 \alpha=0 \Rightarrow-12-2 \alpha=0 \Rightarrow \alpha=-6$
$-12+\beta=-5 \Rightarrow \beta=7$
$\therefore \alpha=-6, \beta=7$
Q. The projections of a vector on the three coordinate axis are 6, –3, 2 respectively. The direction cosines of the vector are :-
(1) $\frac{6}{7}, \frac{-3}{7}, \frac{2}{7}$
(2) $\frac{-6}{7}, \frac{-3}{7}, \frac{2}{7}$
(3) 6, –3, 2
(4) $\frac{6}{5}, \frac{-3}{5}, \frac{2}{5}$
[AIEEE-2009]
Ans. (1)
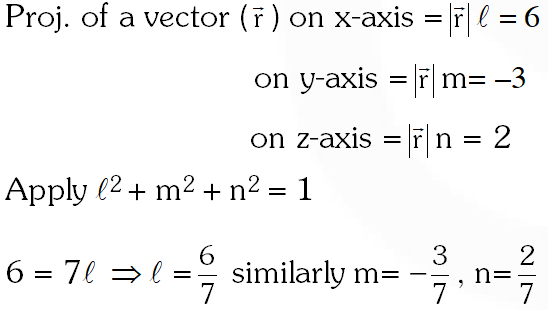
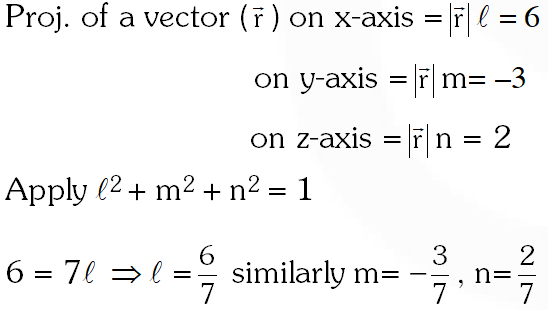
Q. Statement–1 : The point A(3,1,6) is the mirror image of the point B(1, 3, 4) in the plane
x – y + z = 5.
Statement–2 : The plane x – y + z = 5 bisects the line segment joining A(3, 1, 6) and B(1, 3, 4).
(1) Statement–1 is true, Statement–2 is true; Statement–2 is a correct explanation for Statement– 1.
(2) Statement–1 is true, Statement–2 is true ; Statement–2 is not a correct explanation for statement– 1.
(3) Statement–1 is true,n Statement–2 is false.
(4) Statement–1 is false, Statement–2 is true.
[AIEEE-2010]
Ans. (2)
Mirror image of $\mathrm{B}(1,3,4)$ in plane $\mathrm{x}-\mathrm{y}+\mathrm{z}=5$
$\frac{x-1}{1}=\frac{y-3}{-1}=\frac{z-4}{1}=-2 \frac{(1-3+4-5)}{1+1+1}=2$
$\Rightarrow x=3, y=1, z=6$
$\therefore$ mirror image of $\mathrm{B}(1,3,4)$
is $\mathrm{A}(3,1,6)$
statement-1 is correct
statement-2 is true but it is not the correct explanation.
because it is not neccessary that to bisect the line joining (1,3,4) and (3,1,6) plane is always perpendicular to line AB
Q. If the angle between the line $x=\frac{y-1}{2}=\frac{z-3}{\lambda}$ and the plane $x+2 y+3 z=4$ is $\cos ^{-1}(\sqrt{\frac{5}{14}})$, then $\lambda$ equals:-
( 1)$\frac{2}{5}$
( 2)$\frac{5}{3}$
( 3)$\frac{2}{3}$
( 4)$\frac{3}{2}$
[AIEEE-2011]
Ans. (3)
$\frac{x}{1}=\frac{y-1}{2}=\frac{z-3}{\lambda}$ equation of line
equation of plane $x+2 y+3 z=4$
$\sin \theta=\frac{1+4+3 \lambda}{\sqrt{14} \sqrt{1+4}+\lambda^{2}}$
$\Rightarrow \lambda=\frac{2}{3}$
Q. Statement-1: The point $\mathrm{A}(1,0,7)$ is the mirror image of the point $\mathrm{B}(1,6,3)$ in the line:
\[ \frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3} \]
Statement-2: The line : $\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}$ bisects the line segment joining $A(1,0,7)$ and B(1, 6, 3).
(1) Statement-1 is true, Statement-2 is false.
(2) Statement-1 is false, Statement-2 is true
(3) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1
(4) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
[AIEEE-2011]
Ans. (4)
$1(1-1)+2(0-6)+3(7-3)$
$=0-12+12=0$
mid point $\mathrm{AB}(1,3,5)$
lies on $\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}$
Q. The distance of the point (1, –5, 9) from the plane x – y + z = 5 measured along a straight line x = y = z is :
(1) $3 \sqrt{5}$
(2) $10 \sqrt{3}$
(3) $5 \sqrt{3}$
(4) $3 \sqrt{10}$
[AIEEE-2011]
Ans. (2)
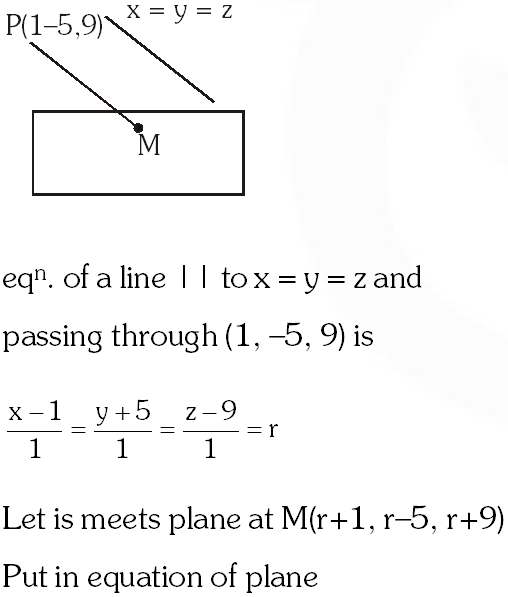
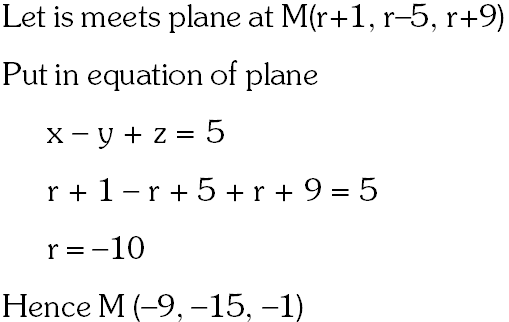Distance $\mathrm{PM}=\sqrt{100+100+100}=10 \sqrt{3}$
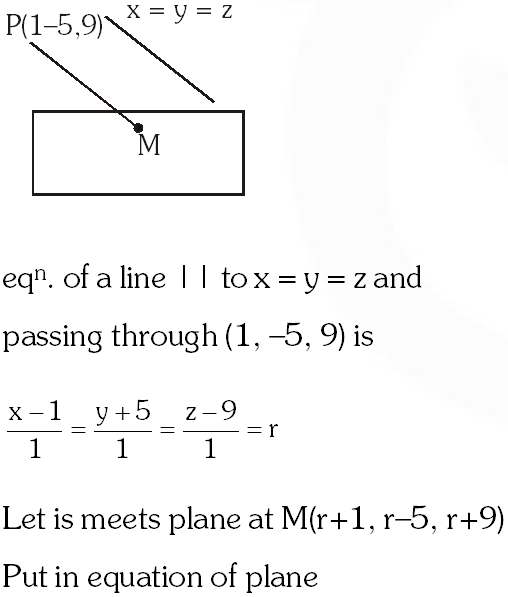
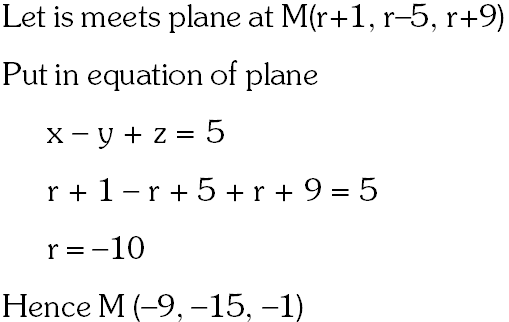Distance $\mathrm{PM}=\sqrt{100+100+100}=10 \sqrt{3}$
Q. An equation of a plane parallel to the plane x – 2y + 2z – 5 = 0 and at a unit distance from the origin is :
(1) x – 2y + 2z + 5 = 0
(2) x – 2y + 2z – 3 = 0
(3) x – 2y + 2z + 1 = 0
(4) x – 2y + 2z – 1 = 0
[AIEEE-2012]
Ans. (2)
Equation of plane parallel to
$x-2 y+2 z-5=0$
is $x-2 y+2 z=k$
Distance of plane from origen $=1$
$\left|\frac{k}{\sqrt{9}}\right|=1$
$\mathrm{k}=\pm 3$
Equation of required plane is
$x-2 y+2 z \pm 3=0$
Q. If the lines $\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}$ and $\frac{x-3}{1}=\frac{y-k}{2}=\frac{z}{1}$ intersect, then $k$ is equal to :
(1) 0
(2) – 1
( 3)$\frac{2}{9}$
( 4)$\frac{9}{2}$
[AIEEE-2012]
Ans. (4)
$\left|\begin{array}{ccc}{3-1} & {\mathrm{K}+1} & {0-1} \\ {2} & {3} & {4} \\ {1} & {2} & {1}\end{array}\right|=0 \Rightarrow\left|\begin{array}{ccc}{2} & {\mathrm{K}+1} & {-1} \\ {2} & {3} & {4} \\ {1} & {2} & {1}\end{array}\right|=0$
$\Rightarrow 2 \mathrm{K}-9=0 \Rightarrow \mathrm{K}=\frac{9}{2}$
Q. Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is :-
( 1)$\frac{3}{2}$
( 2)$\frac{5}{2}$
(3) $\frac{7}{2}$
( 4)$\frac{9}{2}$
[JEE-MAIN 2013]
Ans. (3)
$4 x+2 y+4 z+5=0$
$4 x+2 y+4 z-16=0$
$\Rightarrow \quad d=\left|\frac{21}{\sqrt{36}}\right|=\frac{7}{2}$
Q. If the lines $\frac{x-2}{1}=\frac{y-3}{1}=\frac{z-4}{-k}$ and $\frac{x-1}{k}=\frac{y-4}{2}=\frac{z-5}{1}$ are coplanar, then $k$ can have :
(1) any value
(2) exactly one value
(3) exactly two values
(4) exactly three values.
[JEE-MAIN 2013]
Ans. (3)
$\Rightarrow(\bar{a}-\bar{b}) \cdot(\bar{c} \times \bar{d})=0$
$\Rightarrow\left|\begin{array}{ccc}{1} & {-1} & {-1} \\ {1} & {1} & {-k} \\ {k} & {2} & {1}\end{array}\right|=0$
$\Rightarrow \quad(1+2 k)+\left(1+k^{2}\right)-(2-k)=0$
$\Rightarrow \quad \mathrm{k}^{2}+3 \mathrm{k}=0<\begin{array}{c}{0} \\ {-3}\end{array}$
Q. A vector $\overrightarrow{\mathrm{n}}$ is inclined to x-axis at $45^{\circ},$ to $\mathrm{y}$ -axis at $60^{\circ}$ and at an acute angle to z-axis. If $\overrightarrow{\mathrm{n}}$ is a normal to a plane passing through the point $(\sqrt{2},-1,1),$ then the equation of the plane is :
(1) $\sqrt{2} x-y-z=2$
(2) $\sqrt{2} x+y+z=2$
(3) $3 \sqrt{2} x-4 y-3 z=7$
(4) $4 \sqrt{2} x+7 y+z=2$
[JEE-MAIN Online 2013]
Ans. (2)
Let $\alpha, \beta, \gamma$ v be direction cosine of vector $\vec{n}$
$\alpha^{2}+\beta^{2}+\gamma^{2}=1$
$\frac{1}{2}+\frac{1}{4}+\gamma^{2}=1$
$\gamma=\frac{1}{2} \quad\left\{-\frac{1}{2} \text { rejected }\right\}$
$\overline{\mathrm{n}}=\frac{\hat{\mathrm{i}}}{\sqrt{2}}+\frac{\hat{\mathrm{j}}}{2}+\frac{\hat{\mathrm{k}}}{2}=\sqrt{2 \hat{\mathrm{i}}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}$
$\overline{\mathrm{a}}=\sqrt{2} \hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}$
$d=\bar{a} \cdot \bar{n}=2-1+1=2$
$\overline{\mathrm{r}} \cdot(\sqrt{2} \hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})=2$
$\sqrt{2} x+y+z=2$
Q. The acute angle between two lines such that the direction cosines $\ell, \mathrm{m}, \mathrm{n}$ of each of them satisfy the equations $\ell+\mathrm{m}+\mathrm{n}=0$ and $\ell^{2}+\mathrm{m}^{2}-\mathrm{n}^{2}=0$ is :-
(1) $30^{\circ}$ (2) $45^{\circ}$ (3) $60^{\circ}$ (4) $15^{\circ}$
[JEE-MAIN Online 2013]
Ans. (3)
$\begin{array}{rl}{1+\mathrm{m}+\mathrm{n}} & {=0 ; \ell^{2}+\mathrm{m}^{2}-\mathrm{n}^{2}=0} \\ {\mathrm{a} \ell=-(\mathrm{m}+\mathrm{n})} & {} \\ {(\mathrm{m}+\mathrm{n})^{2}+\mathrm{m}^{2}-\mathrm{n}^{2}} & {=0} \\ {(\mathrm{m}+\mathrm{n})[\mathrm{m}+\mathrm{n}+\mathrm{m}-\mathrm{n}]} & {=0} \\ {\mathrm{m}+\mathrm{n}=0} & {\mathrm{m}=0} \\ {\mathrm{m}=-\mathrm{n}}\end{array}$
Dr's of line $1 \Rightarrow 0,-\mathrm{n}, \mathrm{n}$ or $0,-1,1$
Dr's of line $2 \Rightarrow-\mathrm{n}, 0, \mathrm{n}$ or $-1,0,1$
$\cos \theta=\frac{1}{\sqrt{2} \sqrt{2}}$
$\theta=60^{\circ}$
Q. Let Q be the foot of perpendicular from the origin to the plane 4x – 3y + z + 13 = 0 and R be a point (–1, 1, –6) on the plane. Then length QR is :
(1) $3 \sqrt{\frac{7}{2}}$
(2) $\sqrt{14}$
(3) $\sqrt{\frac{19}{2}}$
(4) $\frac{3}{\sqrt{2}}$
[JEE-MAIN Online 2013]
Ans. (1)
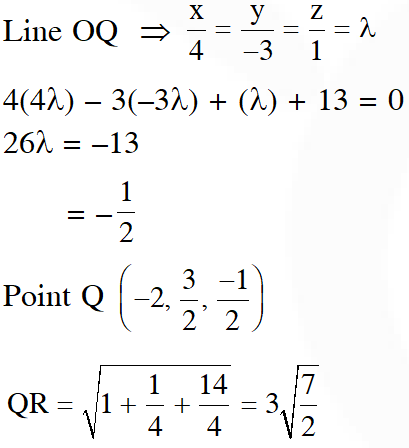
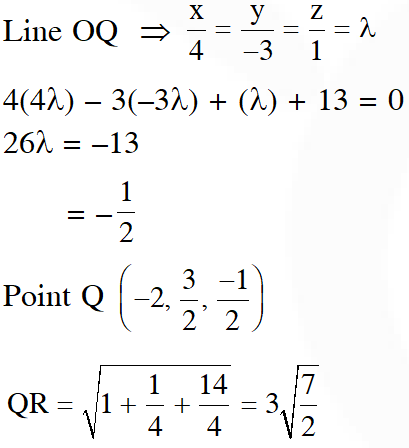
Q. If the projections of a line segment on thex, y and z-axes in 3-dimensional space are 2, 3 and 6 respectively, then the length ofthe line segment is :
(1) 7 (2) 9 (3) 12 (4) 6
[JEE-MAIN Online 2013]
Ans. (1)
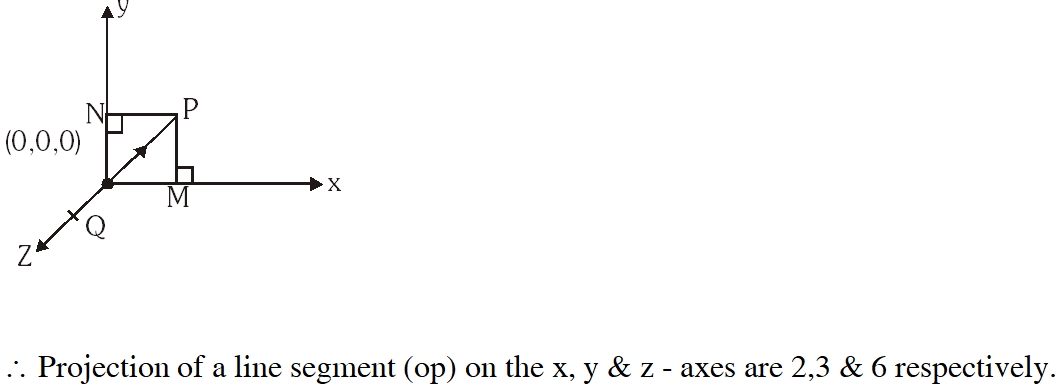i.e. $[\mathrm{OM}=2, \mathrm{ON}=3, \mathrm{OQ}=6]$
$\therefore \mathrm{P}(2,3,6)$
$\begin{aligned} \therefore \mathrm{OP} &=\sqrt{2^{2}+3^{2}+6^{2}} \\ &=\sqrt{49}=7 \end{aligned}$
i.e. $[\mathrm{OM}=2, \mathrm{ON}=3, \mathrm{OQ}=6]$
$\therefore \mathrm{P}(2,3,6)$
$\begin{aligned} \therefore \mathrm{OP} &=\sqrt{2^{2}+3^{2}+6^{2}} \\ &=\sqrt{49}=7 \end{aligned}$
Q. If two lines $L_{1}$ and $L_{2}$ in space, are defined by $\mathrm{L}_{1}=\{\mathrm{x}=\sqrt{\lambda} \mathrm{y}+(\sqrt{\lambda}-1)$
$\mathrm{z}=(\sqrt{\lambda}-1) \mathrm{y}+\sqrt{\lambda}\}$ and
$\mathrm{L}_{2}=\{\mathrm{x}=\sqrt{\mu} \mathrm{y}+(1-\sqrt{\mu})$
$\mathrm{z}=(1-\sqrt{\mu}) \mathrm{y}+\sqrt{\mu}\}$
then $\mathrm{L}_{1}$ is perpendicular to $\mathrm{L}_{2},$ for all non-negative reals $\lambda$ and $\mu,$ such that :
(1) $\lambda=\mu$
(2) $\lambda \neq \mu$
(3) $\sqrt{\lambda}+\sqrt{\mu}=1$
(4) $\lambda+\mu=0$
[JEE-MAIN Online 2013]
Ans. (1,4)
$\mathrm{L}_{1}=\{\mathrm{x}=\sqrt{\lambda} \mathrm{y}+(\sqrt{\lambda}-1), \mathrm{z}=(\sqrt{\lambda}-1) \mathrm{y}+\sqrt{\lambda}\}$
$\therefore \mathrm{L}_{1}: \frac{\mathrm{x}-(\sqrt{\lambda}-1)}{\sqrt{\lambda}}=\frac{\mathrm{y}-0}{1}=\frac{\mathrm{Z}-\sqrt{\lambda}}{(\sqrt{\lambda}-1)} \quad \& \mathrm{L}_{2}:\{\mathrm{x}=\sqrt{\mu} \mathrm{y}+(1-\sqrt{\mu}), \mathrm{z}=(1-\sqrt{\mu}) \mathrm{y}+\sqrt{\mu}\}$
$\therefore \mathrm{L}_{2}: \frac{\mathrm{x}-(1-\sqrt{\mu})}{\sqrt{\mu}}=\frac{\mathrm{y}-0}{1}=\frac{\mathrm{z}-\sqrt{\mu}}{(1-\sqrt{\mu})}$
$\therefore \mathrm{L}_{1} \perp^{r} \mathrm{L}_{2} \Rightarrow(\sqrt{\lambda})(\sqrt{\mu})+1+(\sqrt{\lambda}-1)(1-\sqrt{\mu})=0$
$\Rightarrow \sqrt{\lambda} \sqrt{\mu}+1-\sqrt{\lambda} \sqrt{\mu}+\sqrt{\lambda}+\sqrt{\mu}-1=0$
$\Rightarrow \sqrt{\lambda}+\sqrt{\mu}=0 \Rightarrow \lambda=\mu=0$
Q. The equation of a plane through the line of intersection of the planes x + 2y = 3, y – 2z+ 1 = 0, and perpendicular to the first plane is :
(1) 2x – y + 7z = 11
(2) 2x – y + 10 z = 11
(3) 2x – y – 9z = 10
(4) 2x – y – 10z = 9
[JEE-MAIN Online 2013]
Ans. (2)
$(x+2 y-3)+\lambda(y-2 z+1)=0$
$(1)(1)+(2+\lambda) 2+(-2 \lambda) \times 0=0$
$1+4+2 \lambda=0$
$\lambda=-\frac{5}{2}$
$(x+2 y-3)-\frac{5}{2}(y-2 z+1)=0$
$2 \mathrm{x}-\mathrm{y}+10 \mathrm{z}-11=0$
Q. Let ABC be a triangle with vertices at points $\mathrm{A}(2,3,5), \mathrm{B}(-1,3,2)$ and $\mathrm{C}(\lambda, 5, \mu)$ in three dimensional space. If the median through A is equally inclined with the axes, then $(\lambda, \mu$.) is equal to :
(1) (10, 7) (2) (7.5) (3) (7, 10) (4) (5,7)
[JEE-MAIN Online 2013]
Ans. (3)
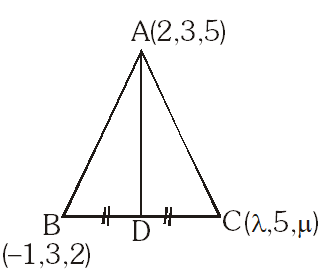
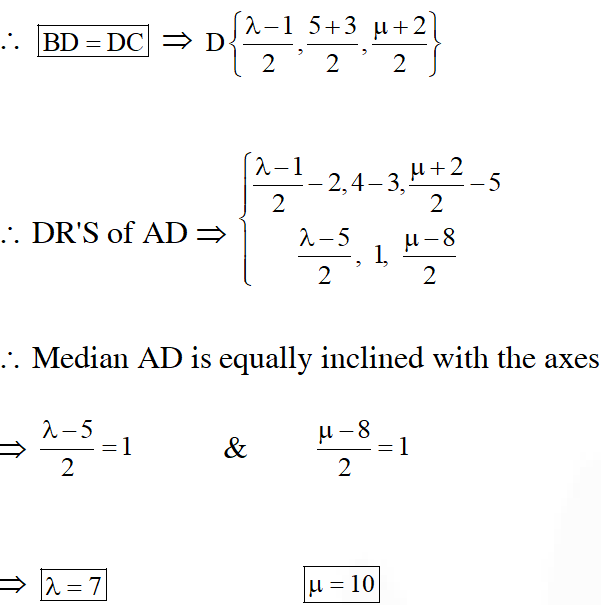
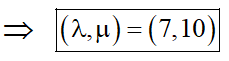
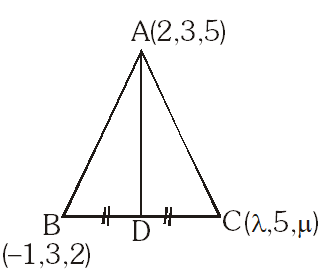
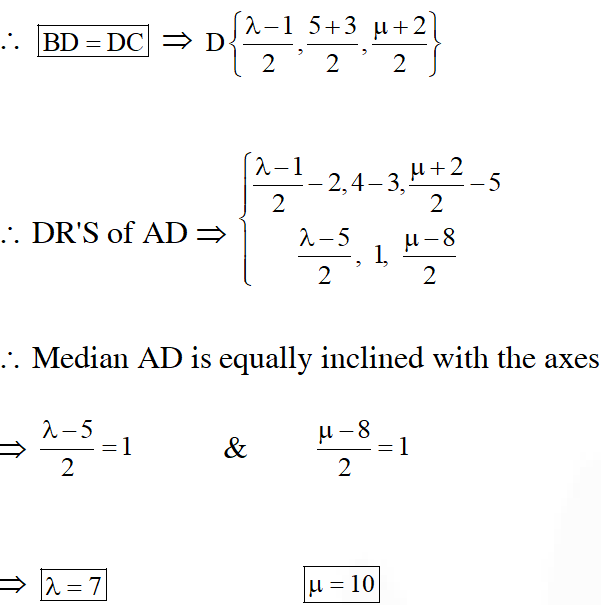
Q. The angle between the lines whose direction cosines satisfy the equations $\ell+\mathrm{m}+\mathrm{n}=0$ and $\ell^{2}=\mathrm{m}^{2}+\mathrm{n}^{2}$ is
( 1)$\frac{\pi}{3}$
( 2)$\frac{\pi}{4}$
( 3)$\frac{\pi}{6}$
(4) $\frac{\pi}{2}$
[JEE-MAIN 2014]
Ans. (1)
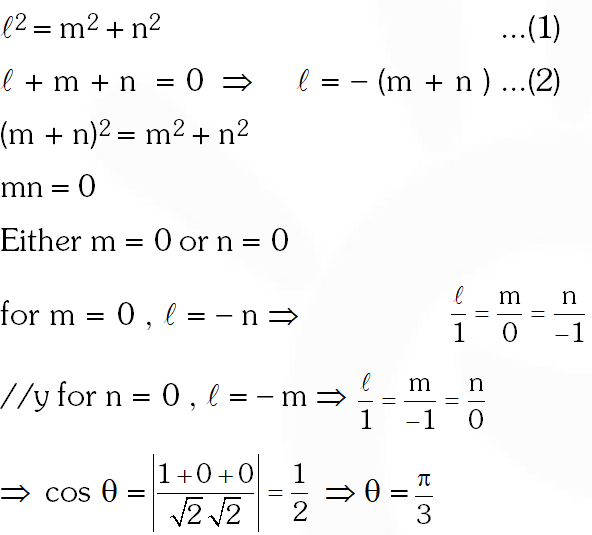
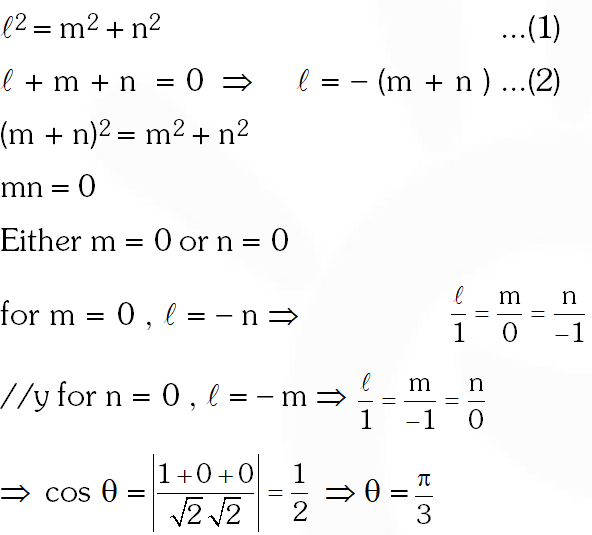
Q. The image of the line $\frac{x-1}{3}=\frac{y-3}{1}=\frac{z-4}{-5}$ in the plane $2 x-y+z+3=0$ is the line:
(1) $\frac{x+3}{3}=\frac{y-5}{1}=\frac{z-2}{-5}$
(2) $\frac{x+3}{-3}=\frac{y-5}{-1}=\frac{z+2}{5}$
(3) $\frac{x-3}{3}=\frac{y+5}{1}=\frac{z-2}{-5}$
(4) $\frac{x-3}{-3}=\frac{y+5}{-1}=\frac{z-2}{5}$
[JEE-MAIN 2014]
Ans. (1)
$\mathrm{L}: \frac{\mathrm{x}-1}{3}=\frac{\mathrm{y}-3}{1}=\frac{\mathrm{z}-4}{-5}$
$P: 2 x-y+z+3=0$
It can be observed given line is parallel to given plane.
Image of $(1,3,4)$ in given plane can be calculated as
$\frac{x-1}{2}=\frac{y-3}{-1}=\frac{z-4}{1}=\frac{-2(2 \times 1-3+4+3)}{6}=-2$
$\Rightarrow x=-3 ; y=5 ; z=2$
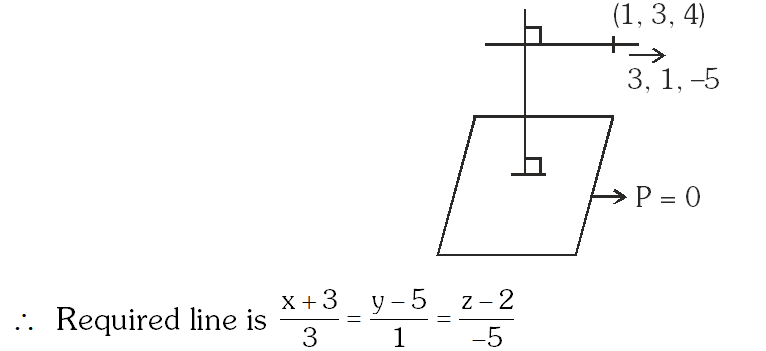
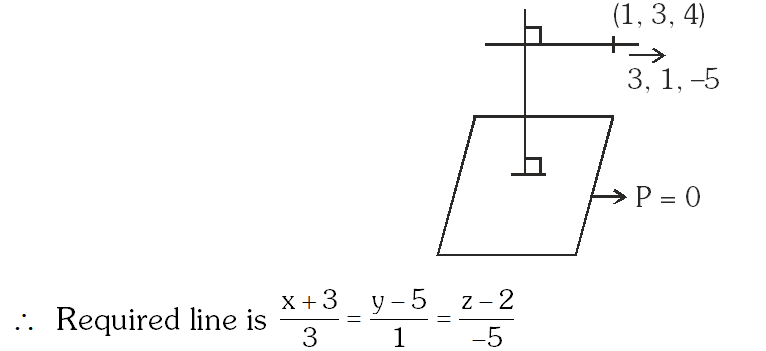
Q. The equation of the plane containing the line 2x – 5y + z = 3 ; x + y + 4z = 5, and parallel to the plane, x + 3y + 6z = 1, is :
(1)x + 3y + 6z = 7
(2) 2x + 6y + 12z = – 13
(3) 2x + 6y + 12z = 13
(4) x + 3y + 6z = – 7
[JEE(Main)-2015]
Ans. (1)
Let equation of plane parallel to $\mathrm{x}+3 \mathrm{y}+6 \mathrm{z}=1$ is $\mathrm{x}+3 \mathrm{y}+6 \mathrm{z}=\lambda$ point on line of intersection is $(4,1,0),$ it also lie on plane $x+3 y+6 z=\lambda$ so required plane is $x+3 y+6 z=7$
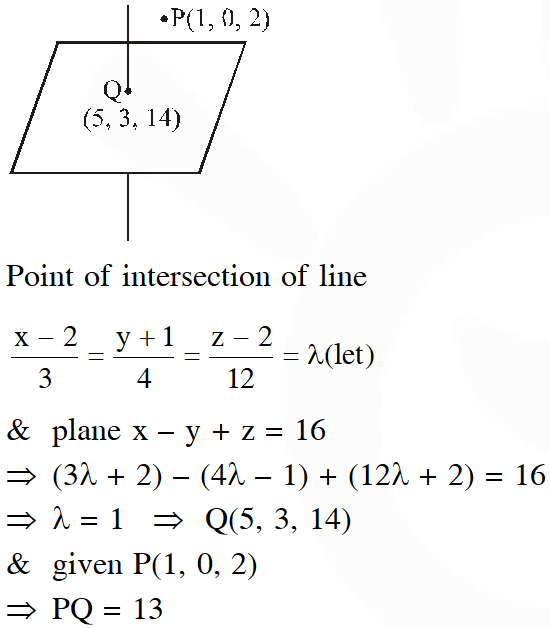
Q. The distance of the point (1, 0, 2) from the point of intersection of the line $\frac{\mathrm{x}-2}{3}=\frac{\mathrm{y}+1}{4}=\frac{\mathrm{z}-2}{12}$ and the plane $\mathrm{x}-\mathrm{y}+\mathrm{z}=16,$ is :
(1) $3 \sqrt{21}$
(2) 13
(3) $2 \sqrt{14}$
(4) 8
[JEE(Main)-2015]
Ans. (2)
Q. The distance of the point (1, –5, 9) from the plane x – y + z = 5 measured along the line x = y = z is :
(1) $\frac{20}{3}$
(2) $3 \sqrt{10}$
(3) $10 \sqrt{3}$
( 4)$\frac{10}{\sqrt{3}}$
[JEE(Main)-2016]
Ans. (3)
Equation of line parallel to $\mathrm{x}=\mathrm{y}=\mathrm{z}$ through $(1,-5,9)$ is $\frac{\mathrm{x}-1}{1}=\frac{\mathrm{y}+5}{1}=\frac{\mathrm{z}-9}{1}=\lambda$
If $\mathrm{P}(\lambda+1, \lambda-5, \lambda+9)$ be point of intesection of line and plane.
$\Rightarrow$ Required distance $=10 \sqrt{3}$
$\Rightarrow$ Required distance $=10 \sqrt{3}$
Q. If the line, $\frac{x-3}{2}=\frac{y+2}{-1}=\frac{z+4}{3}$ lies in the plane, $1 x+m y-z=9,$ then $1^{2}+m^{2}$ is equal to :-
(1) 2 (2) 26 (3) 18 (4) 5
[JEE(Main)-2016]
Ans. (1)
Given line
\[ \frac{x-3}{2}=\frac{y+2}{-1}=\frac{z+4}{3} \]
and Given plane is $\ell \mathrm{x}+\mathrm{my}-\mathrm{z}=9$
Now, it is given that line lies on plane $\therefore 2 \ell-\mathrm{m}-3=0 \Rightarrow 2 \ell-\mathrm{m}=3$
Also, $(3,-2,-4)$ lies on plane
\[ 3 \ell-2 m=5 \]
Solving ( 1) and $(2),$ we get
\[ \ell=1, \mathrm{m}=-1 \]
$\therefore \ell^{2}+\mathrm{m}^{2}=2$
Q. If the image of the point P(1, –2, 3) in the plane, 2x + 3y – 4z + 22 = 0 measured parallel to line, $\frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{4}=\frac{\mathrm{z}}{5}$ is $\mathrm{Q},$ then $\mathrm{PQ}$ is equal to :-
(1) $6 \sqrt{5}$
(2) $3 \sqrt{5}$
(3) $2 \sqrt{42}$
(4) $\sqrt{42}$
[JEE(Main)-2017]
Ans. (3)
Line $\mathrm{PQ} ; \frac{\mathrm{x}-1}{1}=\frac{\mathrm{y}+2}{4}=\frac{\mathrm{z}-3}{5}$
Let $\mathrm{F}(\lambda+1,4 \lambda-2,5 \lambda+3)$
F lies on the plane
$2(\lambda+1)+3(4 \lambda-2)-4(5 \lambda+3)+22=0$
$\Rightarrow-6 \lambda+6=0 \Rightarrow \lambda=1$
$\mathrm{F}(2,2,8)$
$\mathrm{PQ}=2 \quad \mathrm{PF}=2 \sqrt{42}$
F lies on the plane
$2(\lambda+1)+3(4 \lambda-2)-4(5 \lambda+3)+22=0$
$\Rightarrow-6 \lambda+6=0 \Rightarrow \lambda=1$
$\mathrm{F}(2,2,8)$
$\mathrm{PQ}=2 \quad \mathrm{PF}=2 \sqrt{42}$
Q. The distantce of the point (1, 3, –7) from the plane passing through the point (1, 1, –1), havingnormal perpendicular to both the lines $\frac{x-1}{1}=\frac{y+2}{-2}=\frac{z-4}{3}$ and $\frac{x-2}{2}=\frac{y+1}{-1}=\frac{z+7}{-1},$ is :
(1) $\frac{10}{\sqrt{74}}$
(2) $\frac{20}{\sqrt{74}}$
(3) $\frac{10}{\sqrt{83}}$
(4) $\frac{5}{\sqrt{83}}$
[JEE(Main)-2017]
Ans. (1)
Normal vector
$\left|\begin{array}{ccc}{\hat{\mathrm{i}}} & {\hat{\mathrm{j}}} & {\hat{\mathrm{k}}} \\ {1} & {-2} & {3} \\ {2} & {-1} & {-1}\end{array}\right|=5 \hat{\mathrm{i}}+7 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$
So plane is 5(x – 1) + 7(y + 1) + 3(z + 1) = 0
$\Rightarrow 5 x+7 y+3 z+5=0$
Distance $\frac{5+21-21+5}{\sqrt{25+49+9}}=\frac{10}{\sqrt{83}}$
Q. The length of the projection of the line segment joining the points (5, –1, 4) and (4, –1, 3) on the plane, x + y + z = 7 is :
( 1)$\frac{2}{3}$
(2) $\frac{1}{3}$
(3) $\sqrt{\frac{2}{3}}$
(4) $\frac{2}{\sqrt{3}}$
[JEE(Main)-2018]
Ans. (3)
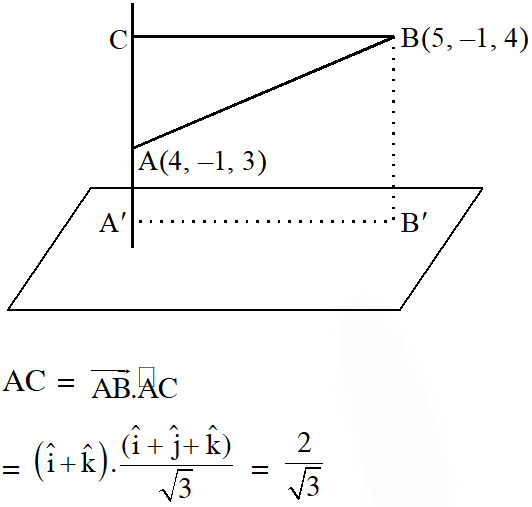
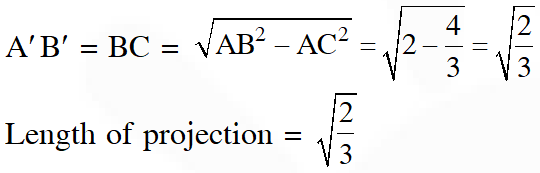
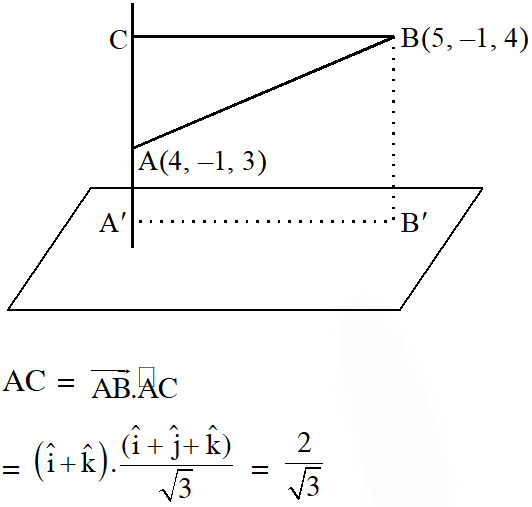
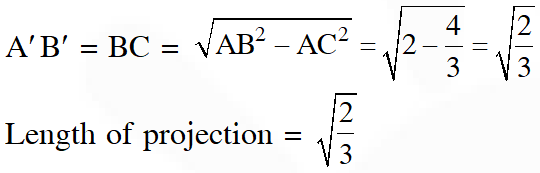
Q. If $\mathrm{L}_{1}$ is the line of intersection of the planes $2 \mathrm{x}-2 \mathrm{y}+3 \mathrm{z}-2=0, \mathrm{x}-\mathrm{y}+\mathrm{z}+1=0$ and $\mathrm{L}_{2}$ is the line of intersection of the planes $\mathrm{x}+2 \mathrm{y}-\mathrm{z}-3=0,3 \mathrm{x}-\mathrm{y}+2 \mathrm{z}-1=0,$ then the distance of the origin from the plane, containing the lines $L_{1}$ and $L_{2}$ is $z$
(1) $\frac{1}{3 \sqrt{2}}$
(2) $\frac{1}{2 \sqrt{2}}$
(3) $\frac{1}{\sqrt{2}}$
( 4)$\frac{1}{4 \sqrt{2}}$
[JEE(Main)-2018]
Ans. (1)
Plane passes through line of intersectuion of first two planes is $(2 x-2 y+3 z-2)+\lambda(x-y+z+1)=0$
$\mathrm{x}(\lambda+2)-\mathrm{y}(2+\lambda)+\mathrm{z}(\lambda+3)+(\lambda-2)=0 \ldots \ldots(1)$
is having infinite number of solution with x + 2y – z – 3 = 0 and 3x – y + 2z – 1 = 0 then
$\left|\begin{array}{ccc}{(\lambda+2)} & {-(\lambda+2)} & {(\lambda+3)} \\ {1} & {2} & {-1} \\ {3} & {-1} & {2}\end{array}\right|=0$
Solving $\lambda=5$ $7 x-7 y+8 z+3=0$
perpendicular distance from $(0,0,0)$
is $\frac{3}{\sqrt{162}}=\frac{1}{3 \sqrt{2}}$
Comments
Pranuu
June 10, 2021, 4:47 p.m.
Hi,im studying 12th standard i jav attemted 2mains but my result is below 50percentile and now this is june i dont start my preparation what to do now
Reddy
Sept. 2, 2020, 9:26 p.m.
Really very helpful tqqq &update ur app like 2020 Jan shifts & sept shifts