JEE Main Previous Year Question of Physics with Solutions are available here. Practicing JEE Main Previous Year Papers Questions of Physics will help all the JEE aspirants in realizing the question pattern as well as help in analyzing their weak & strong areas.
Get detailed Class 11th &12th Physics Notes to prepare for Boards as well as competitive exams like IIT JEE, NEET etc.
eSaral helps the students in clearing and understanding each topic in a better way. eSaral is providing complete chapter-wise notes of Class 11th and 12th both for all subjects.
Besides this, eSaral also offers NCERT Solutions, Previous year questions for JEE Main and Advance, Practice questions, Test Series for JEE Main, JEE Advanced and NEET, Important questions of Physics, Chemistry, Math, and Biology and many more.
Download eSaral app for free study material and video tutorials.
Q. In a series LCR circuit R = $200 \Omega$ and the voltage and the frequency of the main supply is 220 V and 50 Hz respectively. On taking out the capacitance from the circuit the current lages behind the voltage by $30^{\circ}$. On taking out the inductor from the circuit the current leads the voltage by $30^{\circ}$. The power dissipated in the LCR circuit is :
(1) 242 W
(2) 305 W
(3) 210 W
(4) Zero W
[AIEEE - 2010]
Ans. (1)
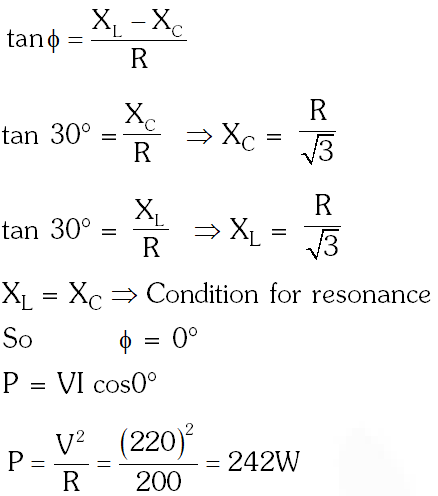
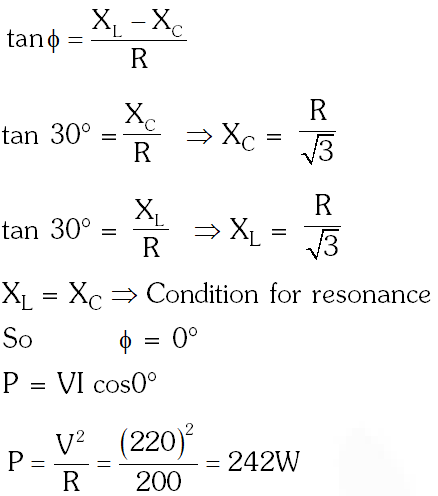
Q. A fully charged capacitor C with intial charge $\mathrm{q}_{0}$ is connected to a coil of self inductance L at t = 0. The time at which the energy is stored equally between the electric and the magnetic fields is :-
(1) $2 \pi \sqrt{\mathrm{LC}}$
(2) $\sqrt{1 C}$
(3) $\pi \sqrt{\mathrm{LC}}$
(4) $\frac{\pi}{4} \sqrt{\mathrm{LC}}$
[AIEEE - 2011]
Ans. (4)
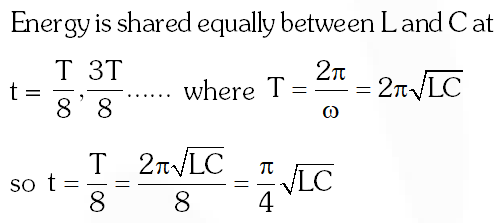
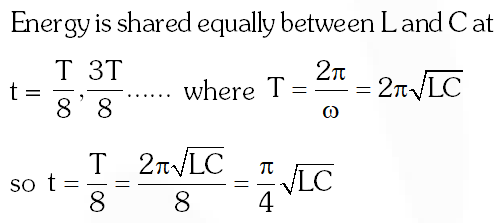
Q. In an LCR circuit as shown below both switches are open initially. Now switch S1 is closed, $\mathrm{S}_{2}$ kept open, (q is charge on the capacitor and $\tau=\mathrm{RC}$ is Capacitive time constant). Which of the following statement is correct?
(1) Work done by the battery is half of the energy dissipated in the resistor
(2) At t $=\tau, q=C \sqrt{/ 2}$
(3) At $\mathrm{t}=2 \pi, \mathrm{q}=\mathrm{CV}\left(1-\mathrm{e}^{-2}\right)$
(4) At $\mathrm{t}=\frac{\tau}{2}, \mathrm{q}=\mathrm{CV}\left(1-\mathrm{e}^{-1}\right)$
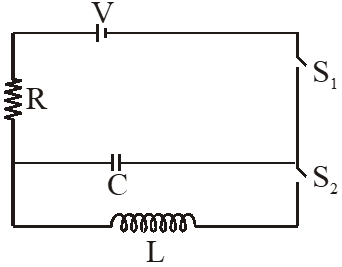[JEE Main-2013]
[JEE Main-2013]
Ans. (3)
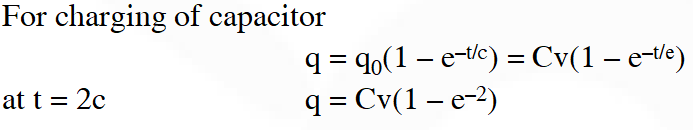
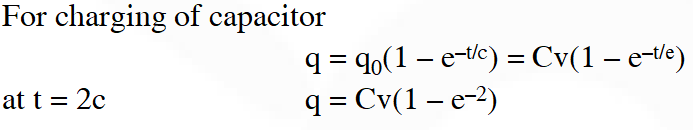
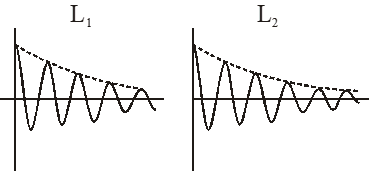
Q. An LCR circuit is equivalent to a damped pendulum. In an LCR circuit the capacitor is charged to $\mathrm{Q}_{0}$ and then connected to the L and R as shown below. If a student plots graphs of the square of maximum charge on the capacitor with time (t) for two different values $\mathrm{L}_{1}$ and $\mathrm{L}_{2}\left(\mathrm{L}_{1}>\mathrm{L}_{2}\right)$ of L then which of the following represents this graph correctly ? (plots are schematic and not drawn to scale)
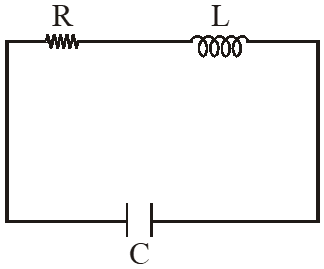
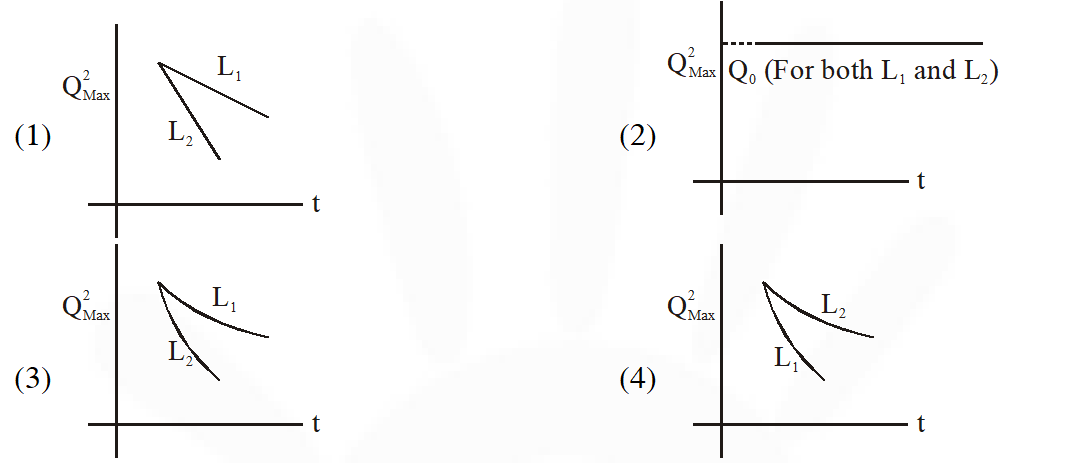[JEE Main-2015]
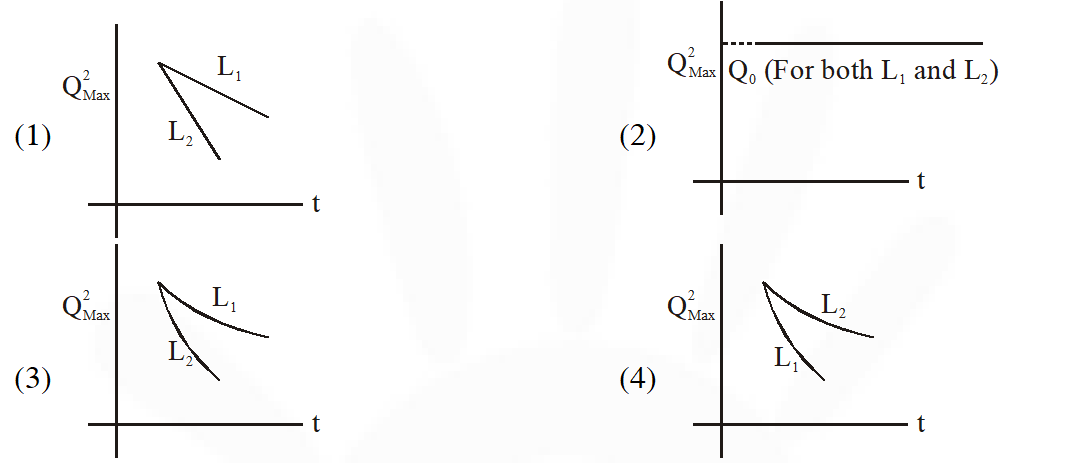[JEE Main-2015]
Ans. (3)
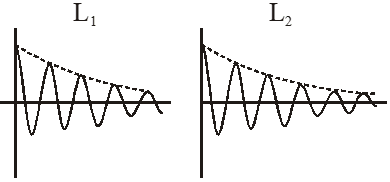
As damping is happening its amplitude would vary as
The oscillations decay exponentially and will be proportional to $\mathrm{e}^{-\gamma t}$ where $\gamma$ depends inversely on L.
So as inductance increases decay becomes slower
for
Q. An arc lamp requires a direct current of 10A at 80V to function. If it is connected to a 220V (rms), 50 Hz AC supply, the series inductor needed for it to work is close to :-
(1) 0.065 H
(2) 80 H
(3) 0.08 H
(4) 0.044 H
[JEE Main-2016]
Ans. (1)
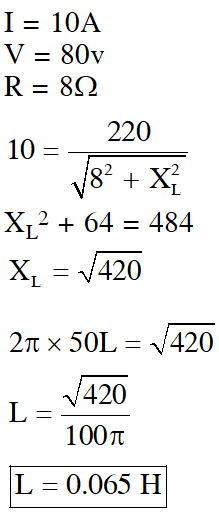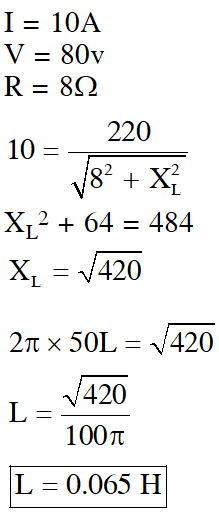As damping is happening its amplitude would vary as
The oscillations decay exponentially and will be proportional to $\mathrm{e}^{-\gamma t}$ where $\gamma$ depends inversely on L.
So as inductance increases decay becomes slower
for
As damping is happening its amplitude would vary as
The oscillations decay exponentially and will be proportional to $\mathrm{e}^{-\gamma t}$ where $\gamma$ depends inversely on L.
So as inductance increases decay becomes slower
for
Q. For an RLC circuit driven with voltage of amplitude $\mathrm{v}_{\mathrm{m}}$ and frequency $\mathrm{w}_{0}=\frac{1}{\sqrt{\mathrm{LC}}}$ the current exhibits resonance. The quality factor, Q is given by :
(1) $\frac{\omega_{0} \mathrm{R}}{\mathrm{L}}$
( 2)$\frac{\mathrm{R}}{\left(\omega_{0} \mathrm{C}\right)}$
(3) $\frac{\mathrm{CR}}{\omega_{0}}$
(4) $\frac{\omega_{0} \mathrm{L}}{\mathrm{R}}$
[JEE Main-2018]
Ans. (4)
Quality factor $=\frac{\omega_{0} \mathrm{L}}{\mathrm{R}}$
Q. In an a. c. circuit, the instantaneous e.m.f. and current are given by e = 100 sin 30 t i = 20
sin $\left(30 t-\frac{\pi}{4}\right)$
In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively.
(1) $\frac{1000}{\sqrt{2}}, 10$
(2) $\frac{50}{\sqrt{2}}, 0$
(3) 50, 0
(4) 50, 10
[JEE Main-2018]
Ans. (1)
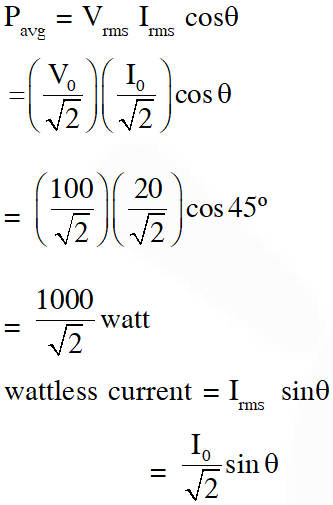
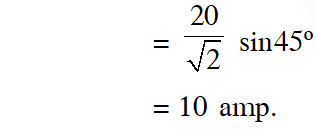
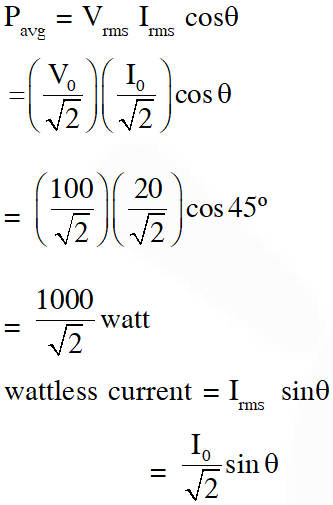
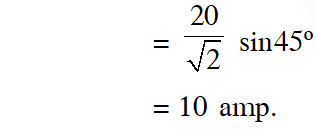
Comments
Zeeshan
Oct. 29, 2020, 1:53 p.m.
Thanks Buddy. Whatever question are there......They are quality based. Easy, Medium, Hard sab h. Thanks mate.
HUGEDICKLIKE fan of Tanmay bhai
Aug. 29, 2020, 7:01 p.m.
Arey bhenchod. Tu bhi previous year questions dekh ke exam dene jayega