JEE Advanced Previous Year Questions of Chemistry with Solutions are available at eSaral. Practicing JEE Advanced Previous Year Papers Questions of Chemistry will help the JEE aspirants in realizing the question pattern as well as help in analyzing weak & strong areas.
Simulator
Previous Years JEE Advance Questions
Paragraph for questions 1 to 3
The hydrogen-like species $\mathbf{L} \mathbf{i}^{2+}$ is in a spherically symmetric state $\mathrm{S}_{1}$ with one radial node. Upon absorbing light the ion undergoes transition to a state $\mathrm{S}_{2}$ The state $\mathrm{S}_{2}$ has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
Answer Q.10, Q.11 and Q.12 by appropriately matching the information given in the three columns of the following table.
The wave function n, l , m1 is a mathematical function whose value depends upon spherical polar coordinates $(\mathrm{r}, \theta, \phi)$ of the electron and characterized by the quantum numbers n, l and $\mathrm{m}_{1}$. Here r is distance from nucleus, is colatitude and is azimuth. In the mathematical functions given in the Table, Z is atomic number $\mathrm{a}_{0}$
is Bohr radius.
Q. The state S1 is :-
(A) 1s (B) 2s (C) 2p (D) 3s
[JEE 2010]
Ans. (B)
$\mathrm{S}_{1}=2 \mathrm{s}$
$\mathrm{S}_{2}=3 \mathrm{p}$
Q. Energy of the state $\mathrm{S}_{1}$ in units of the hydrogen atom ground state energy is :-
(A) 0.75 (B) 1.50 (C) 2.25 (D) 4.50
[JEE 2010]
Ans. (C)
$\mathrm{E}=13.6 \times \frac{3}{4}$
Q. The orbital angular momentum quantum number of the state $\mathrm{S}_{2}$ is :-
(A) 0 (B) 1 (C) 2 (D) 3
[JEE 2010]
Ans. (B)
Q. The maximum number of electrons that can have principal quantum number, n=3, and spin quantum number, ms = – 1/2, is
[JEE 2011]
Ans. 9
Q. The work function $(\phi)$ of some metals is listed below. The number of metals which will show photoelectric effect when light of 300 nm wavelength falls on the metal is : :
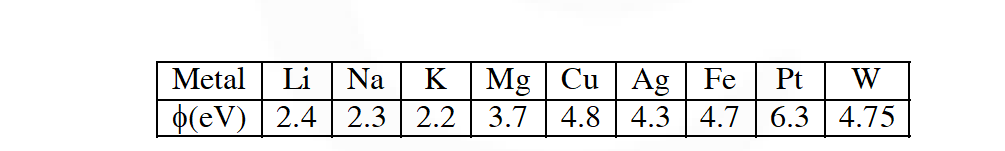[JEE 2011]
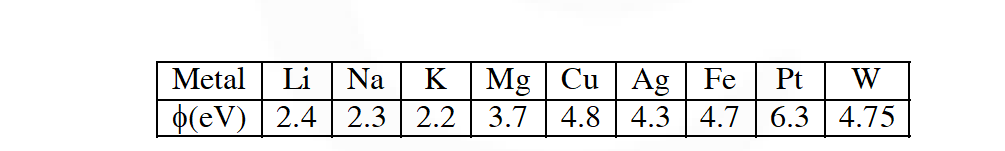[JEE 2011]
Ans. 4
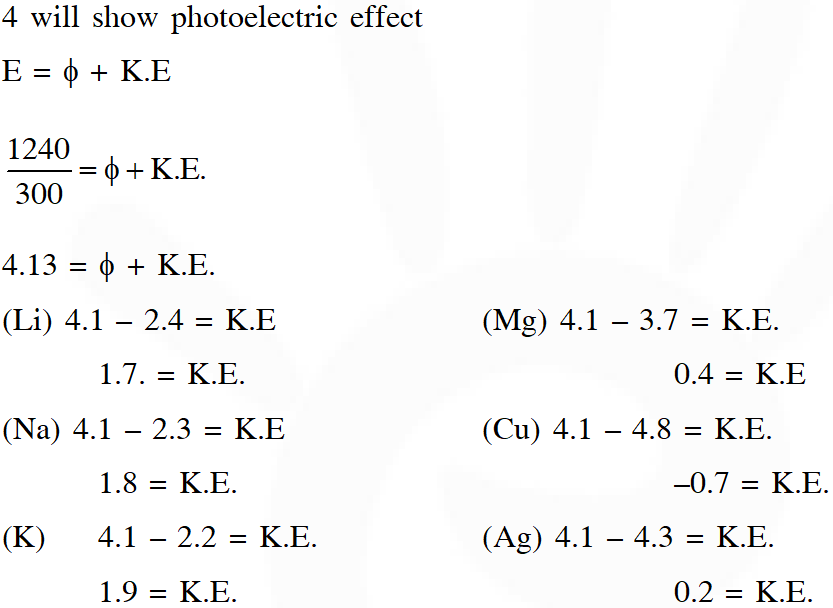
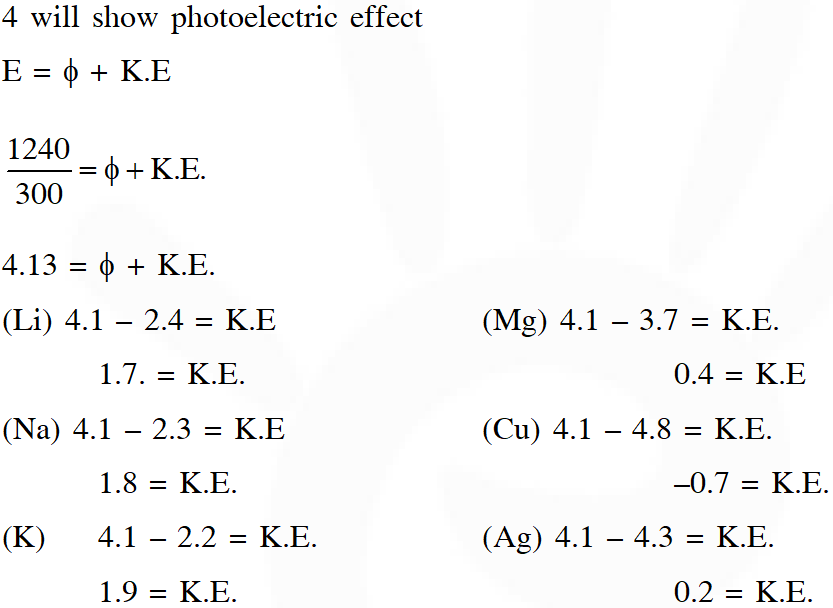
Q. The kinetic energy of an electron in the second Bohr orbit of a hydrogen atom is [$\mathrm{a}_{0}$ is Bohr radius]
$(\mathrm{A}) \frac{\mathrm{h}^{2}}{4 \pi^{2} \mathrm{ma}_{0}^{2}}$
$(\mathrm{B}) \frac{\mathrm{h}^{2}}{16 \pi^{2} \mathrm{ma}_{0}^{2}}$
(C) $\frac{\mathrm{h}^{2}}{32 \pi^{2} \mathrm{ma}_{0}^{2}}$
(D) $\frac{\mathrm{h}^{2}}{32 \pi^{2} \mathrm{ma}_{0}^{2}}$
[JEE 2012]
Ans. (C)
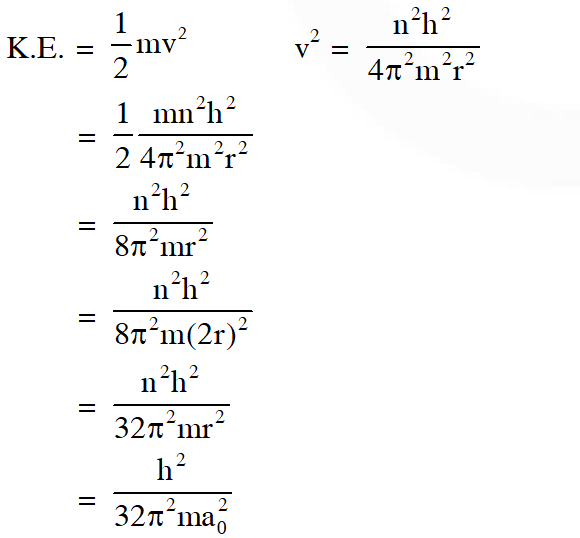
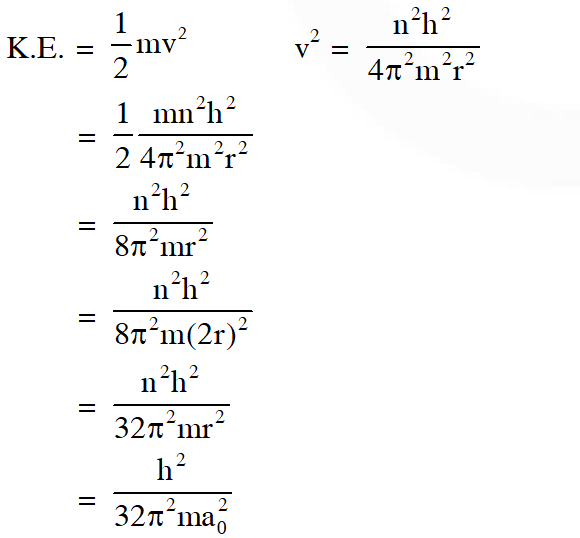
Q. The atomic masses of He and Ne are 4 and 20 a.m.u. respectively. The value of the de Broglie wavelength of He gas at $-73^{\circ} \mathrm{C}$ is "M" times that of the de Broglie wavelength of Ne at $727^{\circ} \mathrm{C}$. M is.
[JEE 2013]
Ans. (5)
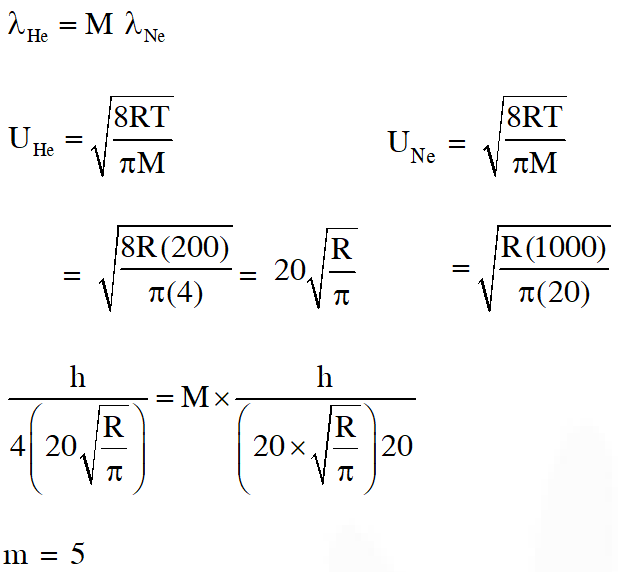
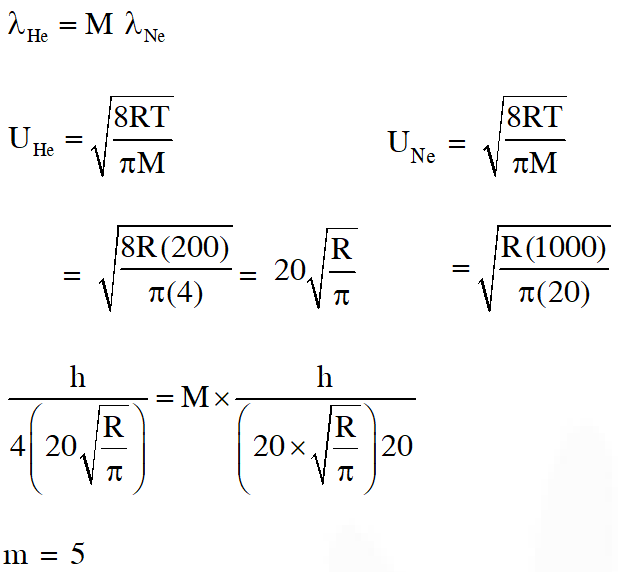
Q. In an atom, the total number of electrons having quantum numbers n = $4,\left|\mathrm{m}_{\ell}\right|=1$ and $\mathrm{m}_{\mathrm{s}}=-\frac{1}{2} \mathrm{is}$
[JEE 2014]
Ans. (6)
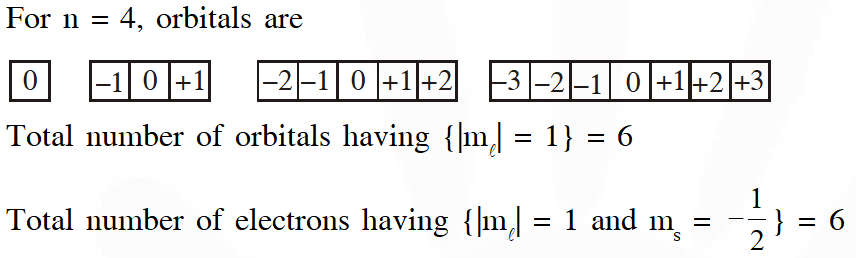
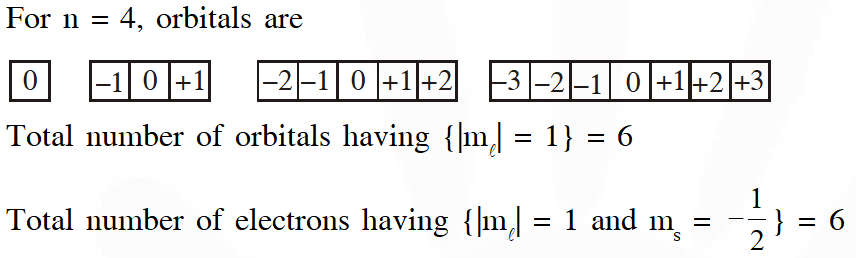
Q. P is the probability of finding the 1s electron of hydrogen atom in a spherical shell of infinitesimal thickness, dr, at a distance r from the nucleus. The volume of this shell is $4 \pi \mathrm{r}^{2} \mathrm{dr}$. The qualitative sketch of the dependence of P on r is –
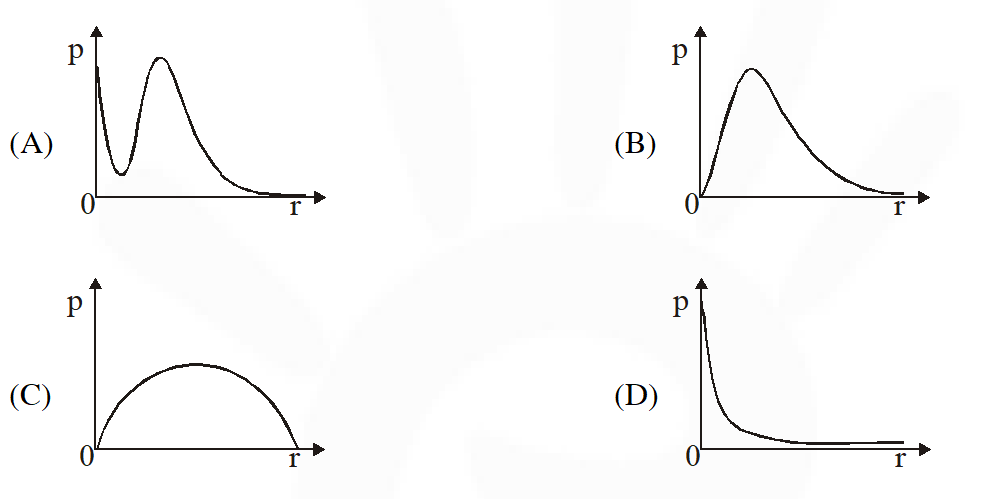[JEE Adv. 2017]
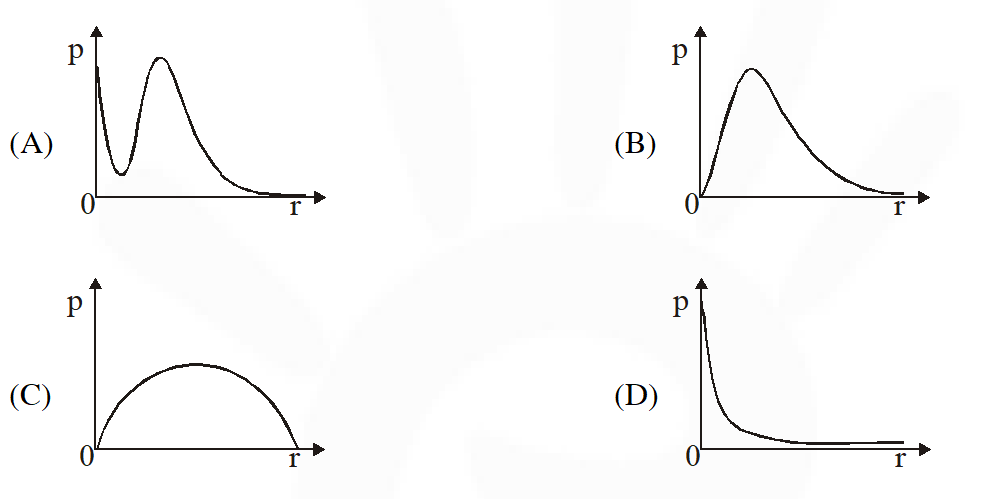[JEE Adv. 2017]
Ans. (B)
Q. For the given orbital in column 1, the only CORRECT combination for any
hydrogen - like species is :
(A) (IV) (iv) (R)
(B) (II) (ii) (P)
(C) (III) (iii) (P)
(D) (I) (ii) (S)
[JEE - Adv. 2017]
Ans. (B)
(A) (IV) (iv) (R) incorrect, because, $\mathrm{d}_{\mathrm{z}^{2}}$ has no nodal plane.
(B) (II) (ii) (P) correct, because 2s orbtial has 1 radial node.
(C) (III) (iii) (P) incorrect, because probability density for 2p at nucleus is zero.
(D) (I) (ii) (S) incorrect, because 1s orbital has no radial node.
Q. For He+ ion, the only INCORRECT combination is
(A) (II) (ii) (Q)
(B) (I) (i) (S)
(C) (I) (i) (R)
(D) (I) (iii) (R)
[JEE - Adv. 2017]
Ans. (D)
The option (D) is incorrect because in the wave function of 1s orbital , no angular function should be present.
Q. For hydrogen atom, the only CORRECT combination is
(A) (I) (iv) (R)
(B) (I) (i) (P)
(C) (II) (i) (Q)
(D) (I) (i) (S)
[JEE - Adv. 2017]
Ans. (D)
We have to select only correct combination hence, the option (D) is correct.
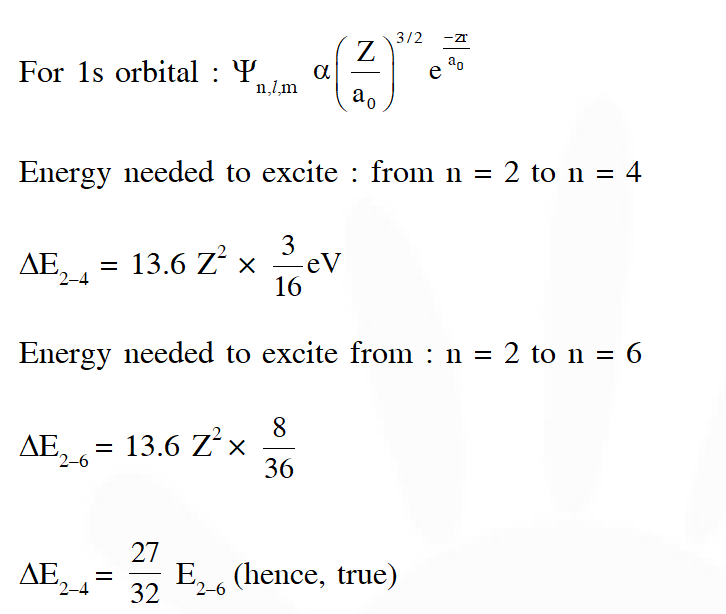
Comments
Aman Sinha
Sept. 16, 2021, 6:26 a.m.
questions the last three years i.e., 2018, 19 and 20 are not present.
so pls update this.
Anonym
Nov. 11, 2020, 10:05 p.m.
Requires some more questions for a good practice. They were too good to solve thanku
anonymous x
Nov. 2, 2020, 5:11 p.m.
this helps a lot for finding some of best questions from atomic structure :)
ARIN SINGH
Sept. 11, 2020, 2:49 a.m.
PLEASE PROVIDE PDF... U CUD PUT YOUR NAME ON THE PDF FOR COPYRIGHT ISSUES BUT PLEASE U GOTTA DO SOMETHING ABOUT THIS